
经典的状压dp
先考虑横着放 如果横着放的方案确定了 那么竖着放的也就唯一确定了
所以总方案数=横着放的方案数
但是可能我们横着放完了后 留下的空间竖着放怎么都不能放满(也就是竖着连续对的0为奇数)不合法
这个我们可以预处理
定义方程:设dp[i,j]表示前i列已经放完横木块且第i列的状态为j的总方案数
例如j=010110 则表示第二,四,五行有木块捅到后面一列去(也就是横着放的木块的头子在第i列的第2,4,5行)
转移方程:dp[i,j]+=dp[i-1,k] 其中j和k状态必须合法
合法条件:1, j&k=0 因为防止木块重合
2, 第i列合法(第i列的木块包括第i-1列捅过来的和第i列捅出去的)
初始状态dp[0,0]=1
终止状态dp[m,0](第m列不能再往后捅了)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=12;
int n,m;
ll dp[maxn][1<<(maxn-1)];
int pd[1<<(maxn-1)];
int main(){
cin>>n>>m;
while(n!=0&&m!=0){
for(int i=0;i<1<<n;i++){
int cnt=0;
pd[i]=true;
for(int j=0;j<n;j++){
if((i>>j)&1){
if(cnt&1){
pd[i]=false;
}else cnt=0;
}else cnt++;
}
if(cnt&1)pd[i]=false;
}
memset(dp,0,sizeof(dp));
dp[0][0]=1;
for(int i=1;i<=m;i++){
for(int j=0;j<(1<<n);j++){
for(int k=0;k<(1<<n);k++){
if(!(j&k)&&pd[j|k])
dp[i][j]+=dp[i-1][k];
}
}
}
cout<<dp[m][0]<<endl;
cin>>n>>m;
}
return 0;
}

这个也是很经典的一道状压dp 比上面那道要简单
设dp[i,j]表示已经走过的城市状态为i,且最后一个城市为j
初始状态 dp[1,0]=0
终止状态 dp[(1<<n)-1,n-1]
转移方程 dp[i,j]=min(dp[i,j],dp[i-(1<<j),k]+w[k][j]) 其中j和k为i状态里面互不相同的城市
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
#define inf 1e9
const int N=20;
const int M=1<<19;
int dp[M][N],w[N][N];
int n;
int main(){
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>w[i][j];
memset(dp,0x3f,sizeof(dp));
dp[1][0]=0;
for(int i=0;i<1<<n;i++)
for(int j=0;j<n;j++)
if((i>>j)&1)
for(int k=0;k<n;k++)
if(((i>>k)&1)&&k!=j)
dp[i][j]=min(dp[i][j],dp[i-(1<<j)][k]+w[j][k]);
cout<<dp[(1<<n)-1][n-1];
return 0;
}
/*
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
*/
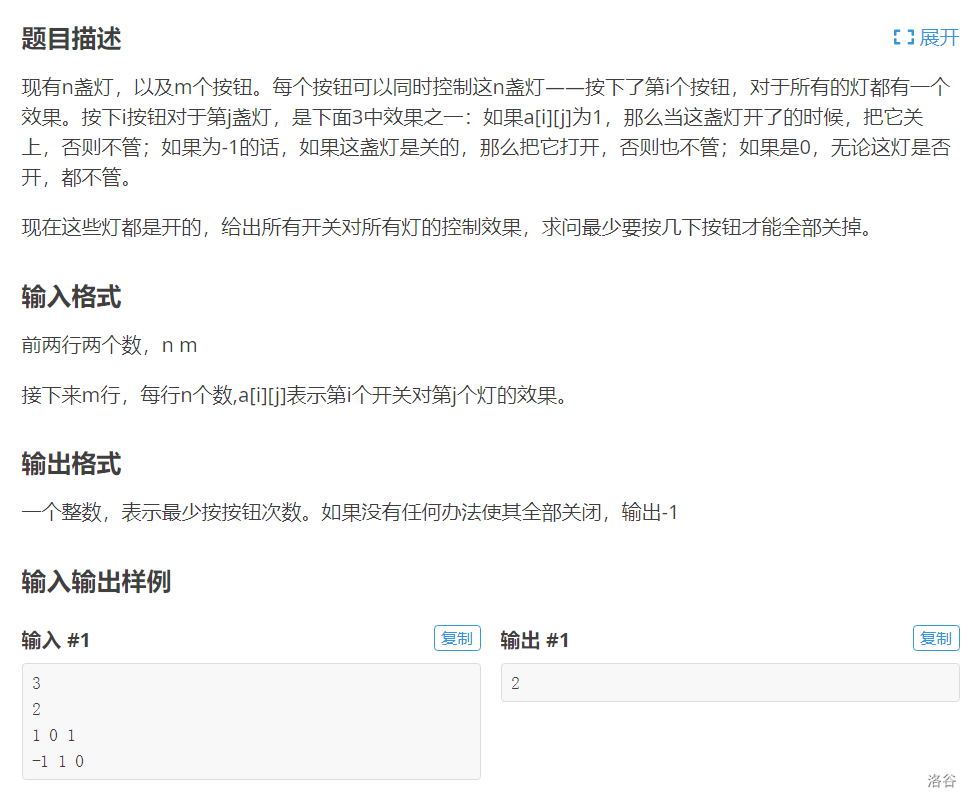
感觉这个题目放在这个专题多不好 因为正解是肯定不能用状压dp的
可以用状压 但是一定不能用dp
因为这个题目无法保证无后效性 简而言之
如果我们从大到小开始枚举状态 此时状态为 i 在按下一个按钮后状态为 j
此时 j可能大于i可能小于i 这样我们从大到小开始枚举状态的意义何在?
出这个题目的人想法很好 但是对dp理解还不够深刻
放出状压dp的code(错的但是能过)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=10;
const int maxm=105;
int n,m;
int a[maxm][maxn];
int dp[1<<(maxn+1)];
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++)
for(int j=0;j<n;j++)
cin>>a[i][j];
memset(dp,0x7f,sizeof(dp));
dp[(1<<n)-1]=0;
for(int i=(1<<n)-1;i>=0;i--){
for(int num=1;num<=m;num++){
int j=i;
for(int k=0;k<n;k++){
if(a[num][k]==1){
if((i>>k)&1)j-=(1<<k);
}else if(a[num][k]==-1){
if(!((i>>k)&1))j+=(1<<k);
}
}
dp[j]=min(dp[j],dp[i]+1);
}
}
if(dp[0]!=2139062143)
cout<<dp[0]<<endl;
else cout<<"-1"<<endl;
return 0;
}
正解就只能是bfs+状压
正确的code:
点击查看代码
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
int n, m;
int a[110][15];
bool vis[2000];
int step[2000];
queue<int> q;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
scanf("%d", &a[i][j]);
}
}
q.push((1 << n) - 1);
vis[(1 << n) - 1] = true;
while (q.size()) {
int tx = q.front(); q.pop();
if (!tx) { printf("%d", step[tx]); return 0; }
for (int i = 1; i <= m; ++i) {
int ttx = tx;
for (int j = 1; j <= n; ++j) {
if (a[i][j] == 1 && (tx & (1 << j - 1))) ttx &= ~(1 << (j - 1));//此处判断 ttx & (1 << j - 1) 亦可,因为当前位置 j 的值并未被修改
if (a[i][j] == -1 && !(tx & (1 << j - 1))) ttx |= 1 << (j - 1);
}
if (!vis[ttx]) q.push(ttx), vis[ttx] = true, step[ttx] = step[tx] + 1;
}
}
printf("-1");
return 0;
}
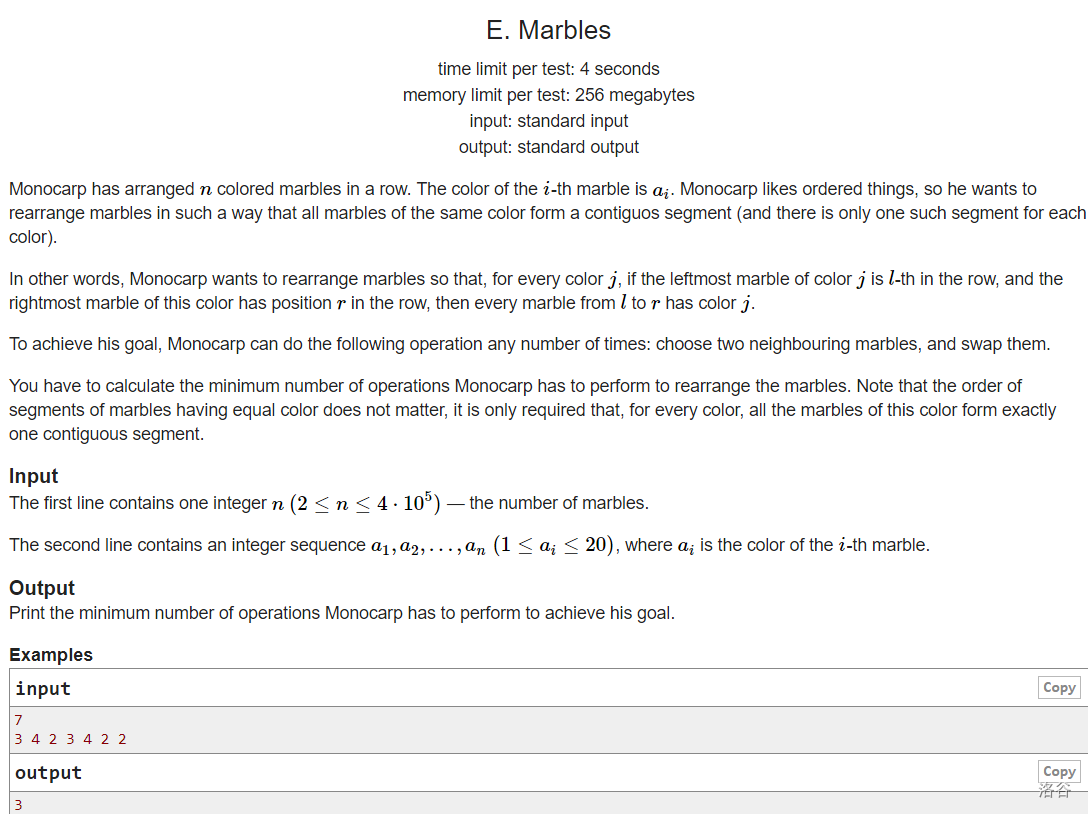
首先一看数据 状压dp跑不掉了

代码是w[i,j]是把i 全部放在 j 后面需要的步数 两种是一样的
点击查看代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#include <climits>
#include <cstdlib>
using namespace std;
const int MAXN = 4e5 + 3;
int n , a[MAXN] ;
long long w[23][23];
long long dp[1<<20+2];
long long cnt[MAXN];
int main(){
scanf( "%d" , &n );
for( int i = 1 ; i <= n ; i ++ ){
scanf( "%d" , &a[i] );cnt[a[i]-1] ++;
for( int j = 0; j < 20 ; j ++ )
w[j][a[i]-1] += cnt[j];
}
dp[0] = 0;
for( int i = 1 ; i < ( 1 << 20 ) ; i ++ ){
dp[i] = LLONG_MAX;
for( int j = 0 ; j < 20 ; j ++ ){
if( i & ( 1 << j ) ){
int k = i ^ ( 1 << j );
long long sum =0 ;
for( int l = 0 ; l < 20 ; l ++ ){
if( l != j && ( k & ( 1 << l ) ) ){
sum += w[j][l];
}
}
dp[i] = min( dp[i] , dp[k] + sum );
}
}
}
printf( "%lld" , dp[(1<<20)-1] );
}

本来找网络流24题的 但是发现这个题直接一个状压 +最短路就好了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=22;
int n,m;
int vis[(1<<maxn)],a[maxn*10],b[maxn*10],c[maxn*10],d[maxn*10];
int dis[(1<<maxn)],val[maxn];
string s;
void spfa(){
queue<int>Q;
memset(dis,0x7f,sizeof(dis));
dis[(1<<n)-1]=0;
Q.push((1<<n)-1);
while(!Q.empty()){
int u=Q.front();
Q.pop();vis[u]=0;
for(int i=1;i<=m;i++)
if((u&a[i])==a[i]&&(u&b[i])==0){
int to=((u|c[i])|d[i])^c[i];
if(dis[to]>dis[u]+val[i]){
dis[to]=dis[u]+val[i];
if(!vis[to]){
vis[to]=1;
Q.push(to);
}
}
}
}
if(dis[0]==dis[(1<<maxn)-1])
cout<<0<<endl;
else
cout<<dis[0]<<endl;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>val[i]>>s;
for(int j=0;j<n;j++)
if(s[j]=='+')a[i]|=(1<<j);
else if(s[j]=='-')b[i]|=(1<<j);
cin>>s;
for(int j=0;j<n;j++)
if(s[j]=='-')c[i]|=(1<<j);
else if(s[j]=='+')d[i]|=(1<<j);
}
spfa();
return 0;
}