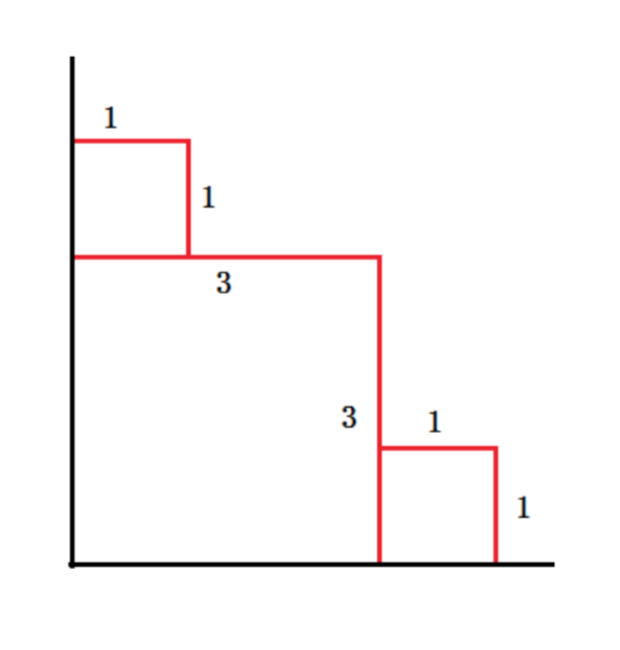
There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.
Input
The first line is the number of waves n(n le 50000)n(n≤50000).
The next nn lines,each contains two numbers xx yy ,( 0 < x0<x , y le 10000000y≤10000000 ),the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 le i1≤i , j le nj≤n ,x_i le x_jxi≤xj and y_i le y_jyi≤yj don't set up at the same time.
Output
An Integer stands for the answer.
Hint:
As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10
样例输入复制
3 1 4 4 1 3 3
样例输出复制
10
题目来源
题意:
每次给一个点 与原点画一个矩形 后面的矩形会覆盖前面的矩形
求所有露在外面的矩形的边的长度之和
思路:
线段树 将横线和竖线分开
以横线为例
从后往前 当前这条横线对结果的贡献 = 本身的长度 - 被之前的(也就是后来的矩形)遮掉的长度
后来的矩形的横线这有在这条横线之上才会对这条横线有影响
树存放当前y坐标到无穷大之间 横线的最大长度
首先离散化所有的xy坐标
从后往前处理点 查询当前y坐标之上的横线最大长度
结果加上当前横线长度-查询所得
更新y节点的值为当前横线长度
初始化树的节点都是0 做一个更新一个 build都不需要
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
#include<set>
//#include<bits/stdc++.h>
#define inf 0x7f7f7f7f7f7f7f7f
using namespace std;
typedef long long LL;
const int maxn = 50005;
int n;
struct node {
int x, y;
}nodes[maxn];
map<int, int> newx, newy;//离散化xy坐标
set<int>xx, yy;
set<int>::iterator it;
int treex[maxn << 2], treey[maxn << 2];
void pushupx(int rt)
{
treex[rt] = max(treex[rt << 1], treex[rt << 1 | 1]);
}
void pushupy(int rt)
{
treey[rt] = max(treey[rt << 1], treey[rt << 1 | 1]);
}
void updatex(int x, int val, int l, int r, int rt)
{
if (l == r) {
treex[rt] = val;
return;
}
int m = (l + r) / 2;
if (x <= m) {
updatex(x, val, l, m, rt << 1);
}
else {
updatex(x, val, m + 1, r, rt << 1 | 1);
}
pushupx(rt);
}
void updatey(int x, int val, int l, int r, int rt)
{
if (l == r) {
treey[rt] = val;
return;
}
int m = (l + r) / 2;
if (x <= m) {
updatey(x, val, l, m, rt << 1);
}
else {
updatey(x, val, m + 1, r, rt << 1 | 1);
}
pushupy(rt);
}
LL queryx(int L, int R, int l, int r, int rt)
{
if (L <= l && R >= r) {
return treex[rt];
}
int m = (l + r) / 2;
LL ans = 0;
if (L <= m) {
ans = max(ans, queryx(L, R, l, m, rt << 1));
}
if (R > m) {
ans = max(ans, queryx(L, R, m + 1, r, rt << 1 | 1));
}
return ans;
}
LL queryy(int L, int R, int l, int r, int rt)
{
if (L <= l && R >= r) {
return treey[rt];
}
int m = (l + r) / 2;
LL ans = 0;
if (L <= m) {
ans = max(ans, queryy(L, R, l, m, rt << 1));
}
if (R > m) {
ans = max(ans, queryy(L, R, m + 1, r, rt << 1 | 1));
}
return ans;
}
void init()
{
memset(treex, 0, sizeof(treex));
memset(treey, 0, sizeof(treey));
newx.clear();
newy.clear();
xx.clear();
yy.clear();
}
int main()
{
while (scanf("%d", &n) != EOF) {
init();
for (int i = 0; i < n; i++) {
scanf("%d%d", &nodes[i].x, &nodes[i].y);
xx.insert(nodes[i].x);
yy.insert(nodes[i].y);
}
int cntx = 1, cnty = 1;
for (it = xx.begin(); it != xx.end(); it++) {
newx[*it] = cntx++;
}
cntx--;
for (it = yy.begin(); it != yy.end(); it++) {
newy[*it] = cnty++;
}
cnty--;
LL ans = 0;
//buildx(1, cnty, 1);
//buildy(1, cntx, 1);
for (int i = n - 1; i >= 0; i--) {
int nowy = newy[nodes[i].y], nowx = newx[nodes[i].x];
LL resx = queryx(nowy + 1, cnty, 1, cnty, 1), resy = queryy(nowx + 1, cntx, 1, cntx, 1);
ans += nodes[i].x - resx + nodes[i].y - resy;
updatex(nowy, nodes[i].x, 1, cnty, 1);
updatey(nowx, nodes[i].y, 1, cntx, 1);
}
printf("%lld
", ans);
}
return 0;
}