F. Trig Function

样例输入
2 0 2 1 2 2
样例输出
998244352 0 2
找啊找啊找数列和论文。cosnx可以用切比雪夫多项式弄成(cosx)的多项式,然后去找到了相关的公式:


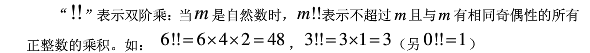
然后写个快速幂预处理啥的,很快就解决了~

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define mod 998244353 6 using namespace std; 7 LL jc[10010],djc[10010]; 8 LL n,m,k,ans; 9 LL quick_pow(LL x,LL n) 10 { 11 LL res=1; 12 x=(x%mod+mod)%mod; 13 while(n) 14 { 15 if(n&1) 16 res=res*x%mod; 17 x=x*x%mod; 18 n>>=1; 19 } 20 return res; 21 } 22 23 void init() 24 { 25 jc[1]=jc[0]=1; 26 for(int i=2;i<=10000;i++) 27 jc[i]=(jc[i-1]*i)%mod; 28 djc[10000]=quick_pow(jc[10000],mod-2); 29 for(int i=9999;i>=1;i--) 30 djc[i]=djc[i+1]*(i+1)%mod; 31 djc[0]=1; 32 return ; 33 } 34 int main() 35 { 36 init(); 37 while(scanf("%lld%lld",&n,&m)!=EOF) 38 { 39 if(m>n || m<0 || (n-m)%2!=0) 40 { 41 printf("0 "); 42 continue; 43 } 44 ans=(n-m)/2%2==1?-1:1; 45 ans=(ans*djc[m]*n%mod+mod)%mod; 46 if(n-m<=n+m-2) 47 for(LL i=n-m+2;i<=n+m-2;i+=2) 48 ans=ans*(i%mod)%mod; 49 else 50 for(LL i=n-m;i>n+m-2;i-=2) 51 ans=ans*quick_pow(i,mod-2)%mod; 52 printf("%lld ",ans); 53 } 54 return 0; 55 }
E。 Maximum Flow

样例输入
2
样例输出
1
这题可以用最大流最小割推推,但我~找规律的2333。
首先是2^k的n(默认n--了),那么所有的从0出来的流都能到达终点,也就是流量为(n+1)*n/2。然后写个最大流打个表,然后将i和i-1作差。可以发现在2^k~2^(k+1)的数中,差为2(2^0+1)每隔2个出现,差为5(2^2+1)每隔4个出现,17(2^4+1)每隔8个出现。。。依此类推。然后你懂得~。

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define LL long long 4 #define mod 1000000007 5 using namespace std; 6 LL quick_pow(LL x, LL n) { 7 LL res = 1; 8 x=(x%mod+mod)%mod; 9 while(n) { 10 if(n&1) 11 res=res*x% mod; 12 n >>=1; 13 x =x*x% mod; 14 } 15 return res; 16 } 17 int main() 18 { 19 LL n,m,q,l,ans,k,kk; 20 int t; 21 while(scanf("%lld",&n)!=EOF) 22 { 23 t=0; 24 n--; 25 m=n; 26 while(m) 27 { 28 t++; 29 m>>=1; 30 } 31 q=1; 32 m=(q<<(t-1)); 33 ans=(m%mod)*((1+m)%mod)%mod; 34 ans=ans*quick_pow(2,mod-2)%mod; 35 n-=m; 36 kk=1; 37 k=2; 38 while(k<=n+kk) 39 { 40 ans=(ans%mod+(((n+kk)/k)%mod)*((kk%mod)*(kk%mod)%mod+1)%mod)%mod; 41 if(k==LLONG_MAX) 42 break; 43 kk=k; 44 k<<=1; 45 } 46 printf("%lld ",ans); 47 } 48 return 0; 49 }
C.Sum

样例输入
1 1
样例输出
89999999999999999999999999
输入啥都输出233个9就行了。k个9无论乘多少数位和仍是k*9。

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 using namespace std; 6 int main() 7 { 8 LL n,m,k; 9 int T; 10 scanf("%d",&T); 11 while(T--) 12 { 13 scanf("%lld",&n); 14 for(int i=1;i<=233;i++) 15 printf("9"); 16 printf(" "); 17 } 18 return 0; 19 }
B.Coin

样例输入
2 2 1 1 3 1 2
样例输出
500000004 555555560
23333,n重伯努利实验概率分布题。
设q=1-p,p为事件概率。
Y为出现偶数次的概率。
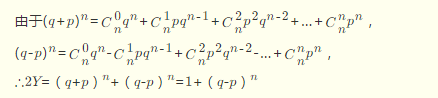
所以Y=(1+(q-p)^n)/2,求个逆元啥的,快速幂啥的就能做出来了。

1 #include<bits/stdc++.h> 2 #define LL long long 3 #define mod 1000000007 4 using namespace std; 5 LL quick_pow(LL x, LL n) { 6 LL res = 1; 7 x=(x%mod+mod)%mod; 8 while(n) { 9 if(n&1) 10 res=res*x% mod; 11 n >>=1; 12 x =x*x% mod; 13 } 14 return res; 15 } 16 int main() 17 { 18 LL p, q; 19 LL n; 20 int t; 21 scanf("%d", &t); 22 while(t --) { 23 scanf("%lld%lld%lld",&p, &q, &n); 24 LL a=quick_pow(p,mod-2); 25 a=(a*2*q)%mod; 26 a=(1-a+mod)%mod; 27 a=quick_pow(a,n)%mod; 28 a=(a+1)%mod; 29 LL b=quick_pow(2,mod-2)%mod; 30 a=(a*b)%mod; 31 printf("%lld ", (a%mod+mod)%mod); 32 } 33 }
