声明:
本题解借鉴了@Heartlessly(luogu UID=32139)的内容
题目大意:
每只牛对于每个牛棚有一个差评值,现在分配牛棚,使得所有牛的最大差评值与最小差评值的差最小,求这个值。
正文:
因为题目中有提到过每个牛棚的限度,也就是说我们可以用网络瘤来求解。
样例图:
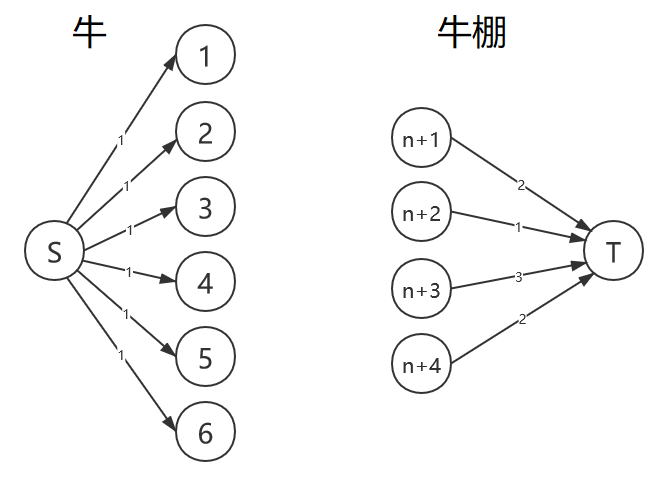
牛棚编号要加上(n)因为牛那边已经用过
接着怎么办?我们考虑到二分答案。
那我们先想一想最大差评值与最小差评值的差最大是多少,因为最大差评值最大(=b), 最小差评值最小(=1),那么最大差评值与最小差评值的差最大是(b-1)
我们可以再([1,b])中找到我们的答案。
假设我们二分到(x)(最大差评值与最小差评值的差),最小差评值(=i),那么最大差评值(=i+x-1)。先把上图情况存入邻接表,我们肯定不能直接把牛连到所有牛棚只能连部分的。既然二分到(x)的最小差评值(=i),最大差评值(=i+x-1),那么每头牛就只能连它第(i)个到第((i+x-1))个牛棚。
做完连一连后,跑一遍最大流,毕竟我们本身就是(n)头牛,如果最大流不是(n)那么方案就是不可行的。
代码:
bool check(int x)
{
for (int i = 1; i + x - 1 <= b; i++)
{
memset(head, 0, sizeof(head));
tot = 0;
s = n + b + 1, t = n + b + 2;
for (int j = 1; j <= n; j++) Add(s, j, 1); //连成上图
for (int j = 1; j <= b; j++) Add(j + n, t, v[j]);
for (int j = 1; j <= n; j++)
for (int k = i; k <= i + x - 1; k++)
Add(j, like[j][k] + n, 1); //连第i个到第(i+x-1)个牛棚
int ans = dinic();
if(ans == n) return 1; // 网络瘤
}
return 0;
}
int main()
{
scanf("%d%d", &n, &b);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= b; j++)
scanf("%d", &like[i][j]); //like[i][j] 表示第i只牛差评度为j的牛棚
for (int j = 1; j <= b; j++)
scanf("%d", &v[j]); // v[i] 表示第i个牛棚的限度
int l = 1, r = b, mid, ans = 0;
while(l <= r) //二分开始
{
mid = (l + r) >> 1;
if(check(mid))
{
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
printf("%d", ans);
return 0;
}