A
略
B
略
C(轮廓线dp)
题意:


分析:
如果以(i,j)为右下角考虑设计dp,那么会需要用到多余的状态,这样状态就很爆炸了
仍旧考虑轮廓线dp,维护一个格子上的轮廓线的m个状态,考虑从dp(i,j)转移到一个dp(i,j+k)
即以(i,j)为矩形的左下角去枚举转移,这样只需要轮廓线上的状态就满足了
时间复杂度O(nm*(2^m)*k)
D(hash/SAM)
题意:

分析:
对于每个s建立SAM,t在上面查询,这是经典问题,时间复杂度是O(26len),但常数比较大被卡常了
可以用hash来解决,时间复杂度是O(lenlog|T|)的,但常数比SAM要小,不过因为很长,所以出现冲突的概率就很大,就要用双hash
E(多项式)
题意:

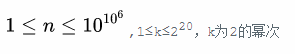
分析:
对于$ans_t$,本质上就是多项式$(1+x)^n$的展开式中所有模k余t的项的系数和,从而可以看做是n个长度为k的多项式(1+x)的循环卷积的第t项的系数
因为k是2的幂次,所以k|(998244353-1),所以可以求出单位根在对应的0~k-1次幂下原本多项式的点值,然后NTT插出循环卷积的多项式即可
注意到n很大,但我们只需要求类似$a^n % P$,指数对P-1取模不会改变结果
F(分治NTT)
题意:

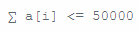
分析:
首先分析获胜的概率
若只考虑一堆,那么先手是赢还是输这取决于几步把这个堆取完
奇数次把这个堆取完的方案数是C(num-1,0)+C(num-1,2)+C(num-1,4)+.....
偶数次把这个堆取完的方案数是C(num-1,1)+C(num-1,3)+C(num-1,5)+.....
这两个值是相同的,所以获胜概率其实是相同的
考虑所有堆,获胜概率应该也是相同的,所以答案是1/2
但要考虑特殊情况,那就是若所有堆都是1,那么概率要么是0,要么是1,这取决于堆数的奇偶性
考虑第二个问题,即有多少种取的方法使得先手获胜,同样,这也只是取决于取完所有石子的步数的奇偶性
f[i][j]表示前i堆j次操作完的方案数,很显然有这样的式子f[i][j]=Σf[i-1][j-k]*C(a[i]-1,k-1)*C(j,k) (1<=k<=a[i])
后面这个推一推可以用NTT优化
但是这题n的范围没有给,所以很可能出现这种情况:25000 1 1 1 1 .....,这样时间复杂度会降至O(len^2log(len)),会TLE
这个式子的本质是这样的:f(i)=f(i-1)与h(i)的卷积
这个东西其实就是h(1) h(2) h(3) ... h(n)的卷积,分治NTT解决就行了,时间复杂度$O(lenlog^2len)$
具体实现的时候也不需要递归分治,只需要把h(1) h(2) h(3) ... h(n)丢到一个队列里,然后每次取出队首进行卷积,卷积结果丢到队尾就行了