倏逝波又叫消逝波或者隐失波,其幅值随与分界面相垂直的深度的增大而呈指数形式衰减。
消逝波(又称表面波, 英文: Evanescent field)是指当光波在两种介质产生全反射时发生的光学现象。
定义:
一般来讲, 当光波从光密介质入射到光疏介质时,如果入射角大于临界角会产生全反射现象。 此时有光波虽然不能穿过两种介质的临界面, 但沿着临界面平行的方向会产生光波,其电场及磁场的复振幅随着远离临界面的距离的增大而呈现指数级的减小趋势,这部分光波被称为消逝波,或称为表面波。
理论解释:
研究发现,物体受光波照射后,离开物体表面的光波分为两种成份:一部分光向远方传播,这是传统光学显微镜能接收的信息;而另一部分光波只能沿物体表面传播,一旦离开表面就很快衰减。从几何光学的角度来看,当发生全反射时,光会在玻璃界面上完全反射而不进入液体溶液中。实际上,由于波动效应,有一部分光的能量会穿过界面渗透到溶液中,平行于界面传播。这部分光就是所谓的隐失波 。
隐失波还有另外一种解释:对于一个有限大小的物体,其空间频谱是无限延伸的。其中低频分量为传输波分量,高频分量为隐失波分量。即隐失波分量反映物体的细节信息,通过恢复物体的隐失波分量可以实现物体的亚波长成像。
全反射时,光波不是绝对在界面上被反射回第一介质,而是透入第二介质大约一个波长的深度,并沿着界面流过波长量级距离后重新返回第一介质,沿着反射光方向射出。这个沿着第二介质表面流动的波称为隐失波,曾称倏逝波。隐失波离开表面的衰减是呈指数形式的。
方程推导:
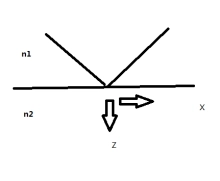
由于有n1sinθi=n2sinθt,且为全反射,因此可知sinθt>1,cosθt=√(1-sin2θt)=jΓ,其中j为虚数单位,Γ=√[(n1sinθi/n2)2-1],Γ为一实数。
设入射光波的波动方程为Ei=Eiosexp[j(ki·r-ωt)],折射光波方程为Et=Eiosexp[j(kt·r-ωt)],对于非全反射情况,由界面两侧的B,D,E,H的条件,可以推出ki·r=kt·r=kxx+kyy+kzz,由于r为任意,从而得到kisinθi=ktsinθt,(波矢k=2π/λ=2πnν/c,所以这也就是从电磁波角度的光折射定律的推导,可以参考相关书籍,这里不展开)
回到全反射情形,由于入射面为y=0平面,矢积ki·r=kixsinθi+kizcosθi=kixx+kizz,kt·r=ktxsinθt+ktzcosθt=kixsinθi+jktzΓ=kixx+jktzΓ,代入折射光波方程Et=Eiosexp[j(kixx+jktzΓ-ωt)]=Eiosexp(-ktzΓ)exp[j(kixx-ωt)],可见Et的幅值与z呈指数递减,而相位则只与x有关,因此隐失波一般不是横波。