【原】特征/SVD分解（图像压缩）/PCA降维简介

说明：实际上EVD（特征分解）是SVD的一种特殊情况；逆是伪逆的特殊情况？，这在最小二乘当中有应用。

在“8点法”求解本质矩阵当中会有SVD分解，在3D到3D空间转换中，算法icp有SVD解法。SVD作为一种分解矩阵的方法，

有着广泛应用。

一、特征分解（手写word截图）

%% Matlab验证代码
a=[1 2 3;2 1 3;3 3 6]
[x,y]=eig(a) %% x矩阵每一列代表 lamda123 对应的特征向量
diag(y) %% y矩阵的对角元素是对应特征值lamda123

二、 SVD分解和图像压缩

数学概念；参考：  https://www.cnblogs.com/xugenpeng/p/4839336.html?from=singlemessage&isappinstalled=0

                 

A = [1 2; 0 0; 0 0]
[U, S, V] = svd(A);

和手动计算结果一致。

图像压缩实例

#include<iostream>
using namespace std;

#include<opencv2/opencv.hpp>
using namespace cv;

void printMat(Mat& matrix)
{
    for (int j = 0; j < matrix.rows; j++)
    {
        for (int i = 0; i < matrix.cols; i++)
        {
            cout << matrix.ptr<double>(j)[i] << ", ";
        }
        cout << endl;
    }
    cout << endl;
}

// input:  image : ...
//         radio : 压缩比率
// ouput:  Mat : 压缩后的灰度图
Mat compressJPG(Mat image, double radio)
{
    SVD svd_1st(image, SVD::MODIFY_A);
    Mat W_ = Mat::zeros(svd_1st.w.rows, svd_1st.w.rows, CV_64F);

    // 压缩比例：radio = m*n/(r*(m+n+1))
    // r = m*n / (radio*(m+n+1))
    double m = double(image.rows);
    double n = double(image.cols);
    double r = m * n/(radio*(m + n + 1));
    int r_ = int(r);
    if (r_  >= svd_1st.w.rows)
    {
        cout << "errors in setting radio!" << endl;
        return Mat();
    }
    //for (int i = 0; i < svd_1st.w.rows; i++)
    for (int i = 0; i < r_; i++)
    {
        W_.ptr<double>(i)[i] = svd_1st.w.ptr<double>(i)[0];
    }

    Mat image_compressed = svd_1st.u * W_ * svd_1st.vt;
    image_compressed.convertTo(image_compressed, CV_8U);
    return image_compressed;
}

int main()
{
    // <1> test SVD API of opencv 
    Mat A = (Mat_<double>(3, 2) << 1, 2, 0, 0, 0, 0);
    cout << "原矩阵 A = " << endl;
    printMat(A);
    Mat W, U, Vt;
    SVD::compute(A,W,U,Vt, SVD::MODIFY_A);

    cout << "奇异值矩阵 W =" << endl;
    printMat(W);
    cout << "左奇异值矩阵 U =" << endl;
    printMat(U); //U是 3X2. rank(U) = 2; to save space, U has's 2 cols.
    cout << "右奇异值矩阵（自动转置） Vt =" << endl;
    printMat(Vt);

    // <2> recover the matrix 'A'
    Mat W_ = Mat::zeros(W.rows, W.rows, CV_64F); // 构建奇异值（方）矩阵，不保留0行 
    for (int i = 0; i < W.rows; i++)
    {
        W_.ptr<double>(i)[i] = W.ptr<double>(i)[0];
    }
    Mat A_ = U*W_*Vt;
    cout << "恢复之后：" << endl;
    printMat(A_);

    //*******************************************************************************************************
    // 压缩图像例子
    // 假设原矩阵 A 是 m x n;奇异值个数为r（也就是rank(A) = r）
    // 那么压缩比例：radio = m*n/(r*(m+n+1))
    // 分母分别是 r*m : 左奇异矩阵元素个数； r*n : 右奇异矩阵元素个数；  r: 奇异值矩阵元素个数

    Mat image = imread("2.jpg", 0);
    imshow("image", image);
    image.convertTo(image, CV_64F);

    Mat image_1st = compressJPG(image, 0.6);
    if (!image_1st.empty())
    {
        imshow("radio = 0.6", image_1st);
        imwrite("image_1st.jpg", image_1st);
    }
    
    Mat image_2st = compressJPG(image, 1);
    if (!image_2st.empty())
    {
        imshow("radio = 1", image_2st);
        imwrite("image_2st.jpg", image_2st);
    }

    Mat image_3st = compressJPG(image, 3);
    if (!image_3st.empty())
    {
        imshow("radio = 3", image_3st);
        imwrite("image_3st.jpg", image_3st);
    }
    
    Mat image_4st = compressJPG(image, 5);
    if (!image_4st.empty())
    {
        imshow("radio = 5", image_4st);
        imwrite("image_4st.jpg", image_4st);
    }

    Mat image_5st = compressJPG(image, 7);
    if (!image_5st.empty())
    {
        imshow("radio = 7", image_5st);
        imwrite("image_5st.jpg", image_5st);
    }

    Mat image_6st = compressJPG(image, 9);
    if (!image_6st.empty())
    {
        imshow("radio = 9", image_6st);
        imwrite("image_6st.jpg", image_6st);
    }

    Mat image_7st = compressJPG(image, 20);
    if (!image_7st.empty())
    {
        imshow("radio = 20", image_7st);
        imwrite("image_7st.jpg", image_7st);
    }

    waitKey(0);    
    return 1;
}

 这里比率设置不正确，返回一个提示!

可以看到压缩比率越大，图像失真越明显。

可以看到压缩比率增大，图像体积变小，别小看一张图减小十几kb大小，对于视频网站来讲.......毋庸置疑，开源节流！

楼主不是专门研究图像压缩的，就不深究了，据说微信能将一张由iphone拍的照片（10Mb左右）压缩到几百kb，图像依然很清晰！

三、PCA降维

参考：https://zhuanlan.zhihu.com/p/21580949

给出PCA的一般数学步骤：

顺便给出一道例题：

依据上述步骤，我们来解一道题

投影后如图；

（顺便：如果用 特征值 2/5 对应的特征向量作为矩阵P；

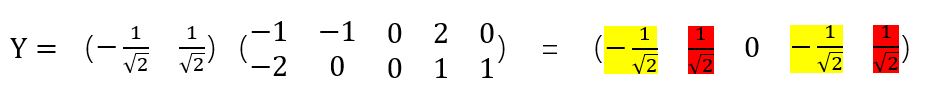
可以看到，如果映射到一维数轴上，是有信息丢失的。你看下图，是主城成分，二维数据映射到一维空间，）

  工程上，数据维度太高，其中又有许多冗余成分；这样处理起来效率不高。这时候，我们可以对数据经行降维。

PCA，即：主成成分分析，回想SVD分解图像压缩实例。我们保留最大的几个奇异值，就可以压缩数据的同时，还能最大化减少信息的损失。同理，通过多种线性变换，我们可以将原始数据降维，往往原始数据对应的协方差矩阵的多个奇异值/特征值中，将最大的几个值所对应的特征向量作为线性变换矩阵，可以起到降维作用。如上图，我们便是将最大特征值 2 对应的特征向量 作为矩阵P（P是什么？看上述PCA计算步骤）。你可以看看参考链接，另外为了更好理解PCA，你可以去看看有关PCA的应用，参考：

https://blog.csdn.net/HLBoy_happy/article/details/77146012