P2615 神奇的幻方
题目描述
幻方是一种很神奇的N*N矩阵:它由数字1,2,3,……,N*N构成,且每行、每列及两条对角线上的数字之和都相同。
当N为奇数时,我们可以通过以下方法构建一个幻方:
首先将1写在第一行的中间。
之后,按如下方式从小到大依次填写每个数K(K=2,3,…,N*N):
1.若(K−1)在第一行但不在最后一列,则将K填在最后一行,(K−1)所在列的右一列;
2.若(K−1)在最后一列但不在第一行,则将K填在第一列,(K−1)所在行的上一行;
3.若(K−1)在第一行最后一列,则将K填在(K−1)的正下方;
4.若(K−1)既不在第一行,也不在最后一列,如果(K−1)的右上方还未填数,则将K填在(K−1)的右上方,否则将K填在(K−1)的正下方。
现给定N请按上述方法构造N*N的幻方。
输入输出格式
输入格式:
输入文件只有一行,包含一个整数N即幻方的大小。
输出格式:
输出文件包含N行,每行N个整数,即按上述方法构造出的N*N的幻方。相邻两个整数之间用单个空格隔开。
输入输出样例
3
8 1 6 3 5 7 4 9 2

#include <bits/stdc++.h> using namespace std; int mp[55][55]; int main() { //freopen("magic.in","r",stdin); //freopen("magic.out","w",stdout); int n; scanf("%d",&n); mp[1][n/2+1] = 1; int x = 1, y = n/2+1, k =2; while(k != n*n+1){ if(x==1&&y!=n) x=n, y += 1; else if(y==n&&x!=1) x -=1, y=1; else if(x==1&&y==n) x+=1; else if(x!=1&&y!=n) if(!mp[x-1][y+1])x-=1, y+=1; else x += 1; mp[x][y] = k; k++; } for(int i = 1; i <= n; i++){ for(int j = 1; j <= n; j++) printf("%d ",mp[i][j]); cout<<endl; } return 0; }
P2661 信息传递
题目描述
有n个同学(编号为1到n)正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息,但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入输出格式
输入格式:
输入共2行。
第1行包含1个正整数n表示n个人。
第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i
的同学的信息传递对象是编号为Ti的同学,Ti≤n且Ti≠i
数据保证游戏一定会结束。
输出格式:
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
输入输出样例
说明
样例1解释
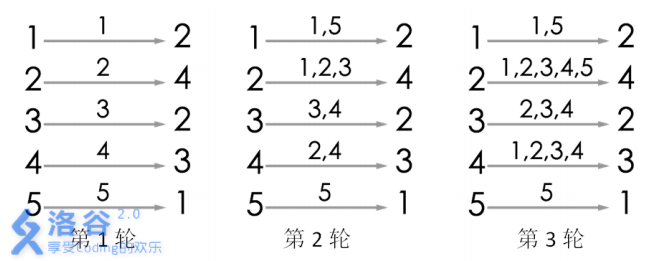
游戏的流程如图所示。当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自
己的生日,所以答案为 3。当然,第 3 轮游戏后, 2 号玩家、 3 号玩家都能从自己的消息
来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
题解:找大小大于1的最小强连通分量;

#include <bits/stdc++.h> using namespace std; const int M = 200005, inf = 100000008; int dfn[M], low[M], h[M], tot, idx, dep, ins[M], sccnt, scc[M]; int ans = inf; stack <int> s; struct edge{int v,nxt;}G[M*2]; void add(int u, int v){G[++tot].v = v, G[tot]. nxt = h[u], h[u] = tot;} int tarjan(int u){ dfn[u] = low[u] = ++idx; s.push(u); ins[u] = 1; for(int i = h[u]; i; i = G[i].nxt){ int v = G[i].v; if(!dfn[v]){ tarjan(v); low[u] = min(low[u], low[v]); } else if(ins[v]) low[u] = min(dfn[v], low[u]); } if(low[u] == dfn[u]){ int siz = 0; sccnt++; while(1){ int t = s.top();s.pop(); siz++; ins[t] = 0; scc[t] = sccnt; if(t == u)break; } if(siz > 1)ans = min(ans, siz); } } int main() { //freopen("message.in","r",stdin); //freopen("message.out","w",stdout); int n; scanf("%d",&n); for(int i = 1; i <= n; i++){ int v; scanf("%d",&v); add(i, v); } for(int i = 1; i <= n; i++) if(!dfn[i])tarjan(i); cout<<ans<<endl; return 0; }
或者并查集打标记;

#include<bits/stdc++.h> using namespace std; const int M = 200005; int f[M], to[M], h[M], vis[M], ans = 100000008; int find(int x){ return f[x] = f[x] == x ? x : find(f[x]); } void merge(int u, int v){ int x = find(u), y = find(v); f[y] = x; } int dfs(int u, int dep){ vis[u]=1; h[u]=dep; if(!vis[to[u]]) dfs(to[u], dep+1); else { int t = h[u] - h[to[u]] + 1; ans = min(ans, t); } } int main(){ int n; scanf("%d",&n); for(int i = 1; i <= n; i++)f[i] = i; for(int i = 1; i <= n; i++){ scanf("%d",&to[i]); if(find(i) != find(to[i])) merge(i, to[i]); else { memset(vis, 0, sizeof(vis)); dfs(i, 1); } } printf("%d ",ans); }
这道题出度为1是关键,开始搞成出度>1想了半天
P2668 斗地主
题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
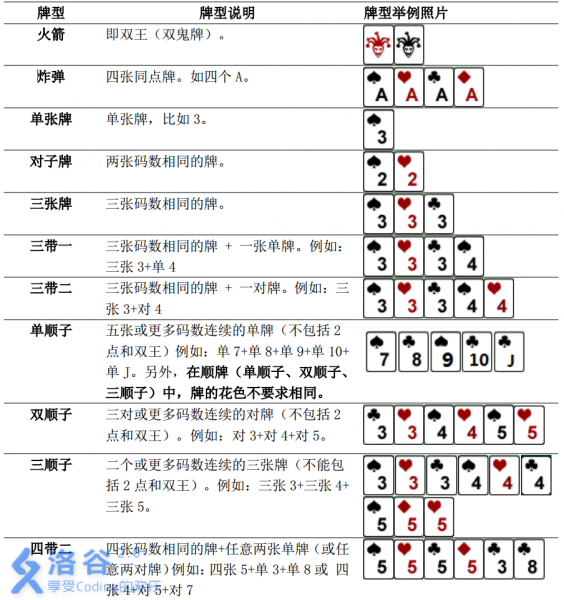
输入输出格式
输入格式:
第一行包含用空格隔开的2个正整数T和n,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出格式:
共T行,每行一个整数,表示打光第i手牌的最少次数。
输入输出样例
说明
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
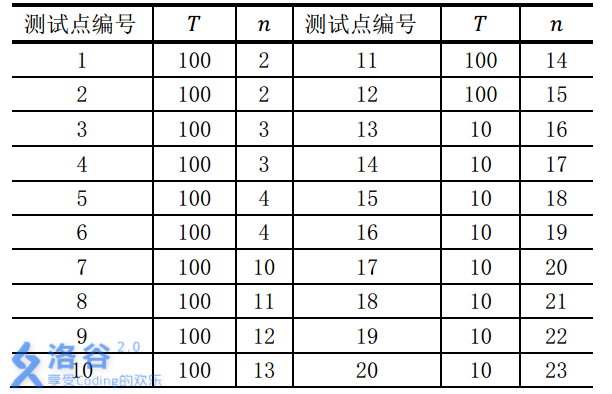
数据保证:所有的手牌都是随机生成的。
题解:又是一道巨恶心的dfs,先搜顺子再搜四带,三带(贪心),还要注意剪枝;
每次写这种题都煞费心血,这次在三带和四带时忘回带了;

#include<bits/stdc++.h> using namespace std; const int M = 200005; int a[M], ans; #define For(a, b, c) for(int a=b;a<=c;a++) bool check(){ For(i, 0, 14)if(a[i])return false; return true; } void init(){ memset(a, 0, sizeof(a)); ans = 0; } void dfs(int dep){ if(dep > ans)return ; if(check()){ ans = min(ans, dep); return; } int sum = 0; For(i, 0, 14) if(a[i])sum++; ans = min(ans, sum+dep); //cout<<dep<<endl; For(opt, 1, 3){ if(opt == 1){//单顺子 For(i, 3, 10){ if(a[i]){ if(a[i+1]&&a[i+2]&&a[i+3]) For(j, i+4, 14) if(!a[j])break; else { For(k, i, j)a[k]--; dfs(dep+1); For(k, i, j)a[k]++; } } } For(i, 3, 12){ if(a[i]>=2){//双顺子 if(a[i+1]>=2) For(j, i+2, 14) if(a[j]<2)break; else { For(k, i, j)a[k]-=2; dfs(dep+1); For(k, i, j)a[k]+=2; } } } For(i, 3, 13){//三顺子 if(a[i]>=3) For(j, i+1, 14) if(a[j]<3)break; else { For(k, i, j)a[k]-=3; dfs(dep+1); For(k, i, j)a[k]+=3; } } } if(opt == 2){ For(i, 2, 14) if(a[i] == 4){//四带 a[i]-=4; For(j, 0, 14){ if(a[j]){ a[j]--; For(k, j, 14) if(a[k]){ a[k]--; dfs(dep+1); a[k]++; } a[j]++; } } For(j, 0, 14){ if(a[j]>=2){ a[j]-=2; For(k, j, 14) if(a[k]>=2){ a[k]-=2; dfs(dep+1); a[k]+=2; } a[j]+=2; } } a[i]+=4;//! } } if(opt == 3){ For(i, 2, 14) if(a[i]>=3){//三带 a[i]-=3; dfs(dep+1); For(j, 0, 14) if(a[j]){ a[j]--; dfs(dep+1); a[j]++; } For(j, 0, 14) if(a[j]>=2){ a[j]-=2; dfs(dep+1); a[j]+=2; } a[i]+=3;//! } } } } int main(){ //freopen("landlords.in","r",stdin); //freopen("landlords.out","w",stdout); int T, n; scanf("%d%d",&T,&n); while(T--){ init(); For(i, 1, n){ int u, v; scanf("%d%d",&u,&v); if(u == 1)u = 14; a[u]++; } For(i, 0, 14) if(a[i])ans++; dfs(0); printf("%d ",ans); } }
