前言
二项分布与超几何分布是两个非常重要的、应用广泛的概率模型,实际中的许多问题都可以利用这两个概率模型来解决.在实际应用中,理解并区分两个概率模型是至关重要的.下面举例进行对比辨析.
一、概念辨析
- 超几何分布
一般的,在含有(M)件次品的(N)件产品中,任取(n)件,其中恰有(X)件次品,则事件({X=k})发生的概率为(P(X=k)=cfrac{C_M^kcdot C_{N-M}^{n-k}}{C_N^n}),((k=0,1,2,cdots,m)),其中(m=min{M,n}),且(nleq N),(Mleq N),(n),(M),(Nin N^*),称这样的分布列为超几何分布列,如果随机变量(X)的分布列具有下表的形式,则称随机变量(X)服从超几何分布。
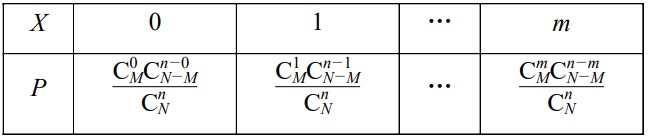
如果(X)服从参数为(n),(M),(N)的超几何分布,记作(Xsim H(n,M,N)),其数学期望(E(X)=cfrac{nM}{N})。
- 二项分布
一般的,在(n)次独立重复试验中,设事件(A)发生的次数为(X),每次试验中事件(A)发生的概率为(p),则事件(A)恰好发生(k)次的概率为(P(X=k)=C_n^kcdot p^kcdot (1-p)^{n-k}),((k=0,1,2,cdots,n)),此时称随机变量(X)服从二项分布,记为(Xsim B(n,p)),并称(p)为成功概率,称(1-p)为失败概率,当然成功和失败只是抽象的说法。
解释:二项展开式([p+(1-p)]^n=1^n=1)中,事件(A)发生(k)次,即对应展开式中的含(p^k)的项,其为(C_n^kcdot p^kcdot C_{n-k}^{n-k}cdot (1-p)^{n-k}),即(P(X=k)=C_n^kcdot p^kcdot (1-p)^{n-k}),
若随机变量(X)服从二项分布,记为(Xsim B(n,p)),则(E(X)=np),(D(X)=np(1-p));
二、案例剖析
袋中有8个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求:
(1)有放回抽样时,取到黑球的个数(X)的分布列;
(2)不放回抽样时,取到黑球的个数(Y)的分布列.
解:(1)有放回抽样时,取到的黑球数(X)可能的取值为0,1,2,3.
又由于每次取到黑球的概率均为(cfrac{2}{10}=cfrac{1}{5}),3次取球可以看成3次独立重复试验,
故随机变量服从二项分布(Xsim Bleft(3,cfrac{1}{5} ight)),则有
(P(X=0)=C_3^0(cfrac{1}{5})^0(cfrac{4}{5})^3=cfrac{64}{125});
(P(X=1)=C_3^1(cfrac{1}{5})^1(cfrac{4}{5})^2=cfrac{48}{125});
(P(X=2)=C_3^2(cfrac{1}{5})^2(cfrac{4}{5})^1=cfrac{12}{125});
(P(X=3)=C_3^3(cfrac{1}{5})^3(cfrac{4}{5})^0=cfrac{1}{125})
则随机变量(X)的分布列如图所示。
<img src="https://images2018.cnblogs.com/blog/992978/201804/992978-20180403162251168-1958930523.png" width=25% height=25% / >
(2)不放回抽样时,取到的黑球数(Y)可能的取值为0,1,2.
且有(Ysim Hleft(10,3,2 ight)) (hspace{2cm}) (Ysim Hleft(N,n,M ight))
(P(Y=0)=cfrac{C_2^0C_8^3}{C_{10}^3}=cfrac{7}{15});
(P(Y=1)=cfrac{C_2^1C_8^2}{C_{10}^3}=cfrac{7}{15});
(P(Y=2)=cfrac{C_2^2C_8^1}{C_{10}^3}=cfrac{1}{15});
则随机变量(Y)的分布列如图所示。
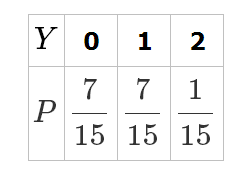
【感悟反思】:1、注意这两个概率模型的区别和联系,二项分布的典型例子就是一个熟练射手的(n)次射击;超几何分布的典型例子就是抽次品。
2、通过此例可以看出:有放回抽样时,每次抽取时的总体没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复试验,此种抽样是二项分布模型.而不放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模型.因此,二项分布模型和超几何分布模型最主要的区别在于是有放回抽样还是不放回抽样.所以,在解有关二项分布和超几何分布问题时,仔细阅读、辨析题目条件是非常重要的.
三、如何区分
- 超几何分布的特征:
①考查对象分两类,当然在具体题目中可能需要我们将数据人为分为两类。
②已知各类对象的个数;
③从中抽取若干个个体,考查某类个体的个数(X)的概率分布;
④主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型。
- 二项分布的特征:
①每次试验中,事件发生的概率是相同的;
②各次试验中的事件是相互独立的;
③每次试验只有两种结果:事件要么发生,要么不发生;
④随机变量是这(n)次独立重复试验中事件发生的次数。
②超几何分布是不放回抽取,而二项分布是有放回抽取(独立重复);
③由解题的实际经验可得,题目中给定了概率的,基于概率计算的往往是二项分布;题目中给定了数字,基于数字计算概率的往往是超几何分布。
四、实例总结
- 超几何分布的常见实例
①10件产品中含有3件次品,从中任意取4件产品,所取出的次品件数服从超几何分布;
②袋中有8红球4白球,从中任意摸出5个球,摸出红球个数服从超几何分布;
③某班45个学生,女生20人,现从中选7人做代表,代表中所含女生的人数服从超几何分布;
④15张卡片中含有5件写有“奖”字,从中任意取3件产品,所取出的卡片中含有奖字的卡片张数服从超几何分布;
⑤10位代表中有5位支持候选人(A),随机采访3人,其中支持候选人(A)的人数服从超几何分布;
⑥盘中装有10个粽子,豆沙粽2个,肉粽3个,白粽5个,从中任选3个,取到的豆沙粽的个数服从超几何分布;
注意:在具体题目中,可能需要将上述的三类数据转化为两类数据:豆沙粽子和非豆沙粽子。
- 二项分布的常见实例
①一个狙击手连续射击10次,每次中10环的概率都是0.98,则其击中10环的次数服从二项分布;
②10个狙击手各射击1次,每人击中10环的概率都是0.95,则其击中10环的人数服从二项分布;
③抛掷(n)枚相同的骰子,(X)为出现点数为1的骰子数;则(Xsim B(n,cfrac{1}{6}));
④(n)个新生婴儿,(X)为男婴的个数,则(Xsim B(n,cfrac{1}{2}));
⑤某产品的次品率为(p),(X)为(n)个产品中的次品数,(Xsim B(n,p));
⑥女性患色盲的概率为(0.25\%),(X)为任取(n)个女人中患色盲的人数,(Xsim B(n,0.25\%));
⑦吊灯上并联着5个灯泡,每个正常工作的概率都是0.7,则正常工作的灯泡数(Xsim B(5,0.7));
⑧用户购买100件某产品,该产品的质量指标值位于((187.7,212.2))之间的概率都是(0.6826),(X)表示质量指标值位于((187.7,212.2))之间的产品件数,则(Xsim (100,0.6826));
⑨从该市学生中随机选取5名学生,记(xi)为身高在((1.50,1.70))的学生人数,且身高在((1.50,1.70))的频率为(0.7),则(xisim (5,0.7));
五、典例剖析
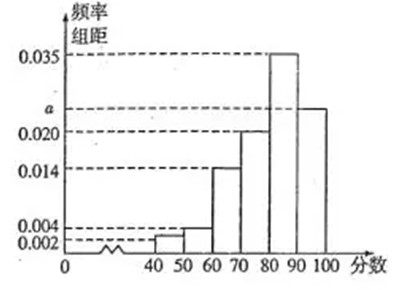
2018年春节期间,为了解市民对西安地铁运营状况的满意度,分别从不同地铁站点随机抽取若干市民对其评分(满分为100分,评分均为整数),绘制频率分布直方图,并将分数从低到高分为四个等级:

(1)若市民的满意度评分相互独立,以满意度样本估计全市市民满意度。现从全市市民中随机抽取了4人,估计这4人中至少有2人非常满意的概率;
(2)在等级为不满意市民中,老年人占比(cfrac{1}{3}),现从该等级市民中按年龄分层抽取了15人了解不满意的原因,并从中选取3人担任整改督导员,记(X)为老年督导员的人数,求(X)的分布列和数学期望(E(X)).
(3)相关部门对西安地铁运营状况进行评估,评估的硬指标是:市民对西安地铁运营状况的满意指数不低于0.8,否则需要整改,根据你所学的统计知识,判断地铁运营状况能否通过评估,并说明理由。
(备注:满意指数=(cfrac{满意程度的平均分}{100}))
【分析】:(1)首先由频率分布直方图计算得到(a=0.025),市民非常满意的概率为(0.025 imes 10=0.25=cfrac{1}{4}),
注解:由题目可知市民的满意度评分相互独立,随机抽取4人做调查,到此我们就可以理解相当于做了4次独立重复试验,每次试验满意概率为(cfrac{1}{4}),不满意概率为(cfrac{3}{4}),这样就只能考虑二项分布而不是超几何分布了。
令满意人数为(X),则(Xsim B(4,cfrac{1}{4})),且(P(X=k)=C_4^kcdot (cfrac{1}{4})^kcdot (cfrac{3}{4})^{4-k}),(k=0,1,2,3,4)
故所求的概率即(P=P(X=2)+P(X=3)+P(X=4)=cfrac{67}{256}),
或(P=1-P(X=0)-P(X=1)=1-C_4^0cdot (cfrac{1}{4})^0cdot (cfrac{3}{4})^{4}-C_4^1cdot (cfrac{1}{4})^1cdot (cfrac{3}{4})^{3}=cfrac{67}{256}).
(2)抽取的15中,老年人占(15 imes cfrac{1}{3}=5),其他人占10人,从中抽取3人担任督导员,是无放回抽取,故容易理解是超几何分布。
且 (Xsim Hleft(15,5,3 ight)),(P(X=k)=cfrac{C_5^kC_{10}^{3-k}}{C_{15}^3},k=0,1,2,3);
故(P(X=0)=cfrac{C_5^0C_{10}^{3}}{C_{15}^3}=cfrac{24}{91}),(P(X=1)=cfrac{C_5^1C_{10}^{2}}{C_{15}^3}=cfrac{45}{91}),
(P(X=2)=cfrac{C_5^2C_{10}^{1}}{C_{15}^3}=cfrac{20}{91}),(P(X=3)=cfrac{C_5^3C_{10}^{0}}{C_{15}^3}=cfrac{2}{91}),
分布列从略。
(EX=0 imes cfrac{24}{91}+1 imescfrac{45}{91}+2 imescfrac{20}{91}+3 imescfrac{2}{91}=1)
(3)由频率分布直方图求平均数,得到,
((45 imes 0.002+55 imes 0.004+65 imes 0.014+75 imes 0.02+85 imes 0.035+95 imes 0.025) imes 10=80.7)
即市民满意度的平均分为(80.7),满意度指数为(cfrac{80.7}{100}=0.807>0.8);
即地铁运营状况能够通过验收。
高一某班有(6)男(4)女参加心理社,在这(10)名同学中,有(4)名同学初中毕业于同一个学校,其余(6)名同学都毕业于其他(6)所不同的学校,现从这(10)名同学中随机抽取(4)名同学参加某活动(每位同学被选到的概率都相同)。
(1)求选出的(4)名同学初中毕业于不同学校的概率;
分析:从(10)名同学中任取(4)名同学,共有(C_{10}^4)种等可能的结果,故属于古典概型,
令“选出的4人初中毕业于不同学校”为事件(A),
【法1】直接法,从正面求解,选出的4人的毕业学校全不相同,
则(P(A)=cfrac{C_{4}^0 cdot C_{6}^4+C_{4}^1 cdot C_{6}^3 }{C_{10}^4}=cfrac{80+15}{210}=cfrac{19}{42})
【法2】间接法,从反面求解,选出的4人的毕业学校不全相同,
则(P(A)=1-cfrac{C_{4}^4 cdot C_{6}^0+C_{4}^3 cdot C_{6}^1+C_{4}^2 cdot C_{6}^2 }{C_{10}^4}=cfrac{19}{42})
(2)设(X)为选出的(4)名同学中的女同学,求随机变量(X)的分布列和数学期望;
分析:随机变量(X)的所有可能取值为(0,1,2,3,4),则其服从超结合分布,
(P(X=k)=cfrac{C_{4}^k cdot C_{6}^{4-k}}{C_{10}^4}),((k=0,1,2,3,4))
则有(P(X=0)=cfrac{C_{4}^0 cdot C_{6}^4}{C_{10}^4}=cfrac{15}{210}=cfrac{1}{14});
(P(X=1)=cfrac{C_{4}^1 cdot C_{6}^3}{C_{10}^4}=cfrac{4 imes 20}{210}=cfrac{8}{21});
(P(X=2)=cfrac{C_{4}^2 cdot C_{6}^2}{C_{10}^4}=cfrac{6 imes 15}{210}=cfrac{3}{7});
(P(X=3)=cfrac{C_{4}^3 cdot C_{6}^1}{C_{10}^4}=cfrac{24}{210}=cfrac{4}{35});
(P(X=4)=cfrac{C_{4}^4 cdot C_{6}^0}{C_{10}^4}=cfrac{1}{210});
故分布列如下,现略;
期望(EX=0 imes cfrac{1}{14}+1 imes cfrac{8}{21}+2 imes cfrac{3}{7}+3 imes cfrac{4}{35}+4 imes cfrac{1}{210}=cfrac{8}{5})。