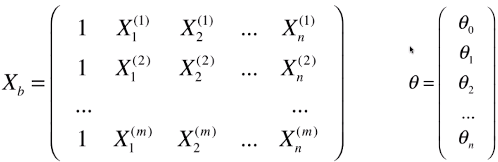一、梯度下降法基础
- 定义:梯度下降法不是一个机器学习算法,是一种基于搜索的最优化方法;
- 功能:最优化一个损失函数;
- 梯度上升法:最大化一个效用函数;
- 机器学习中,熟练的使用梯度法(下降法、上升法)求取目标函数的最优解,非常重要;
- 线性回归算法模型的本质就是最小化一个损失函数,求出损失函数的参数的数学解;
- 很多机器学习的模型是无法求出目标函数的参数的最优解;
- 梯度下降法是在机器学习领域中最小化损失函数的最为常用的方法;
1)梯度下降法的逻辑思路
- 每次改变一点参数theta,目标函数 J 跟着改变,不断的递进改变参数值,得到目标函数的极值;经过多次运行,每次随机选取初始化的点,得出不同的局部最优解(极值),比较所有最优解,最小/最大的合格值就是目标函数的最值;
- theta:模型中的参数,而不是模型中的变量;(以线性回归模型为例)
- 模型中的每一个 X 表示一个样本,每一个 y 表示该样本对应的值;
- y = X.dot(θ):结果为一个数值;
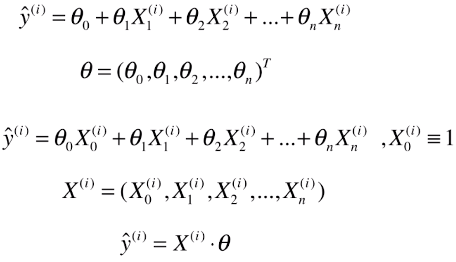
- 变量 theta 的变化量 = 学习率 X 梯度/导数
- new_theta = last_theta - theta的变化量
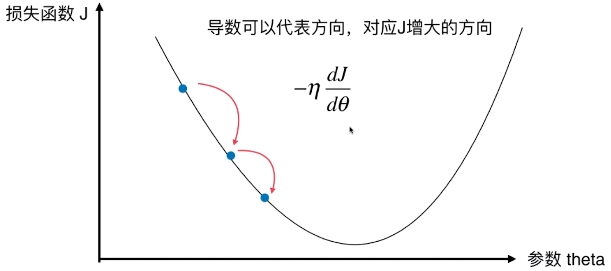
- 损失函数 J 应该有一个最小值,对于最小化一个损失函数来说,相当于在此坐标系中,寻找一个点参数theta使得 J 取得最小值
- 导数可以代表函数变化的方向,对应 J 增大的方向,因为公式前加了符号 “ - ” ;
- η:学习率(Learning rate)
- η 的取值影响获得最优解的速度;
- η 取值不合适,甚至得不到最优解;
- η 是梯度下降法的一个超参数;一般需要调参找到最适合的 η;
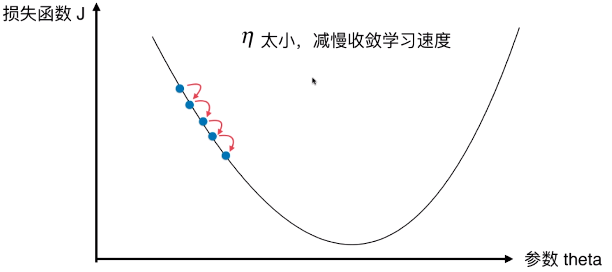
- η 太小,减慢收敛学习速度
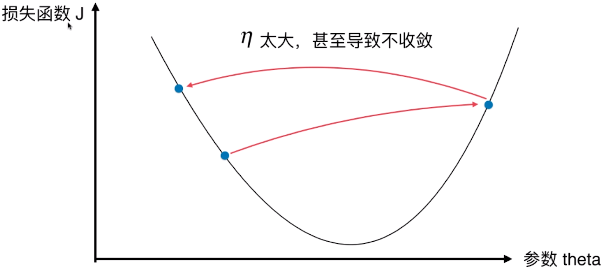
- η 太大,导致不收敛
- 如果出现 J 的变化有减有曾,可能是 η 的取值太大;
- 收敛:得到极值的过程
2)梯度下降法的问题
- 问题:并不是所有的函数都有唯一的极值点,优化的目标是找到最小值点;
- 方案:多次运行,随机化初始点,比较后取最优解;
- 方案弊端:也不一定能找到全局最优解;
3)其它
- 直线方程中导数代表斜率;
- 曲线方程中导数代表在这一点的切线的斜率;
- 为什么叫梯度:在多维函数中,要对各个方向的分量分别求导,最终得到的方向就是梯度;
- 多维函数中,梯度代表函数变化的方向,对应 就 J 增大/减小的方向;
- 梯度下降法的初始点也是一个超参数,起始点对于一个算法是非常重要的;
二、程序模拟梯度下降法原理
1)具体实现
# 模拟损失函数:y = (x - 2.5)**2 - 1
# 数据集特征值:plot_x = np.linspace(-1, 6, 141)
- 代码
import numpy as np import matplotlib.pyplot as plt # np.linspace(-1, 6, 141):将区间[-1, 6]等分成141份,包含-1和6 plot_x = np.linspace(-1, 6, 141) # 记录搜索过程中的theta值 theta_history = [] # 1)计算当前theta值对应的损失函数的导数值 def dJ(theta): return 2*(theta-2.5) # 2)计算当前theta值对应的损失函数值 # 在计算损失函数时添加异常检测功能 # 设置异常检测原因:当 eta 过大时,使得损失函数是不断增大的,也就得不到满足精度的损失函数值,就会报错 # 异常检测:没有异常时执行try,有异常时执行except # 此处执行except时返回浮点数的最大值 def J(theta): try: return (theta-2.5)**2 - 1. except: return float('inf') # 3) 梯度下降,循环搜索,获取局部最优解 # 一般判断函数的极值点位置:导数 == 0 # 如何判断theta是否来到的极值点? # 问题:编程具体实现的时候,有可能由于eta设置的不合适,或者求导时有浮点精度,使得求取的损失函数最小值所对应的theta点,不是导数刚好等于 0 的点 # 循环结束:当前的损失函数值 - 上一次的损失函数值之间的差 < 精度,此时停止循环,以为当前的损失函数值为局部最优解 # initial_theta:theta的初始值 # eta:学习率 # n_iters:循环次数,默认10000次;(如果不设定循环次数,程序出现死循环时会一直执行) # espsilon:精度,默认10**-8 def gradient_descent(initial_theta, eta, n_iters = 10**4, espsilon=10**-8): theta = initial_theta theta_history.append(initial_theta) i_iter = 0 while i_iter < n_iters: # 循环开始时,先求取当前theta所对应的梯度 gradient = dJ(theta) # abs(x):求x的绝对值 last_theta = theta theta = theta - eta * gradient theta_history.append(theta) if(abs(J(theta) - J(last_theta)) < epsilon): break # 每进行一次循环,得不到结果时,记录一次循环次数 # 如果得到了结果,break直接终端循环 i_iter += 1 # 4)绘制参数与损失函数的关系图形、绘制循环搜索过程中的theta值与损失函数的关系图 def plot_theta_history(): plt.plot(plot_x, J(plot_x)) plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r', marker='+') plt.show()
- 其它
- 计算当前theta值对应的损失函数 J 的值时,要进行异常检测;
原因:当 eta 过大时,使得损失函数是不断增大的,也就得不到满足精度的损失函数值,就会报错;
- 如何判断theta是否来到了极值点?
方案:设定精度,当前的损失函数值 - 上一次的损失函数值之间的差 < 精度,此时停止循环,以为当前的损失函数值为局部最优解; - 问题:
①、一般判断函数的极值点位置:导数 == 0
②、编程具体实现的时候,有可能由于eta设置的不合适,或者求导时有浮点精度,使得求取的损失函数最小值所对应的theta点,不是导数刚好等于 0 的点;
- 梯度下降,循环搜索时,设定循环次数;
原因:如果不设定循环次数,程序出现死循环时会一直执行;
- np.linspace(-1, 6, 141):将区间 [-1, 6] 等分成141个点,包含 -1 和 6;
- abs(x):返回x的绝对值;
2)给定不同的学习率、初始值,查看优化情况
-
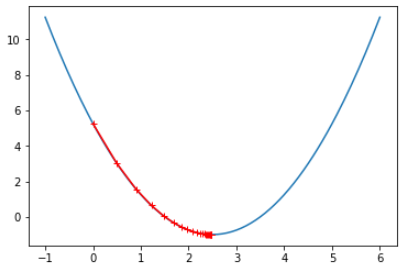
eta = 0.1 theta_history = [] gradient_descent(0., eta) plot_theta_history() # len(theta_history) == 46
-
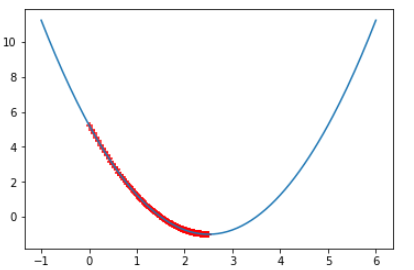
eta = 0.01 theta_history = [] gradient_descent(0., eta) plot_theta_history() # len(theta_history) == 424
-
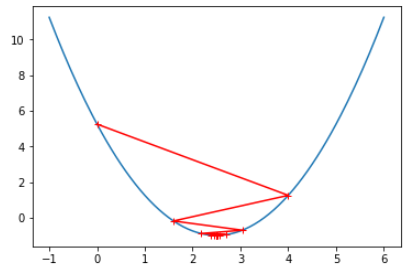
eta = 0.8 theta_history = [] gradient_descent(0., eta) plot_theta_history() # len(theta_history) == 22
-
eta = 1.1 theta_history = [] gradient_descent(0., eta, n_iters=10) plot_theta_history() # len(theta_history) == 10001
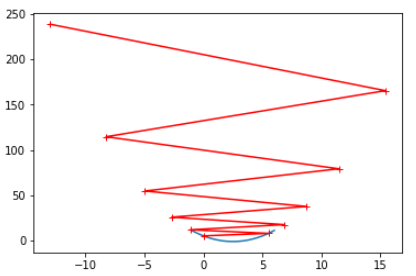
- 分析
-
现象:搜索开始时 J 和 theta 变化都比较大,最后变化较小;(搜索点的分布:由疏到密)
# 原因:theta的每次变化量 == eta * 2 * (theta-2.5),随着theta的不断减小,每次的变化量也会减小,因此水平方向上点的分布越来越密
另外,由J == (theta - 2.5) ** 2 - 1看出,每次的 J 的变化量也会减小,因此垂直方向上点的分布也会越来越密
# 变化量 == 学习率 X 导数,导数 == 2*(theta - 2.5),new_theta == last_theta — last_变化量