Special Prime
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 676 Accepted Submission(s):
358
Problem Description
Give you a prime number p, if you could find some natural number (0 is not inclusive) n and m, satisfy the following expression:
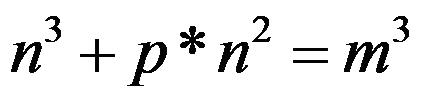
We call this p a “Special Prime”.
AekdyCoin want you to tell him the number of the “Special
Prime” that no larger than L.
For example:
If L =20
13 + 7*12 =
23
83 + 19*82 = 123
That is to say the prime number 7, 19 are two
“Special Primes”.
Input
The input consists of several test cases.
Every case has only one integer indicating L.(1<=L<=106)
Every case has only one integer indicating L.(1<=L<=106)
Output
For each case, you should output a single line indicate
the number of “Special Prime” that no larger than L. If you can’t find such
“Special Prime”, just output “No Special Prime!”
Sample Input
7 777
Sample Output
1 10

题意
求1—L范围内,满足 n3+p*n2=m3 的质数p的数量(m,n > 0) 。
题解
0~30 O( P2 ) 暴力枚举 n,m 判断 p 是否合法,在 n,m 枚举结束时,取一个较大值 P。
100 O[ (√L)2 ](实际可能更优)
由原式化简可得 n2 * (n+p) = m3 ,
若 n2 和 n+p 间有公共素因子 p ,
那么 n+p = k * p ,
即 n = p * (k-1) ,
带回原式得到 p3 * (k-1)2 * k = m3 ,
易证 (k-1)2 * k 不能用某一个正整数的三次幂表示,所以此情况不成立。
由此可以假设 n = a3 ,n+p = b3 ,
相减得到 p = b3 - a3 ,
根据立方差公式有 p = (b-a) * (a2 + a*b + b2) ,
由于 p 是素数,(a2 + a*b + b2) != 1 ,所以 b-a = 1,
带入 b 化简可得 p = 3 * a * a + 3 * a + 1 ,
暴力枚举 a ,算出 p ,判断 p 是否是素数,统计一下就得到答案了。
代码
1 #include<cstdio> 2 using namespace std; 3 int L,ans; 4 bool Prime(int x){ 5 for(int i=2;i*i<=x;i++) 6 if(x%i==0) return 0; 7 return 1; 8 } 9 int main(){ 10 while(~scanf("%d",&L)){ 11 ans=0; 12 for(int i=1;3*i*i+3*i+1<=L;i++){ 13 if(Prime(3*i*i+3*i+1)) ans++; 14 } 15 if(ans==0) printf("No Special Prime! "); 16 else printf("%d ",ans); 17 } 18 return 0; 19 }