排序算法小汇总
1、交换排序类
1.1、冒泡排序
1.2、快速排序
2、选择排序类
2.1、简单选择排序
2.2、堆排序
3、插入排序类
3.1、直接插入排序
3.2、希尔排序
4、归并排序
5、基数排序
交换排序类
冒泡排序(优化)
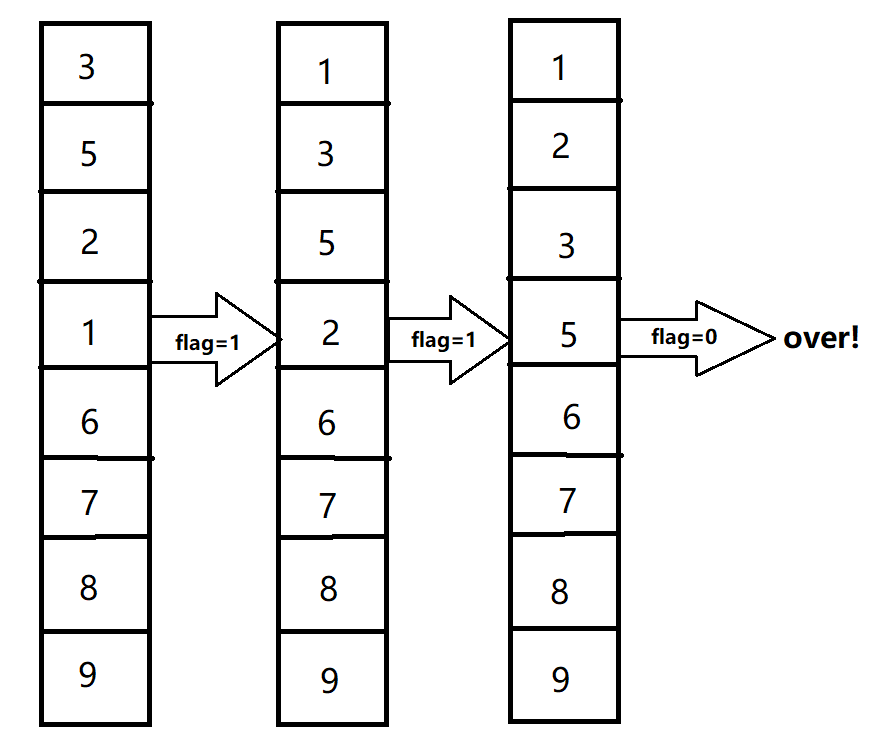
冒泡排序一般将前面作为有序区(初始无元素),后面作为无序区(初始元素都在无序区里),在遍历过程中把当前无序区最小的数像泡泡一样,让其往上飘,然后在无序区继续执行此操作,直到无序区不再有元素。
这块是对老式冒泡排序的一种优化,因为当某次冒泡结束后,可能数组已经变得有序,继续进行冒泡排序会增加很多无用的比较次数,提高时间复杂度。
所以我们增加了一个标识变量flag,将其初始化为1,外层循环还是和老式的一样从0到末尾,内存循环我们改为从最后面向前面i(外层循环所处的位置)处遍历找最小的,如果在内存没有出现交换,说明无序区的元素已经变得有序,所以不需要交换,即整个数组已经变得有序。
#include<iostream>
using namespace std;
void sort(int k[] ,int n)
{
int flag = 1;
int temp;
for(int i = 0; i < n-1 && flag; i++)
{
printf("hello
");
for(int j = n-1; j > i; j--)
{
flag = 0;
/*下面这里和i没关系,注意看这块,从下往上travel,两两比较,如果不合适就调换,
如果上来后一次都没调换,说明下面已经按顺序拍好了,上面也是按顺序排好的,所以完美!
*/
if(k[j-1] > k[j])
{
temp = k[j-1];
k[j-1] = k[j];
k[j] = temp;
flag = 1;
}
}
}
}
int main()
{
int k[3] = {0,9,6};
sort(k,3);
for(int i =0; i < 3; i++)
printf("%d ",k[i]);
}
快速排序
快速排序(Quicksort),基于分治算法思想,是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
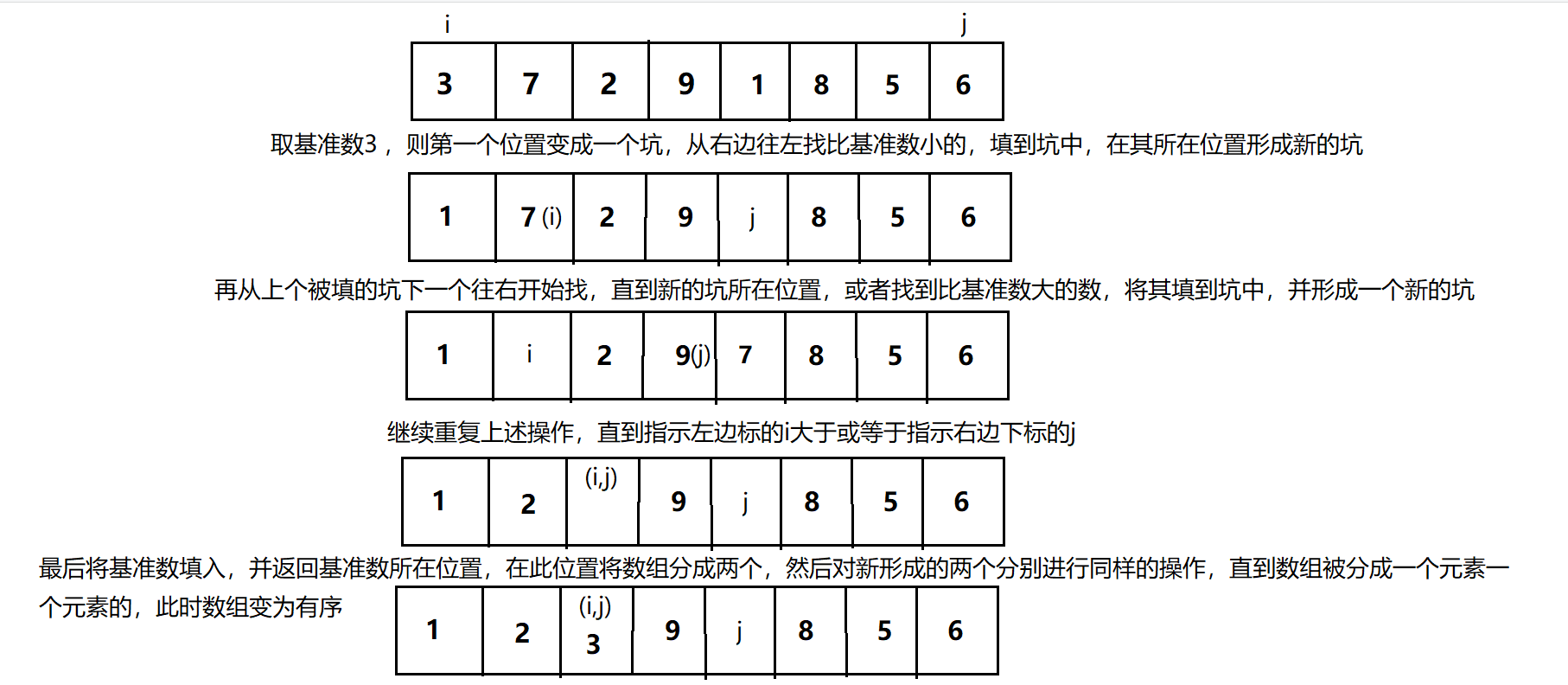
通俗来说,就是不断的挖坑和填坑
- 1、其实就是先选择一个基准数,然后这个基准数我们保存为x,那它所在的位置就是一个空出来的坑。
- 2、我们从右向左迭代,如果遇到比基准数小的数,就将其填到上次挖的坑中,然后它自己在的这个地方就变成了一个新的坑。
- 3、然后再从左向右迭代,找比基准数大的数,将其填到上次挖的坑中,然后它所在的地方就变成了新的坑。
- 4、最后要将基准数填入最后的坑中,然后将基准数所在的位置返回,方便下次调用时候使用
//挖坑填数
int adjustArray(int s[],int l, int r) //传入数组和左右的下标
{
int i = l,j = r; //分别表示左半边的下标和右半边的下标
int x = s[l]; //默认最左边的数就是挖的第一个坑
while(i < j) //要保证数组中元素最少有两个
{
//从右向左迭代,找比基准数小的
while(s[j] >= x && i < j)
j--;
if(i < j) //找到了比基准数小的
{
s[i] = s[j]; //将其填到原来挖的坑的地方上,现在j处又形成了一个新的坑
i++; //i处填入了新的数,所以i++,然后从左往右去找,在左半边比基准数大的数
}
//从左向右迭代去找比基准数大的
while(s[i] < x && i < j)
i++;
if(i < j)
{
s[j] = s[i];
j--;
}
}
//退出时,要把坑用基准数填回去
s[i] = x;
return i; //返回调整后基准数的位置,方便下一次递归调用的时候
}
就这样将原来的数组以返回的基准数所在的位置为中心,分成了两个数组(理论上两个,但在内存中还是在一起挨着的),然后分别对新的两个数组递归进行挖坑和填坑的操作,当先前指示数组左右两边的下标的变量左边的大于或等于(一般都是等于)右边的时候(即数组已经被分的不能被分了),这时候原数组就变成有序的了,因为按照上面的思路,所有左边的都小于右边的,那既然数组都被分的变成一个数一个小数组那就是左边的数比右边的数小,即有序,排序完成!
void quick_sort(int s[], int l, int r)
{
if(l < r)
{
int i = adjustArray(s,l,r);
//不能将上次的基准数拉入新的两个数组中的任何一个,因为其所在的位置已经是最终对的位置了,它左边的数都比它小,右边的都比它大
quick_sort(s,l,i-1);
quick_sort(s,i+1,r);
}
}
选择排序类
简单选择排序
选择排序就是每次在无序区循环找出一个极值,将其放入指定位置(即进入有序区)来使数组有序,一般来说是让数组的左边作为有序区,右边是无序区。
- 先从第一个元素到最后一个元素遍历,找出最小的元素,将其和第一个元素互换位置。
- 再从第二个元素到最后一个元素遍历,找出最小的,和第二个互换位置。
- 如此循环,右边无序区只剩一个元素,则排序完成!
#include<iostream>
using namespace std;
void sort(int k[],int n)
{
int min,temp; //min用来保存最小的元素的下标
for(int i = 0;i < n-1; i++)
{
min = i;
for(int j = i+1; j < n; j++) //找出无序区中的最小的元素
{
if(k[j] < k[min])
min = j;
}
if(min != i) //如果最小的元素,不是初始的,即有比它更小的就交换位置
{
temp = k[min];
k[min] = k[i];
k[i] = temp;
}
}
}
int main()
{
int k[10] = {2,5,4,6,3,8,9,7,1,0};
sort(k,10);
for(int i = 0;i < 10;i++)
cout<<k[i]<<" ";
}
堆排序
堆排序采用大顶堆或着小顶堆,我们这里采用大顶堆来排序。
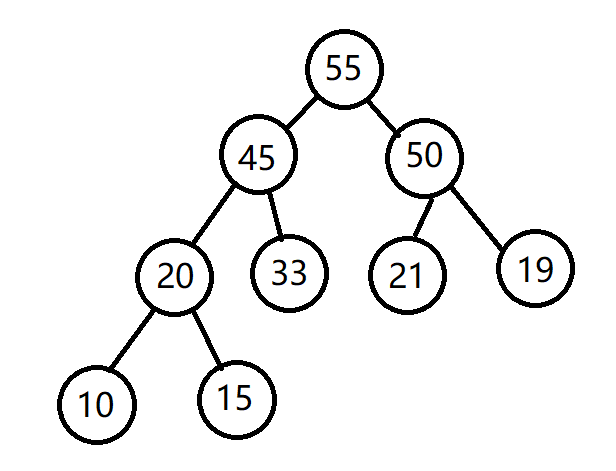
用一棵完全二叉树来模拟一个大顶堆,大顶堆的规则如下:每个结点的值都大于它的孩子结点的值,如下图:
这样,如果我们每次将大顶堆的根节点依次和数组的最后一个,倒数第二个,倒数第三个......做交换,每次交换完后,需要从根节点到与之交换的那个结点之前的结点之间进行调整大顶堆,保证大顶堆的符合上述规则。
在完全二叉树中,如果用顺序结构来存储这棵树,那么某个结点和它左右孩子结点之间存在以下关系(层序遍历):左孩子下标等于双亲结点下标的2倍,右孩子下标等于双亲结点2倍+1。
交换函数
void swap(int k[], int i, int j)
{
int temp = k[i];
k[i] = k[j];
k[j] = temp;
}
调整大顶堆的函数
void HeapAdjust(int k[], int s, int n) //从s到n开始调整大顶堆,s表示待调整的结点
{
int temp = k[s]; //保存当前需要调整的结点
for(int i = 2*s; i <= n; i*=2) //2*s表示s这个结点的左孩子,i*=2表示当前结点的左孩子结点,也就是下一个检查的结点,因为移动当前检查的结点后,可能会对其孩子结点的规则完整性破坏,所以需要往下检查
{
if(i < n && k[i] < k[i+1]) //k[i]表示左孩子,k[i+1]表示右孩子,i<n是为了保证不是最后一个结点
{
i++; //永远让i指向较大的孩子结点
}
if(temp >= k[i]) //如果待调整的双亲大于两孩子中较大的孩子,则不需要调整
{
break;
}
//下面将较大的更新为双亲结点
k[s] = k[i];
s=i;
}
k[s] = temp;
}
/**
对上面for循环做一个解释,当检查到较上的结点时候,移动后不能保证树的规则,
应该继续检查其孩子结点,因为做了交换后可能会破坏孩子结点的大顶堆规则
*/
对堆排序的实现
为了方便起见,数组不用第0号元素,从第一号元素开始。
假设一共n个结点,第n/2个结点刚好是最后一个拥有孩子结点的结点,这个也是完全二叉树的规律,而初始我们就应该从下往上去检查,因为上面的结点是根据下面的结点检查的。
#include <iostream>
using namespace std;
void HeapSort(int k[], int n)
{
for(int i = n/2; i > 0; i--)//第n/2个结点刚好是最后一个拥有孩子结点的结点,这个也是完全二叉树的规律
{
HeapAdjust(k,i,n);
}
for(int i = 1; i < 10; i++) //此处是为了调试,查看交换前第一次构造的大顶堆
cout<<k[i]<<" ";
for(int i = n; i > 1; i--)
{
swap(k,1,i);
HeapAdjust(k,1,i-1);
}
}
int main()
{
int k[10] = {-1,3,2,7,5,8,9,0,1,6};
HeapSort(k,9);
system("pause"); //此处是为了做一下调试,查看交换前构造的第一个大顶堆
for(int i = 1; i < 10; i++)
cout<<k[i]<<" ";
}
插入排序类
直接插入排序
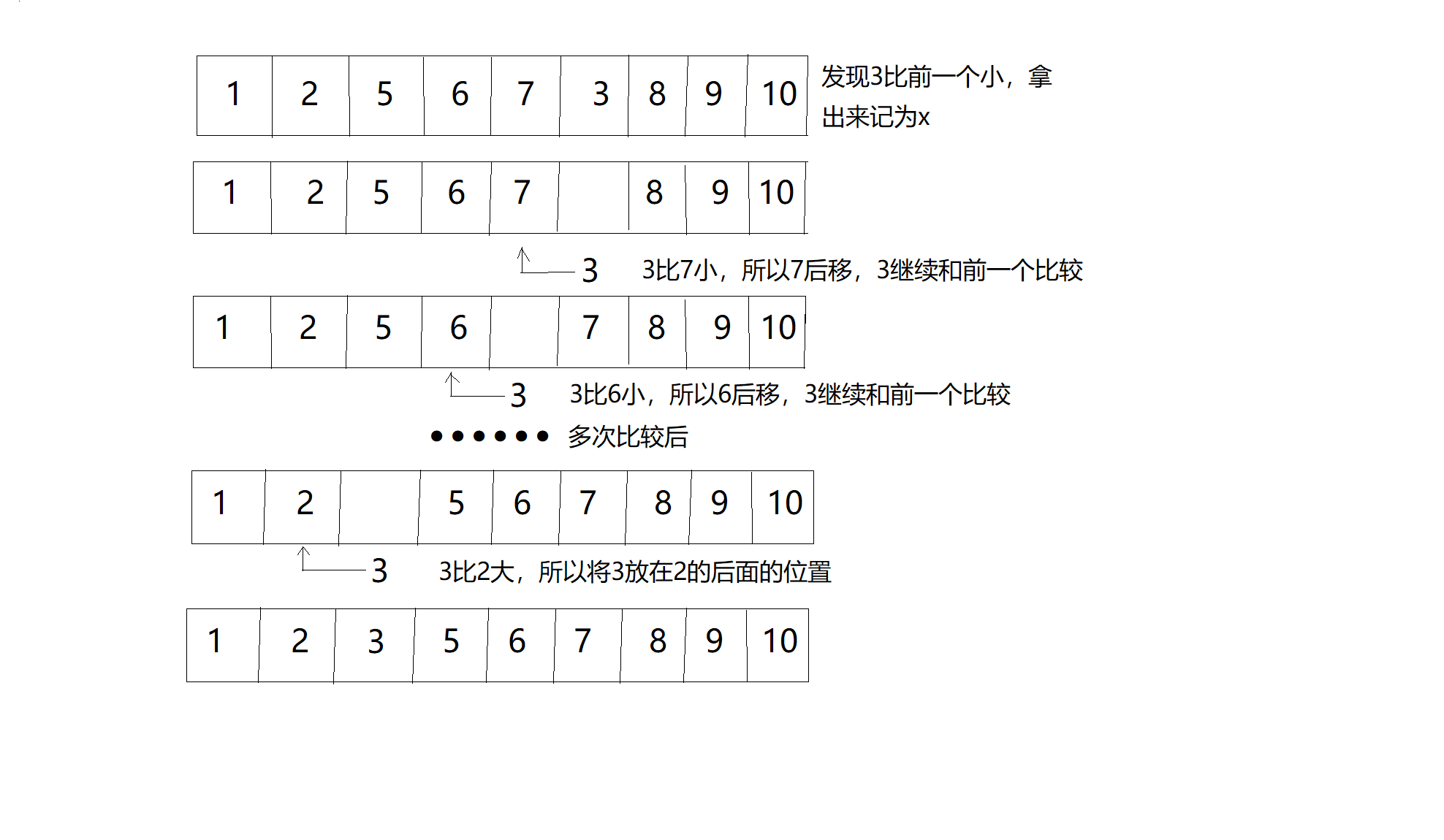
(从小到大排列)直接插入排序就是:遍历这个数组,然后如果发现后一个比前一个小,则将后一个较小的拿出来,记为x,然后与前面的依次作比较,如果比x大,则将其向后退一个位置,直到碰到一个比x小的元素,则将x放到它的后面即可,这样等到遍历完这个数组后,它就会变成有序的。
下面是一次外层循环的演示,对整个数组遍历一遍,作如下操作则可
#include<iostream>
using namespace std;
void Insert_Sort(int k[],int n)
{
int temp,j,i;
for(i = 1; i < n; i++)
{
if(k[i] < k[i-1])
{
temp = k[i];
for( j = i-1; k[j] > temp && j >= 0; j--)
k[j+1] = k[j];
k[j+1] = temp;
}
}
}
int main()
{
int k[10] = {3,5,1,7,2,0,8,9,4,6};
Insert_Sort(k,10);
for(int i = 0; i < 10; i++)
cout<<k[i]<<endl;
return 0;
}
希尔排序
希尔排序是对插入排序的一种改进,先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2 < d1重复上述的分组和排序,直至所取的增量 =1( < …< d2< d1),即所有记录放在同一组中进行直接插入排序为止。
#include<iostream>
using namespace std;
void Insert_Sort(int k[],int n)
{
int temp,j,i;
int gap = n;
do
{
gap = gap/3 + 1;
for(i = gap; i < n; i++)
{
if(k[i] < k[i-gap])
{
temp = k[i];
for( j = i-gap; k[j] > temp && j >= 0; j-=gap)
{
k[j+gap] = k[j];
}
k[j+gap] = temp;
}
}
}while(gap > 1);
}
int main()
{
int k[10] = {3,5,1,7,2,0,8,9,4,6};
Insert_Sort(k,10);
for(int i = 0; i < 10; i++)
cout<<k[i]<<" ";
return 0;
}
归并排序
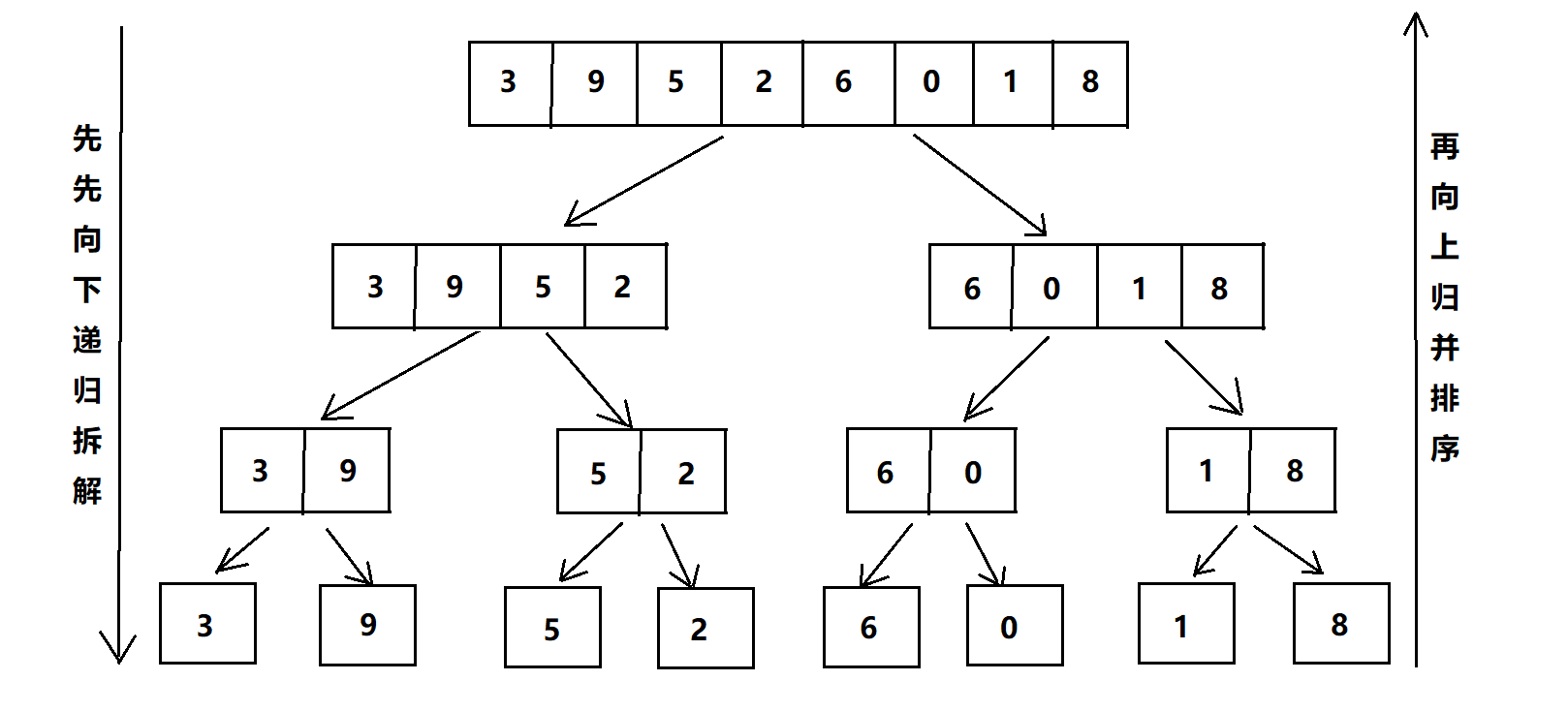
归并排序,基于分治算法思想,就比如是比武大赛一样,先对数据进行分组,两两进行比较,并排序,然后将有序的两个小数组进行归并,得到一个新数组,再和其他新得到的数组进行两两归并,如此重复,直到归并为一个大数组,此时,此数组有序!
#include <iostream>
using namespace std;
void Merge(int array[], int start, int mid, int end)
{
//start到mid表示第一个数组,mid+1到end表示第二个数组
int newarray[end - start + 1];
//对两个数组进行归并
int p = start, q = mid + 1, r = 0; //分别指示第一个数组,第二个数组,和第三个新数组
while(p <= mid && q <= end)
{
if(array[p] <= array[q])
{
newarray[r++] = array[p++];
}
else
{
newarray[r++] = array[q++];
}
}
//左侧小集合还有剩余,依次归并到大集合尾部
while(p <= mid)
{
newarray[r++] = array[p++];
}
//右侧小集合还有剩余,依次归并到大集合尾部
while(q <= end)
{
newarray[r++] = array[q++];
}
//将大集合元素依次复制回原数组
for(int i = 0; i < end - start + 1; i++) //to do
array[i+start] = newarray[i];
}
void Merge_Sort(int array[], int start, int end)
{
int mid = (start + end) / 2;
if(start < end)
{
Merge_Sort(array,start,mid);
Merge_Sort(array,mid+1,end);
//合并
Merge(array,start,mid,end);
}
}
int main()
{
int k[10] = {3,9,6,1,8,4,0,7,2,5};
Merge_Sort(k,0,9);
for (int i = 0; i < 10; ++i)
{
cout<<k[i]<<" ";
}
}
基数排序
个人理解(最好先了解一下桶排序):
从待排序数组每个数字的基数开始排序,然后一直到最大数的最高位。准备10个桶,从低位开始分别将其放入对应编号为0-9的桶中。等到低位排完得到一个子序列,再将这个序列按照次低位的大小进入相应的桶中,一直排到最高位为止,数组排序完成。
算法步骤
- 先找出所有数中的最高位数,即循环次数,要存入桶和出桶这么多次
- 每次循环用一个count[10]数组记录每个桶中的数字个数(循环开始之前,要记得将上次循环时count中保存的值初始化为0)
- 遍历数组中每一个数,将其放入指定的桶中
- 按0-9的顺序又将桶中元素存回数组,覆盖之前的值
先对个位排序
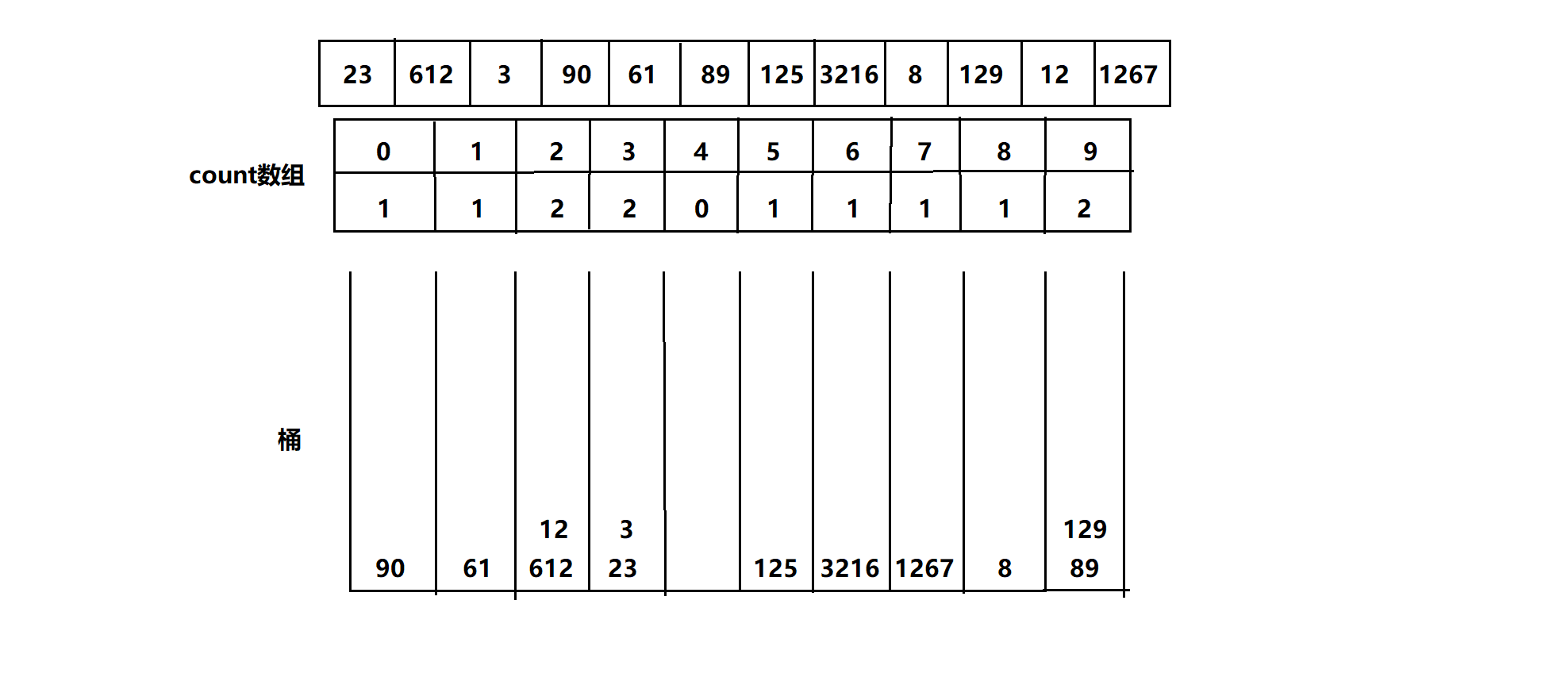
再对十位排序
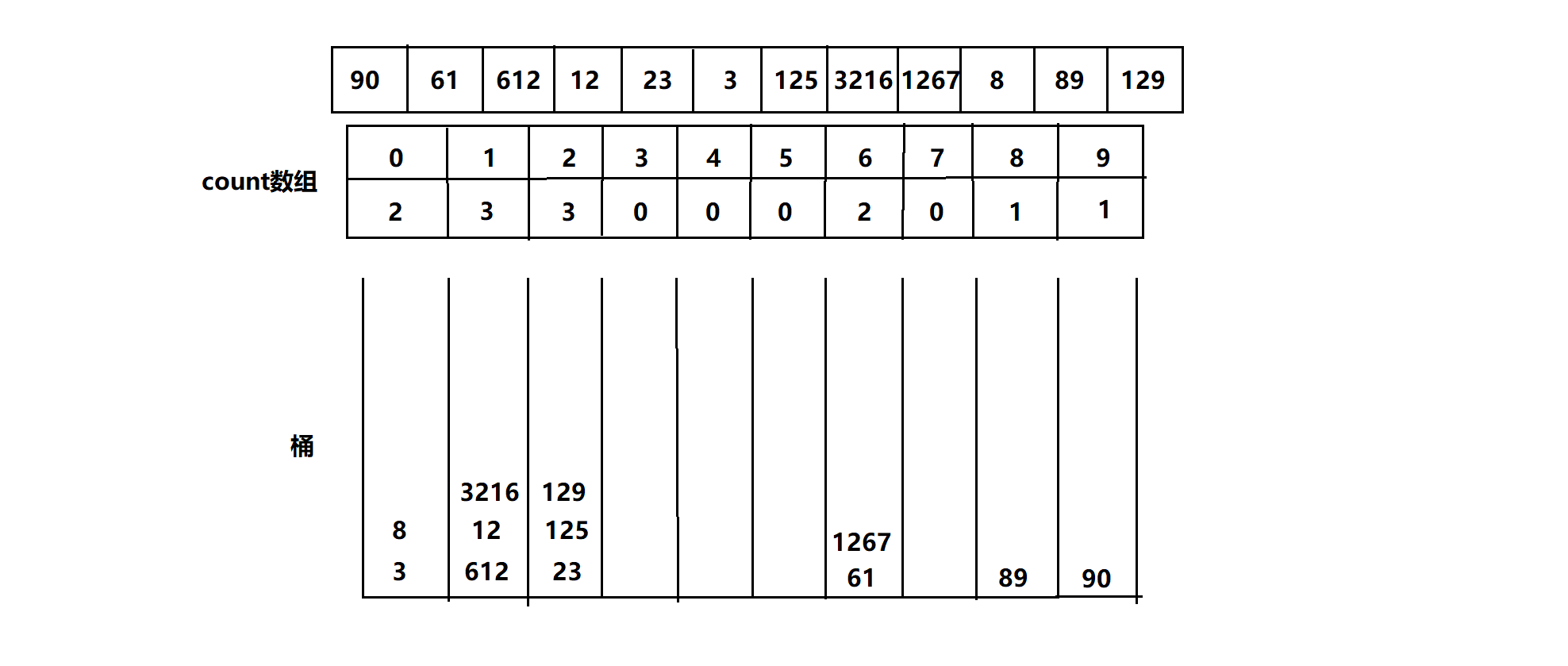
继续百位
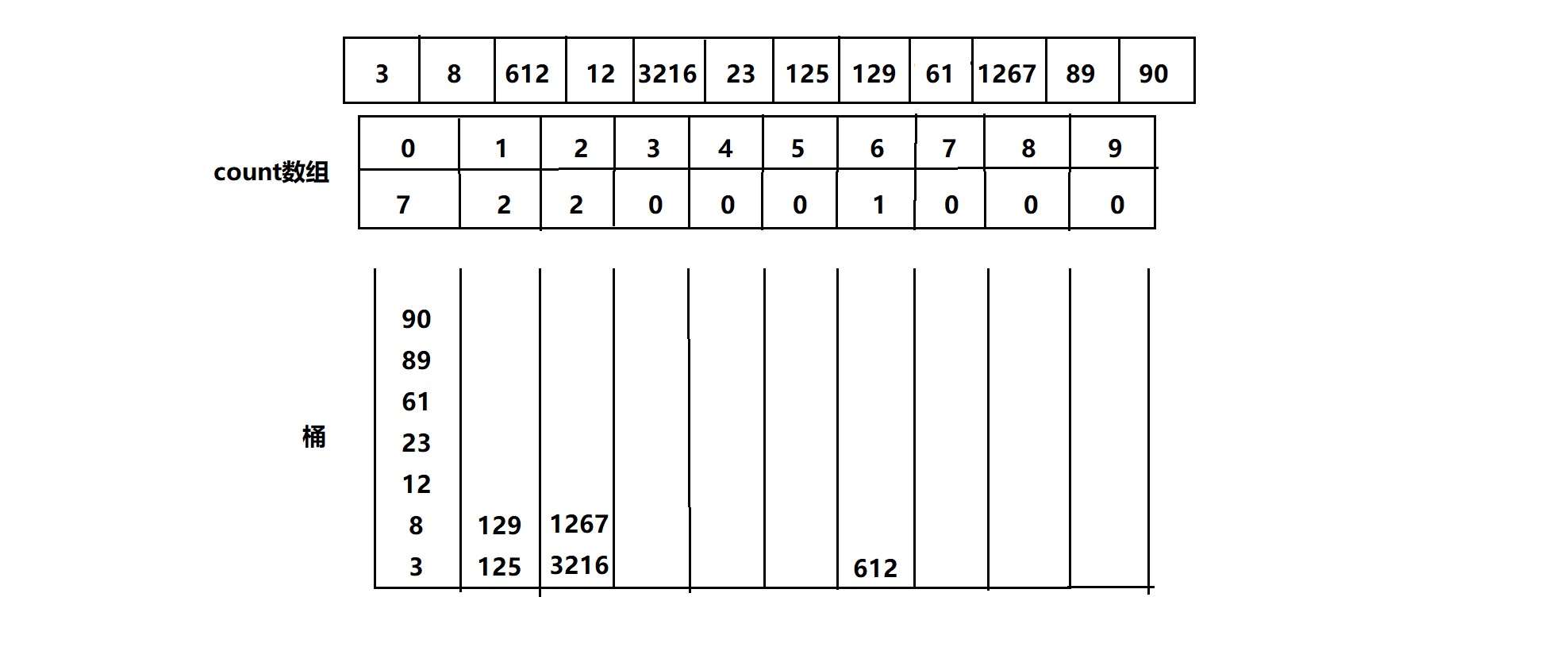
一直到最高位
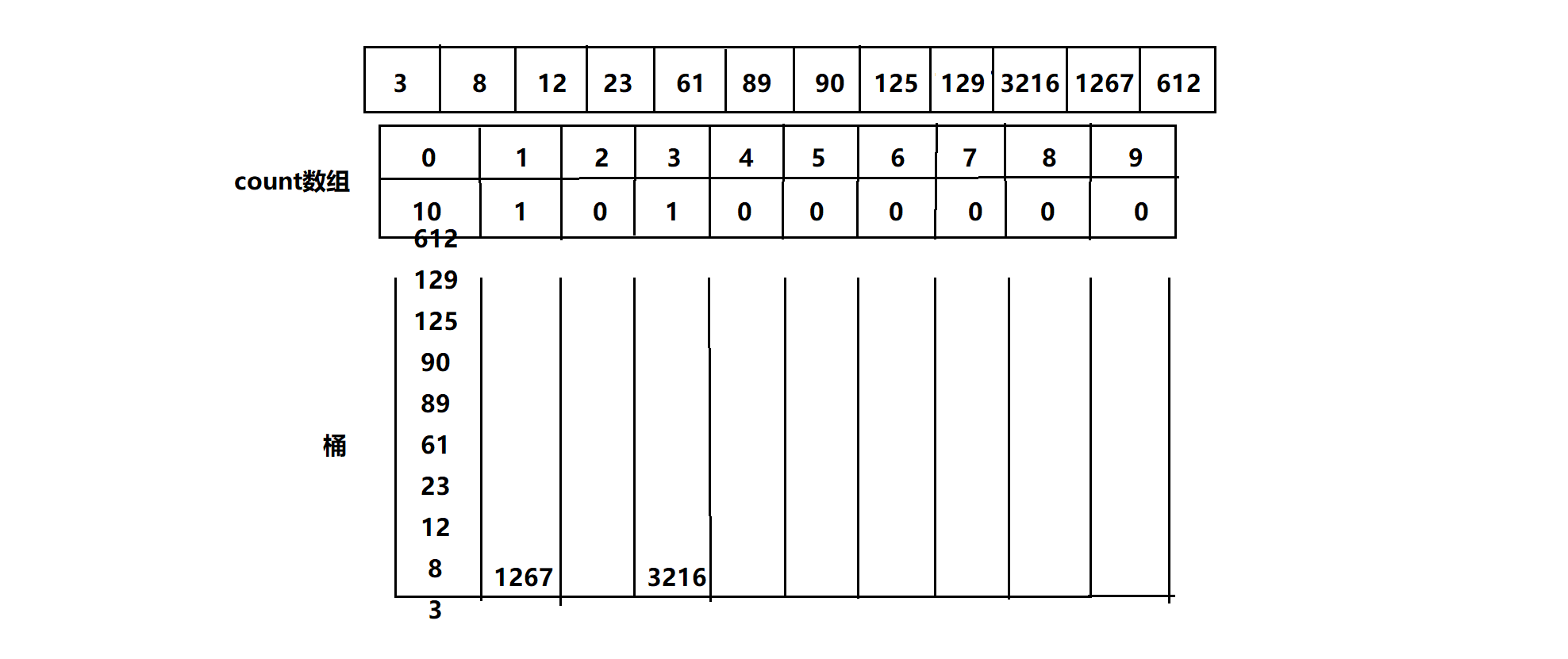
此时将桶中数字依次输出,即有序!
#include <iostream>
#include <cmath>
using namespace std;
//求数据的最大位数,可以作为对内私有的函数,先找数组中的最大数,然后求最大数的位数
int maxbit(int data[], int n)
{
int max = 0, bit = 0;
for (int i = 0; i < n; i++)
if (data[i] > max)
max = data[i];
while (max != 0)
{
max /= 10;
bit++;
}
return bit;
}
void sort(int data[], int n)
{
int bit = maxbit(data, n);
int count[10]; //统计每个桶中数的个数
int* bucket = new int[10 * n]; //二维数组,10个桶,每个桶容量最大是n,即所有元素存到一个桶中
for (int i = 1; i <= bit; i++) //循环最高位数次
{
int x = 0;
for (int p = 0; p < 10; ++p) //每次将统计桶中个数的数组清零
count[p] = 0;
for (int j = 0; j < n; j++) //遍历数组中每一个数,将其放入指定的桶中
{
int b = data[j];
//取一个数的倒数第n位的数字,就是让它除以10的n-1次方,再取10的余数
b /= pow(10, i - 1);
b %= 10;
count[b]++;
bucket[b * n + count[b]] = data[j]; //放入桶中
}
//将桶中的数据按顺序存回数组中
for (int r = 0; r < 10; r++)
{
for (int t = 1; t <= count[r]; t++)
{
data[x] = bucket[r * n + t];
x++;
}
}
}
}
int main()
{
int data[10] = { 34, 90, 12, 21, 128, 231412, 678, 123, 3, 10 };
sort(data, 10);
for (int i = 0; i < 10; ++i)
{
cout << data[i] << " ";
}
system("pause");
}