排序算法总结(未完待续)
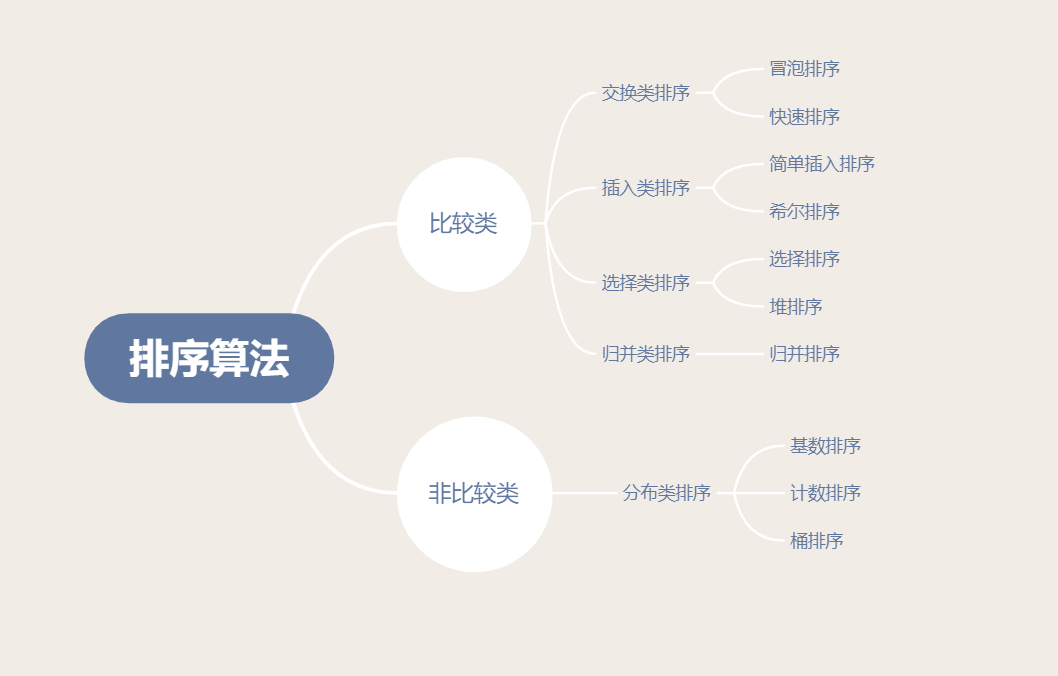
排序算法分类
冒泡排序
-
核心思想:通过把数组中相邻的两个逆序元素交换来不断减少数组中的逆序,直到全部有序
-
算法描述:
- 从当第一个元素开始,和第二个元素比较,如果逆序,则交换
- 依次往后比较每一对元素,如果逆序则交换,直到最后,最大(最小)的元素会排到末尾
- 排除掉最后一个元素,在剩下的元素中重复以上操作,直到没有逆序
-
实现:
//a是数组,n是数组的长度 void BubbleSort(int a[], int n) { //从小到大排序 for (int i = n; i > 0; i--) { //设置“门”的位置(排除掉第i+1个往后的元素) for (int j = 0; j < i-1; j++) { //从最左边开始依次比较相邻元素 if (a[j] > a[j + 1]) { //如果左边的大于右边的 //交换顺序 int tmp = a[j]; a[j] = a[j + 1]; a[j + 1] = tmp; } } } } -
动图
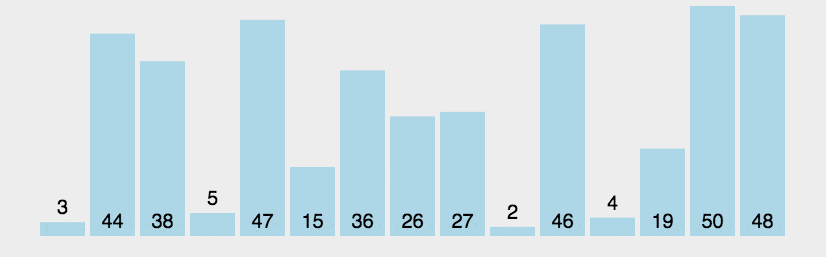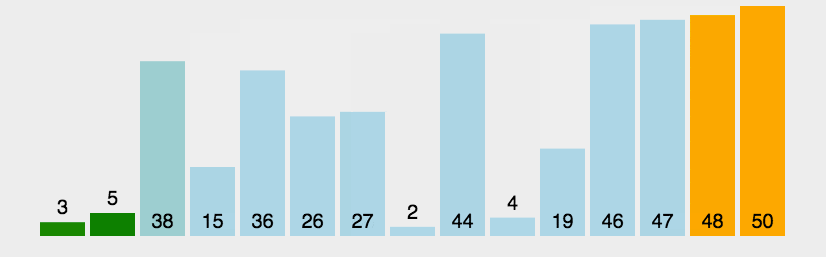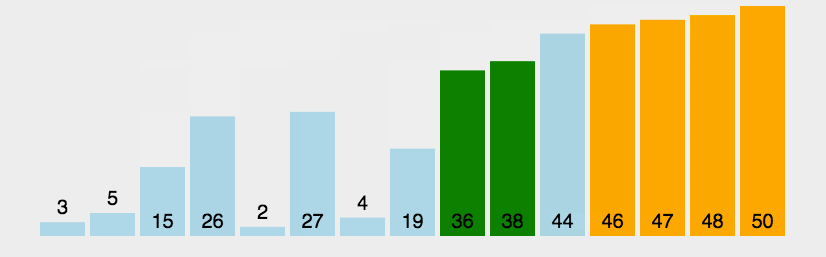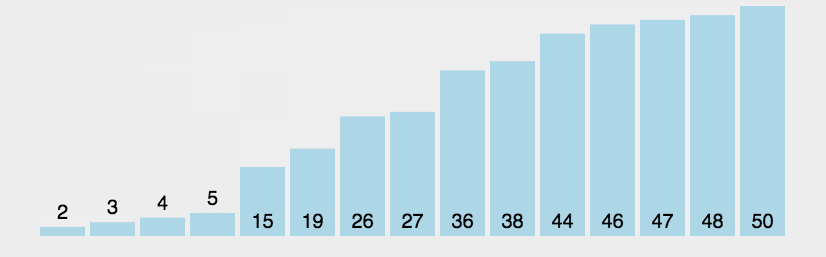
选择排序
-
核心思想:每次从无序的数组里面选出一个最小的元素,把它放到有序数组的最后面
-
算法描述:
- 从无序数组中选中最小的元素,放在排头位置,组成有序数组
- 从剩下的无序数组中选中最小的一个放在有序数组的后面
- 重复2直到无序数组为空
-
实现:
void SelectSort(int a[], int n) { for (int i = 0; i < n; i++) { //第i个之前的元素都是有序的 //从后面的无序数组中挑最小的 int min = 99999; int k = -1; //记录最小元素的下标 for (int j = i; j < n; j++) { if (min > a[j]) { min = a[j]; k = j; } } //交换 int tmp = a[i]; a[i] = a[k]; a[k] = tmp; } } -
动图
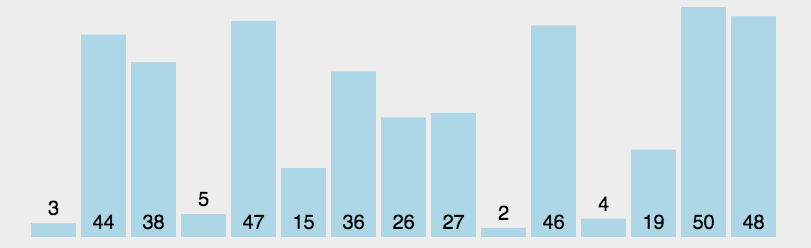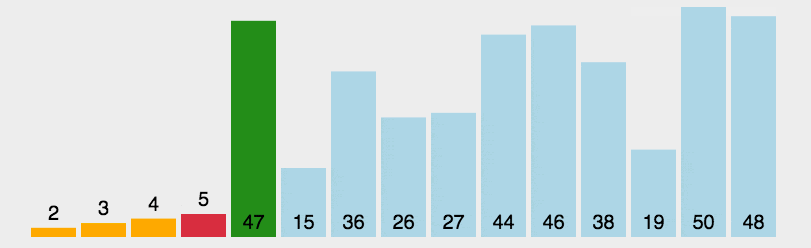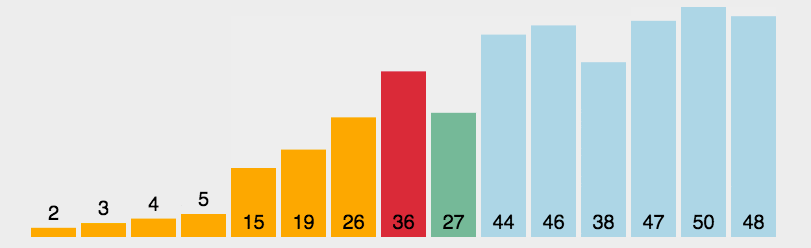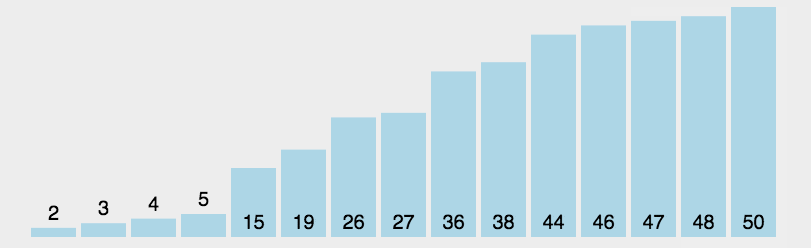
插入排序
-
核心思想: 向我们打扑克牌那样,每次选出最小的一张牌插入到排好序的牌当中
-
算法描述:
- 假定第一个元素已经排好序
- 对已排好序的序列的后一个元素,在已排好序的序列中找到它应当插入的位置,插入
- 重复2知道全部排好序
-
实现:
void InsertSort(int a[], int n) { for (int i = 1; i < n; i++) { //假定第i个以前的元素都是有序的 int tmp = a[i]; //暂存有序数列的后一个元素,给他找到位置插入 //从右往左依次和它前面的元素进行比较 int j = i - 1; while (j >=0 && a[j] > tmp) { a[j + 1] = a[j]; j--; } //插入它 a[j+1] = tmp; } } -
动图
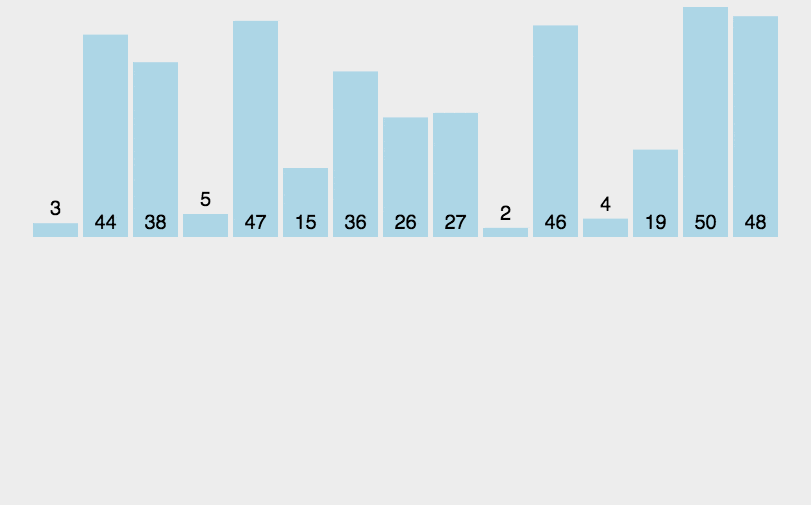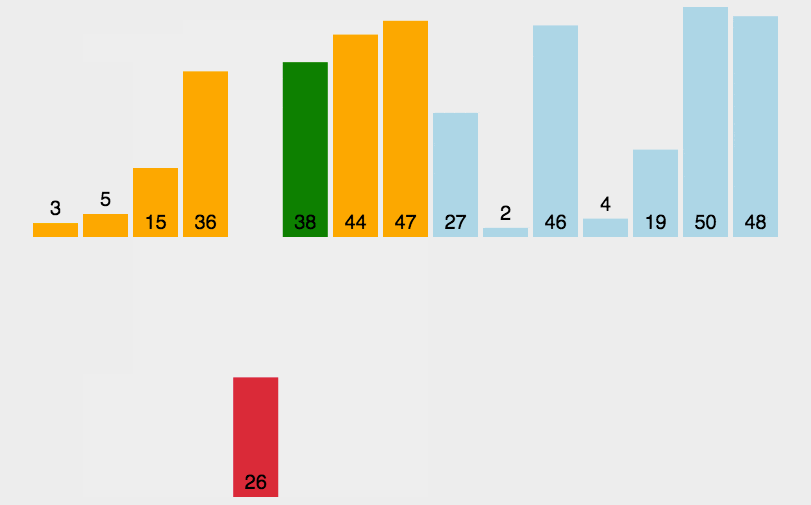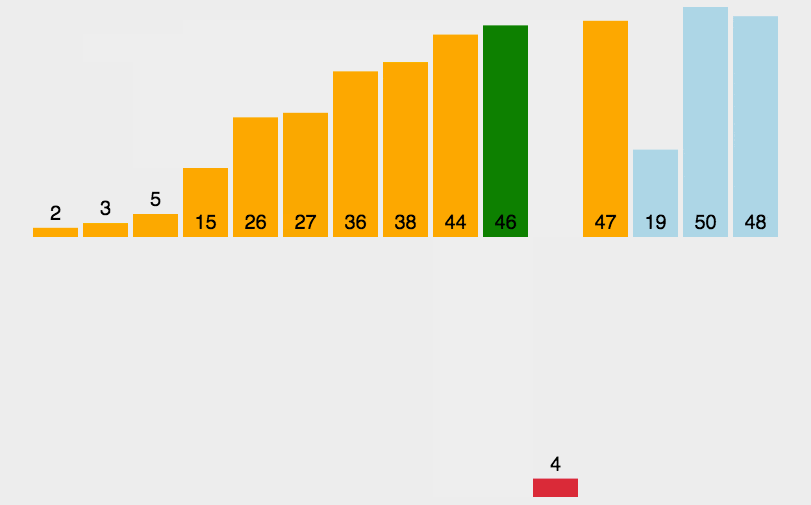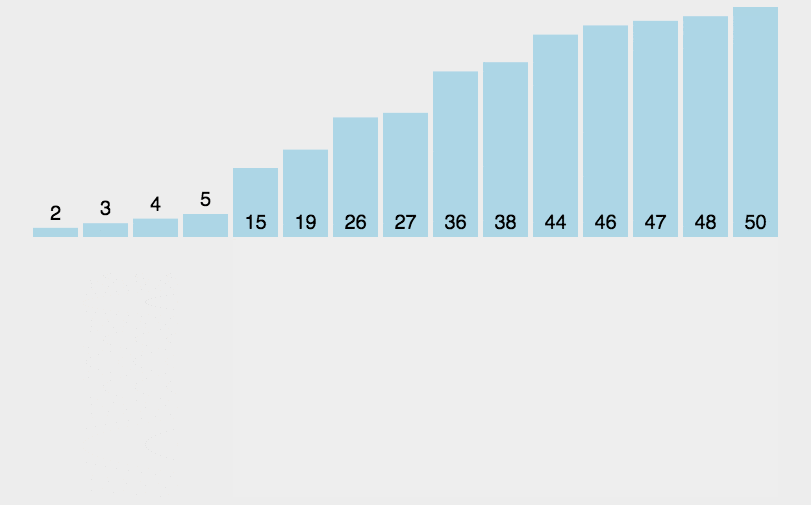
希尔排序
-
增量插入排序,是插入排序的改进版
-
核心思想:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序
-
算法描述:
- 按照增量把数组进行分组
- 对每一组内的元素实行插入排序
- 缩小增量,重复步骤1,2,直到增量为1,对整个数组实行一次插入排序
-
实现:
void ShellSort(int *a, int n) { int gap = n/2; //初始化增量数组的一半长 //增量大于0 while (gap > 0) { //按照分组进行插入排序 for (int i = gap; i < n; i++) { int tmp = a[i]; //待插入元素 int pre = i - gap; //待插入元素的前一个元素的下标 while (pre >= 0 && a[pre] > tmp) { a[pre + gap] = a[pre]; pre = pre - gap; } //插入 a[pre + gap] = tmp; } gap /= 2; //缩小增量 } } -
动图
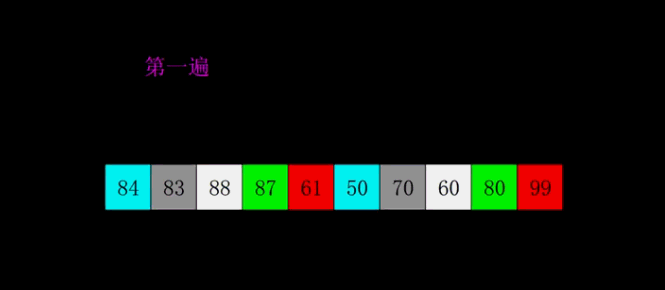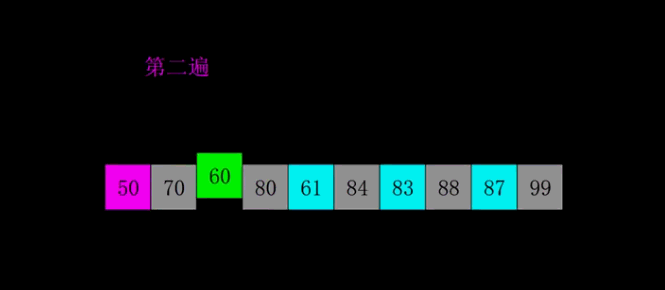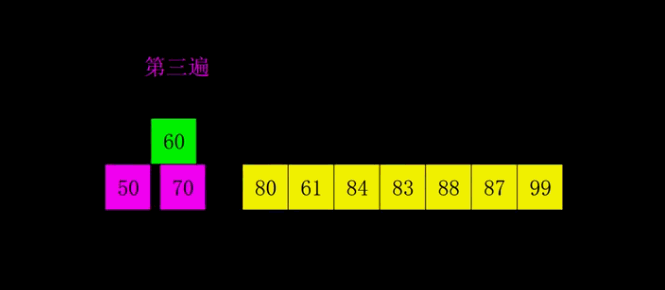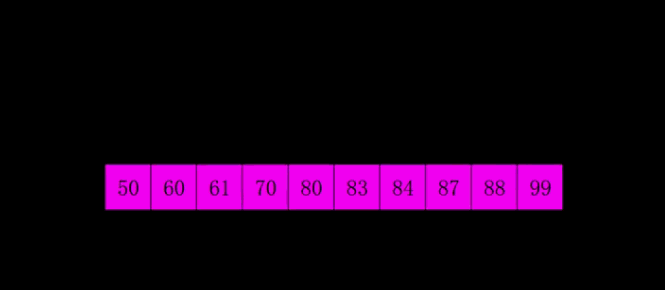
归并排序
-
核心思想:对两个有序序列进行归并很简单,所以通过分治策略,把整个序列排序分割成两两元素为一组的排序,得到每个有序小组后,又对两组间进行归并,直到全部分组归并成一个序列。
-
算法描述:
- 把长度为n的原序列分成两个长度为n/2的子序列
- 对这两个子序列分别递归进行归并排序
- 对得到的两个有序序列进行归并
-
实现:
//归并排序(递归) void MergeSort(int a[], int left, int right) { if (left < right) { int mid = (left + right) / 2; MergeSort(a, left, mid); MergeSort(a, mid + 1, right); Merge(a, left, mid, right); } } //合并两个有序数组 void Merge(int a[], int left, int mid, int right) { //开辟新数组暂存 int n = right - left + 1; int* tmp = new int[n]; int k = 0; int i = left, j = mid + 1; while (k < n) { if (i > mid) { tmp[k++] = a[j++]; } else if (j > right) { tmp[k++] = a[i++]; } else { if (a[i] < a[j]) { tmp[k++] = a[i++]; } else { tmp[k++] = a[j++]; } } } //写回原数组 for (int i = 0; i < n; i++) { a[left + i] = tmp[i]; } } -
动图:
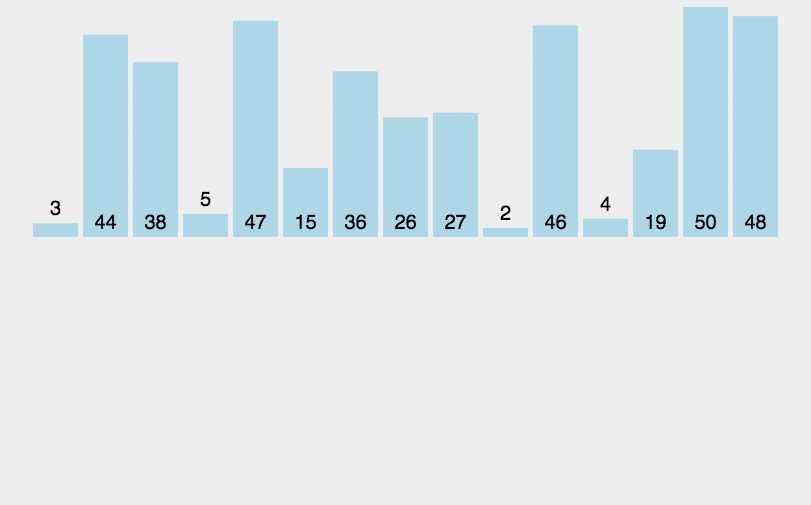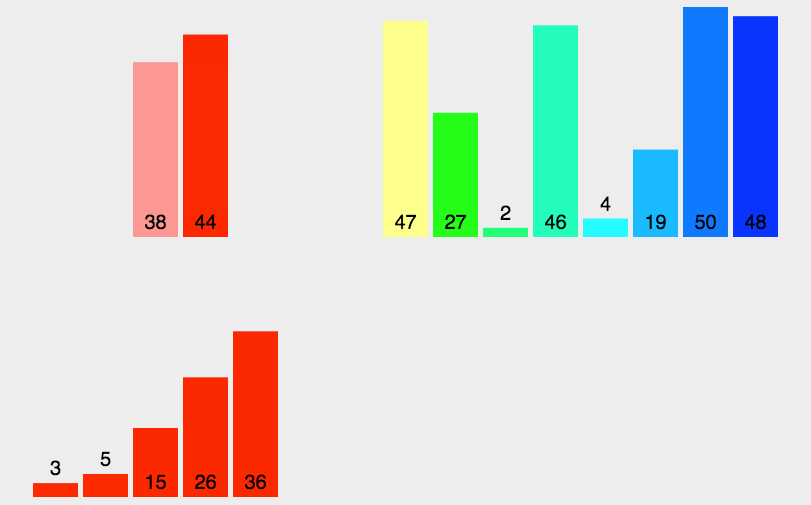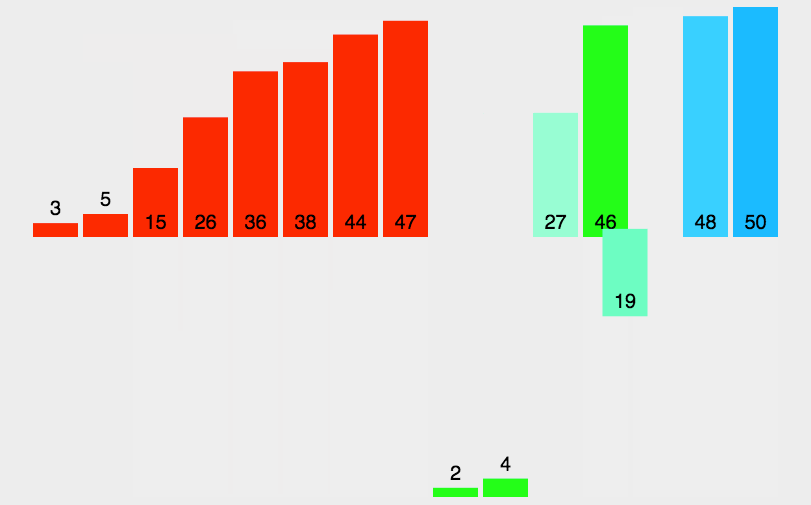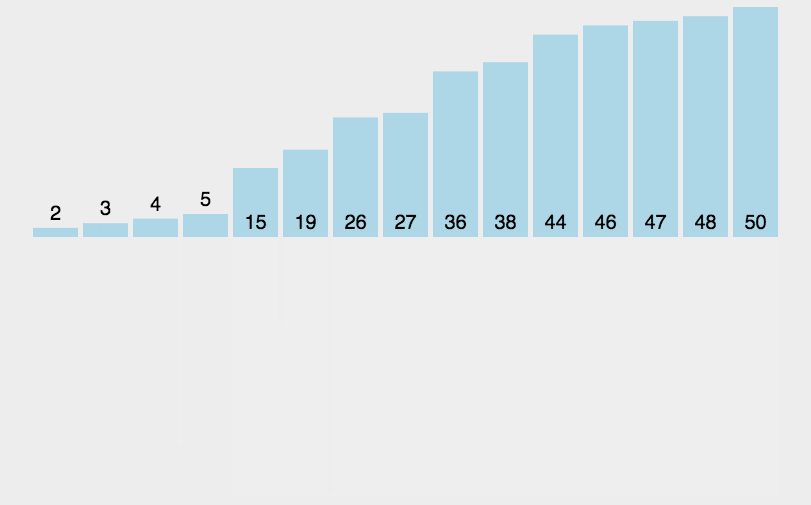
-
递归树图:
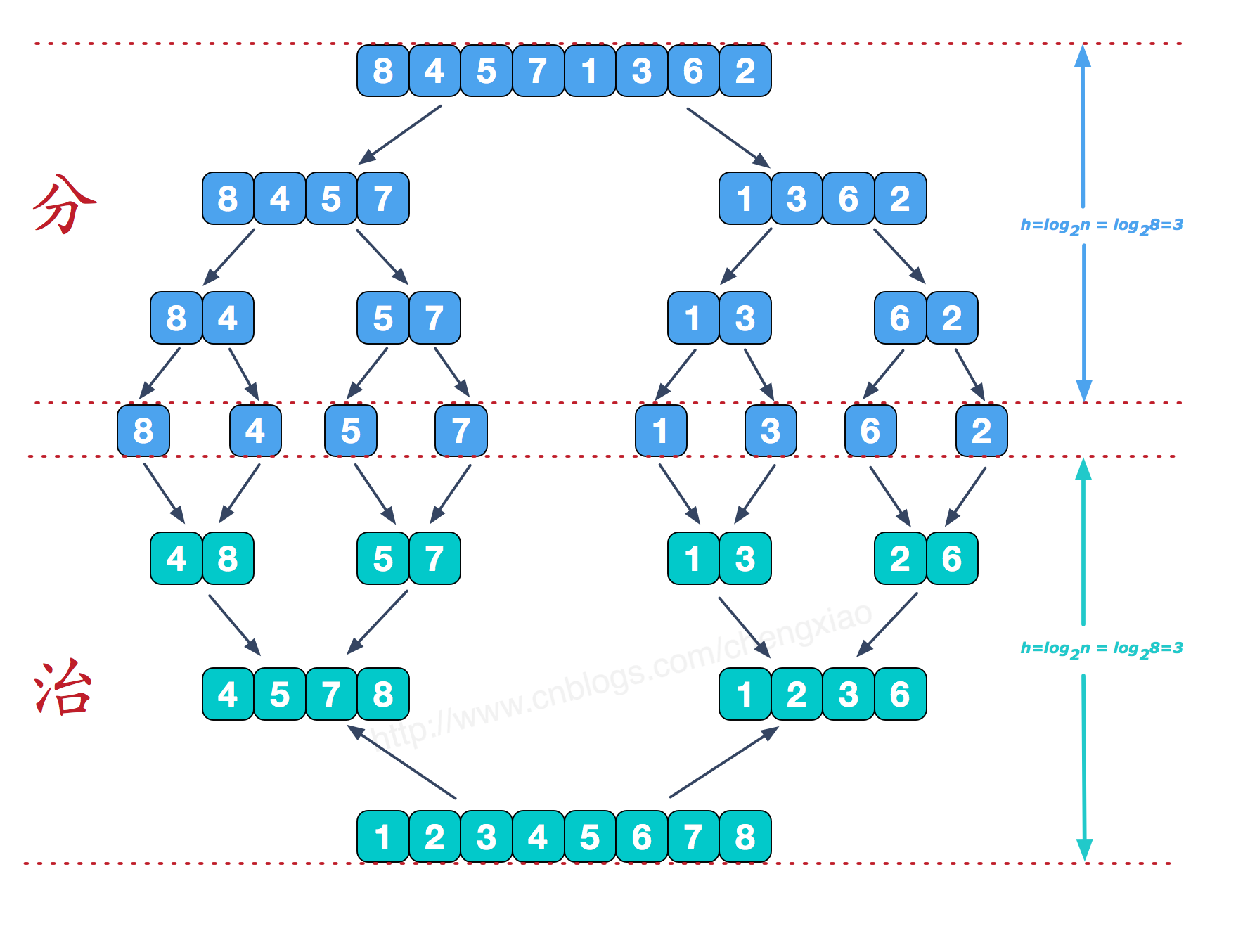
快速排序
-
核心思想:以其中一个元素为分隔点,把小于它的元素放到左边,大于他的元素放到右边。对分割后的数组执行同样操作,直到有序。
-
算法描述:
- 以排头元素为主元
- 把余下序列中小于主元的元素放到主元左边,大于它的放到右边
- 对主元左边和右边的子数组进行步骤1,2,直到子数组为空
-
实现:
int Partition(int a[], int low, int high) { int pivot = a[low]; //主元 while (low < high) { //小的放左边 while (low < high&&a[high] >= pivot) { high--; } a[low] = a[high]; //大的放右边 while (low < high&&a[low] <= pivot) { low++; } a[high] = a[low]; //相当于交换了两个元素 } //主元归位 a[high] = pivot; return low; } void QuickSort(int a[], int low, int high) { if (low < high) { //得到分割点 int pivot = Partition(a, low, high); //递归调用 QuickSort(a, low, pivot - 1); QuickSort(a, pivot + 1, high); } } -
图解:
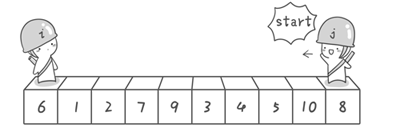

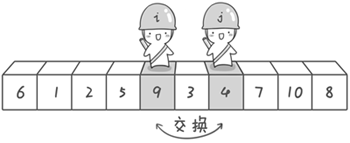

堆排序
-
基本思想: 堆是一种有特殊性质的树形结构,一种是父亲结点一定会比儿子结点大(大根堆),另一种是父亲结点一定会比儿子结点小(小根堆)。根据这种性质,我们就可以在维护这样的堆的同时,一次从中摘取出最大(最小)元素就可以完成排序了。
-
堆示意图:
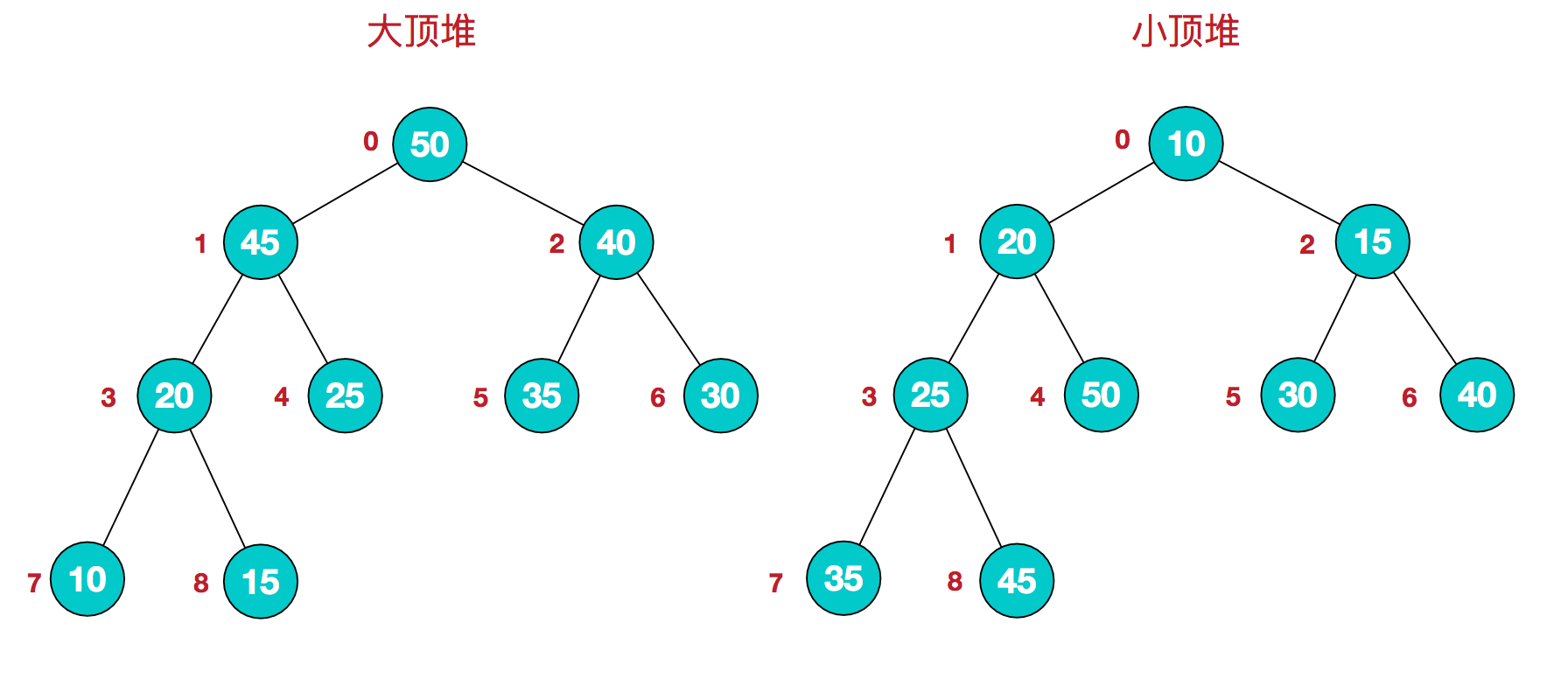

-
算法描述:
- 生成一个大根堆
- 交换根和堆尾元素(把最大值放到有序数组的排头)
- 排除掉堆的末尾元素,重复1,2直到堆中只剩下一个元素
-
实现:
void heapfiy(int a[], int i, int n) { //堆调整,i是开始调整的位置,n是要调整的数组的长度 //从i开始向下交换 while (2 * i + 1 < n) { //还有儿子 int left = 2 * i + 1; //左儿子 int right = 2 * i + 2; //右儿子 if (right < n) { //可能没有右孩子 //找到较大的儿子结点 if (a[left] < a[right]) { left = right; } } //若儿子比i大,则交换 if (a[i] < a[left]) { swap(a[left], a[i]); i = left; } else { //没有逆序了,不需要调整,退出 break; } } } //建堆 void buildHeap(int a[], int n) { //n是数组长度 //从第一个非叶子结点开始,一直到根 for (int i = n / 2; i >= 0; i--) { heapfiy(a, i, n); } } //堆排序 void HeapSort(int a[], int n) { //建堆 buildHeap(a, n); //排序 for (int i = n - 1; i >= 0; i--) { //交换头尾两个元素 swap(a[0], a[i]); //重新调整堆 heapfiy(a, 0, i); } } -
动图:
