神必博主的沙雕前言
参考文献:
概念明晰
所谓 ( ext{1D/1D}) 动态规划, 指的是状态数和单状态决策数都是 (O(n)) 的动态规划方程, 暴力求解的时间复杂度为 (O(n^2))。
四边形不等式
(f[i] = min/max_{j in [1,i-1]} { f[j] + w(j,i) }) 形式及四边形不等式的定义
下面只考虑取 (min)。
决策单调性是指对于 (a<b<c<d), 若对于 (c) 从 (b) 转移来不比从 (a) 转移来差, 那么对于 (d) 从 (b) 转移来就不比从 (a) 转移来差, 即
那么显然对于 (w) 函数来说, 如果满足这个等式:(-w(b,c)+w(b,d) le -w(a,c)+w(a,d)), 就可以使得 ((1)) 成立。
将此等式转化一下, 就得到了 四边形不等式:
对于 (max) 的情况也差不多, 只是等号的方向变了一下。
可以看出四边形不等式与决策单调性有着很亲密的关系。
四边形不等式的判定与性质
还是以 (min) 来说明。
有一个与四边形不等式等价的式子, 若函数 (w) 对于任意 (a<b), (w(a,b)+w(a+1,b+1) le w(a+1,b) + w(a,b+1)), 则函数 (w) 满足四边形不等式。
不会证。
3道练证明的例题
HNOI2008玩具装箱
CF868F
太简单了不写了。
诗人小G
很显然的 (DP) 方程:
其中, (w(j,i) = Bigg| [i-(j+1)+1-1] + sum_{k=j+1}^i a[k] -L Bigg|^P), 若记 (s[i] = sum_{k=1}^i a[k]), 则 (w(j,i) = Bigg|i-j-1+s[i]-s[j]-L Bigg|^P) 。
如果 (w) 满足四边形不等式, 那么这个 (DP) 方程就满足决策单调性。
只需证明 (w(i,j) + w(i+1,j+1) le w(i+1,j) + w(i,j+1)) 。
展开, 得到
设 (u = i-j-2+s[i]-s[j+1]-L), (v = i-j-1+s[i]-s[j]-L), 则原式变成
由于 (u<v),这也就等价于证明 (|x|^P - |x+z|^P ;;(zin[1,+infty])) 单调不增。
分类讨论:
- (x in [0,+infty])
(|x|^P - |x+z|^P = x^P - (x+z)^P)
导数是 (Px^{P-1} - P(x+z)^{P-1})
显然是小于等于 (0) 的。
2.(x in (-infty, 0)) 且 (P) 为偶数
(|x|^P - |x+z|^P = x^P - (x+z)^P)
导数依然是 (Px^{P-1} - P(x+z)^{P-1}), 由于 (P-1) 是奇数, 所以依然是小于等于 (0) 的。
3.(x in (-infty, 0)) 且 (P) 为奇数, (x+z ge 0)
(|x|^P - |x+z|^P = -x^p - (x+z)^P)
导数为 (-Px^{P-1} - P(x+z)^{P-1})
显然是小于等于 (0) 的。
4.(x in (-infty, 0)) 且 (P) 为奇数, (x+z < 0)
(|x|^P - |x+z|^P = -x^p + (x+z)^P)
导数为 (-Px^{P-1} + P(x+z)^{P-1})
显然 (x+z ge x), 但 (x+z) 为负数, 大于 (x) 的负数中没有绝对值比 (x) 大的, 故这个导数也是小于等于 (0) 的。
Q.E.D.
可以放心用决策单调性优化了。
实现方法
二分栈
从左往右扫, 用扫到的状态更新它后面的状态。由于一个状态只会从它左边的状态转移来, 所以此算法的正确性得以保证。
由于决策单调性, 每次遭到更新的状态集一定是序列的一段后缀, 可以快速计算。
具体实现的时候用栈维护几个连续的段, 每个段记录其左端点,就可以描绘出整个转移序列。每扫到 (i) 的时候, 先把 (i) 的 (dp) 值计算出来, 再用其更新后面状态的转移。
实现的时候有几个关键点, 决定着程序的常数。
以 诗人小G 这道题为例。
首先是一个糟糕的实现, 虽然能过, 但是耗时并不优秀。
(由于没有写注释, 观看的时候只看代码的丑陋程度就行了)
//对于每段不仅维护了左端点还维护了右端点, 并且加入了繁杂的分类讨论
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int n,stn,mdzz;
char s[maxn][35];
int S[maxn];
int tot, q[maxn], l[maxn], r[maxn];
long double f[maxn];
long double ksm(long double a, int b) {
long double res = 1;
for(;b;b>>=1, a*=a)
if(b&1) res *= a;
return res;
}
long double val(int pr, int nx) {
long double res = f[pr];
// nx - pr + S[nx] - S[pr] - stn
res += ksm(abs(S[nx]-S[pr] + (nx-pr-1) - stn), mdzz);
return res;
}
int pre[maxn];
void fuck(int i)
{
int L=1, R=tot;
while(L!=R) {
int mid = (L+R+1) >> 1;
if(l[q[mid]] > i) R = mid-1;
else L = mid;
}
int pr = q[L];
pre[i] = pr;
f[i] = val(pr, i);
//cout << pr << ' ';
}
void print(int x)
{
if(!x) return;
int pr = pre[x];
print(pr);
for(int i=pr+1; i<x; ++i) printf("%s ", s[i]);
printf("%s
", s[x]);
}
int main() {
int t;
cin >> t;
while(t--)
{
scanf("%d%d%d", &n, &stn, &mdzz);
for(int i=1; i<=n; ++i) {
scanf("%s", s[i]);
S[i] = S[i-1] + strlen(s[i]);
}
q[tot=1] = 0;
l[0]=1, r[0]=n;
for(int i=1; i<n; ++i) {
fuck(i);
int L=1, R=tot;
while(L!=R) {
int mid = (L+R+1) >> 1;
if(val(i,l[q[mid]]) < val(q[mid],l[q[mid]])) R = mid-1;
else L=mid;
}
int nowb = L;
L=l[q[nowb]], R=r[q[nowb]];
while(L!=R) {
int mid = (L+R) >> 1;
if(val(i, mid) < val(q[nowb], mid)) R=mid;
else L=mid+1;
}
int nowp = L;
if(val(i, nowp) > val(q[nowb], nowp)) ++nowp;
if(nowp == n+1) continue;
while(l[q[tot]] > nowp) --tot;
if(l[q[tot]] == nowp) q[tot]=i, l[i] = nowp, r[i] = n;
else {
r[q[tot]] = nowp-1;
q[++tot] = i;
l[i] = nowp;
r[i] = n;
}
}
fuck(n);
if(f[n] <= 1e18) {
cout << (long long)f[n] << '
';
//print
print(n);
}
else cout << "Too hard to arrange
";
cout << "--------------------
";
}
return 0;
}
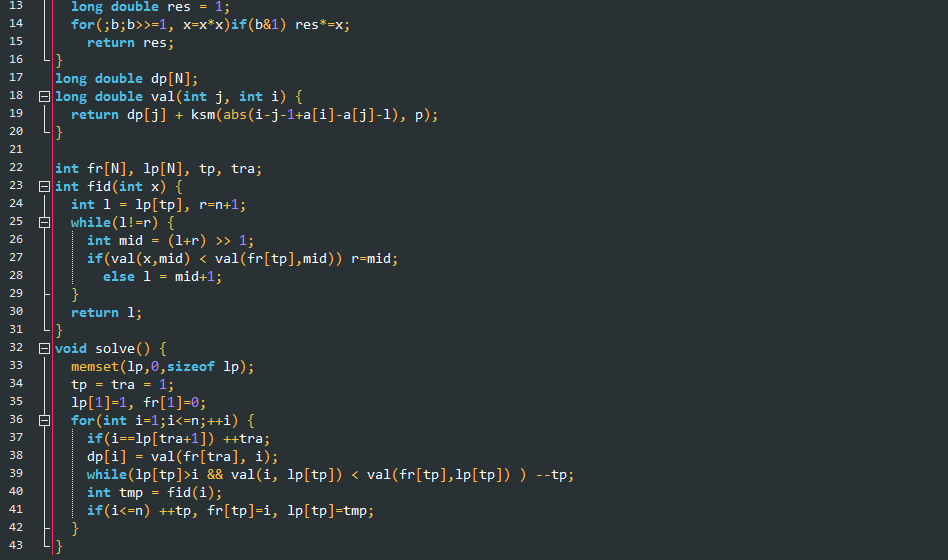
接下来是比较优美的实现。
//这份实现充分体现了二分栈算法的特性, 理解这份实现对更好理解二分栈算法有帮助
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,l,p;
char s[N][33];
int a[N];
long double ksm(long double x, int b) {
long double res = 1;
for(;b;b>>=1, x=x*x)if(b&1) res*=x;
return res;
}
long double dp[N];
long double val(int j, int i) {
return dp[j] + ksm(abs(i-j-1+a[i]-a[j]-l), p);
}
int fr[N], lp[N], tp, tra;
int fid(int x) {
int l = lp[tp], r=n+1;
while(l!=r) {
int mid = (l+r) >> 1;
if(val(x,mid) < val(fr[tp],mid)) r=mid;
else l = mid+1;
}
return l;
}
void solve() {
memset(lp,0,sizeof lp);
tp = tra = 1;
lp[1]=1, fr[1]=0;
for(int i=1;i<=n;++i) {
if(i==lp[tra+1]) ++tra;
dp[i] = val(fr[tra], i);
while(lp[tp]>i && val(i, lp[tp]) < val(fr[tp],lp[tp]) ) --tp;
int tmp = fid(i);
if(i<=n) ++tp, fr[tp]=i, lp[tp]=tmp;
}
}
int pre[N];
void Prin(int i) {
if(!i) return;
Prin(pre[i]);
for(int j=pre[i]+1;j<i;++j) printf("%s ",s[j]);
printf("%s
", s[i]);
}
void print() {
if(dp[n]>1e18) puts("Too hard to arrange");
else {
cout << (long long)dp[n] << '
';
// 这里偷懒写了大常数 owo
// awsl
int r = n;
while(tp) {
while(r>=lp[tp]) pre[r--]=fr[tp];
--tp;
}
Prin(n);
}
}
int main() {
int t; cin>>t; while(t--) {
memset(a,0,sizeof a);
scanf("%d%d%d",&n,&l,&p);
for(int i=1;i<=n;++i) {
scanf("%s",s[i]); a[i]= a[i-1] + strlen(s[i]);
}
a[n+1] = a[n] + 1;
solve();
print();
puts("--------------------");
}
return 0;
}
啊这, 还是两格空格缩进好看, 完全不一样的feel啊。
分治
有点难用, 不写了。