“我找到好办法了!”
没有想到,说话的人竟然是磁盘!
进程调度器瑟瑟的说:“你有方法?还是算了吧,我怕用你的方法操作系统要乱套了。”
磁盘委屈的道:“不就是刚刚冤枉你了吗,这么小气干什么!再说了,这个方法不是我想出来的,是我从文件里找到的。”
操作系统挑了挑眉毛:“哦?你找到什么文件了,让大家也瞅瞅?”
磁盘嗡嗡的转起来,很快就把文件取出来了。
“当当当当~ 这可是大师 Dijkstra 的论文,他引入了一个全新的变量类型——信号量(semaphore)。然后还为信号量设置了两种操作,P(proberen,检测) 和 V(verhogen,增量) 。”
”说清楚点啊,信号量是怎么个用法啊?“进程急切的问道。
“别急,让我接着看。。。Dijkstra 提出,P操作是检测信号量是否为正值,如果不是,就阻塞调用进程。 V操作能唤醒一个阻塞进程,让他恢复执行 。具体点的话就是这样: “
// S 为信号量
P(s):
{
S = S - 1
if (S < 0)
{
调用该 P 操作的进程阻塞,并插入相应的阻塞队列;
}
}
// S 为信号量
V(s):
{
S = S + 1
if (S <= 0)
{
从等待信号量 S 的阻塞队列里唤醒一个进程;
}
}
内存仔细看了代码,说:”这个实现也要求是原子操作诶,Dijkstra 这个方法很有趣啊。“
进程蒙圈了:“我怎么完全看不懂啊?内存你给我讲讲呗。”
“好,我就用最简单的一组线程举例子了:
// 线程 A,B,C , S = 1
...
P(S) //S = S - 1 若 S < 0 ,阻塞等待
购票操作
V(S) //S = S + 1 若 S <= 0, 表明有线程阻塞了,得唤醒其中一个
...
这里的 「购票操作」 就是我们要保护的临界区,我们要保证一次只能有一个线程进入。那我们就把 S 的初始值设为 1 。当线程 A 第一个调用 P(S) 后,S 的值就变成了 0 ,A 成功进入临界区。在 A 出临界区之前,线程 B 如果调用 P(S), S 就变成 -1 ,满足 S < 0 的判断条件,线程 B 就被阻塞了。等 A 调用 V(S) 后,S 的值又变成 0 ,满足 S <= 0,就会把线程 B 唤醒,B 就能进入临界区了。“
进程恍然大悟:“原来是这样,看起来和二元锁差不多啊,但是不用忙等待了。”
内存神秘一笑:“信号量能做的可不止这些,你想想看,要是我把 S 的初始值设为 2 ,会发生什么?”
“一次能有两个线程访问临界区!”进程这次反应快多了:“也就是说 S 的初始值可以控制有多少个线程进入临界区,太厉害了!”
tobe 注:从信号量的值能看出还有多少个进程能进入临界区,如果为负数,表明有 x 个进程因为调用 P(S) 而被阻塞
“没错,所以说信号量是一个很灵活的并发机制。而且信号量还有另一个厉害的用处:

你看这两个进程有什么特别的地方?“
“emmmm,这个嘛,进程 P2 的 V 操作居然放在 P 操作的前面,而且两个操作的信号量还不是同一个。”
“没错,这样使用信号量,能让两个进程做到同步。你看,如果 P1 运行到 P(S1),他是不是会阻塞?”
进程认真一看,说:“没错诶,S1 初始值是 0,P1 肯定得停在这一句。让我再看看,,,如果 P1 想接着运行,就得等 P2 调用 V(S1) 把他唤醒。”
“是的,这就是同步——运行快的 P1 必须在这里停下来等 P2 运行到指定位置。两个进程的执行顺序就是这样:
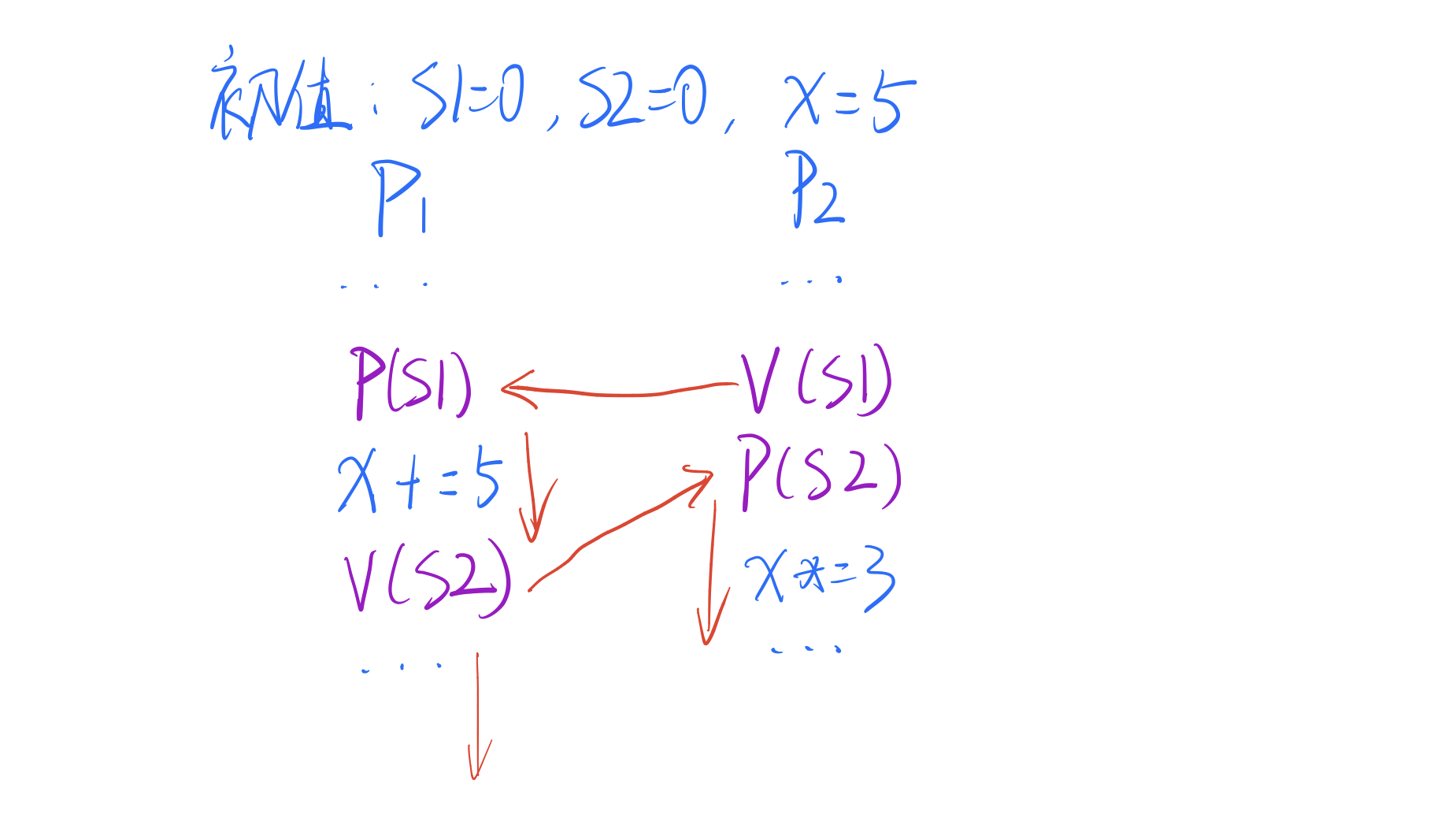
也就是说 x 最终的值必然是 30,而不可能是 20。在信号量的帮助下,这两个进程达成了同步。“
进程由衷的感叹:“信号量实在是太强大了!咱们以后就用信号量来解决互斥的问题吧!”
tobe 注:在 Linux 里提供了信号量和互斥量(也就是二元锁)这两种主要机制实现互斥,不过 Linux 的信号量功能要比文章里讲得复杂得多,「UNIX 环境高级编程」这本书里写到「。。。三种特性造成了这种并非必要的复杂性」,对于一般的互斥操作,还是建议使用互斥锁(当然是阻塞而非忙等待)。稍微复杂点的锁还有「读写锁」,以后有机会再讲吧~
觉得我写的还不错的话,就点个赞吧!