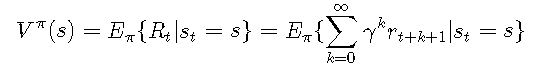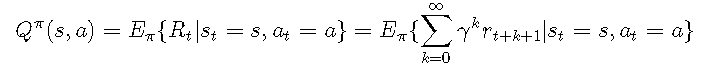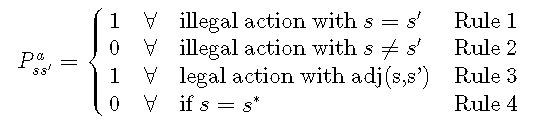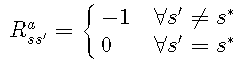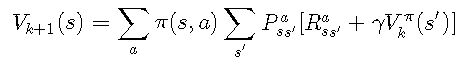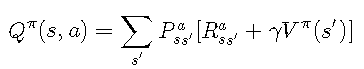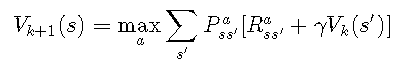python中使用马尔可夫决策过程(MDP)动态编程来解决最短路径强化学习问题

 

原文链接：http://tecdat.cn/?p=11105

 

在强化学习中，我们有兴趣确定一种最大化获取奖励的策略。假设环境是马尔可夫决策过程  （MDP）的理想模型  ，我们可以应用动态编程方法来解决强化学习问题。

在这篇文章中，我介绍了可以在MDP上下文中使用的三种动态编程算法。为了使这些概念更容易理解，我在网格世界的上下文中实现了算法，这是演示强化学习的流行示例。

在开始使用该应用程序之前，我想快速提供网格世界上后续工作所需的理论背景。

MDP的关键强化学习术语

以下各节解释了强化学习的关键术语，即：

• 策略：  代理应在哪种状态下执行哪些操作
• 状态值函数：  每个州关于未来奖励的期望值
• 行动价值函数：  在特定状态下针对未来奖励执行特定行动的预期价值
• 过渡概率：  从一种状态过渡到另一种状态的概率
• 奖励功能：  代理在状态之间转换时获得的奖励

状态值函数

给定策略ππ，状态值函数Vπ（s）Vπ（s）将每个状态ss映射到代理在此状态下可获得的预期收益：

​

式中，stst表示时刻tt的状态。参数γ∈[0,1]γ∈[0,1]称为  折扣因子。它决定了未来奖励的影响。 

动作值函数

给定策略ππ，动作值函数Qπ（s，a）Qπ（s，a）确定在状态ss中执行动作aa时的预期奖励：

​

转移概率

在状态ss中执行动作aa可以将代理转换为状态s's'。通过Pass'Pss'a描述发生此过渡的可能性。

奖励函数

奖励函数Rass'Rss'a指定当代理通过动作aa从状态ss过渡到状态s's'时获得的奖励。

Gridworld中的三种基本MDP算法的演示

在本文中，您将学习如何在网格世界中为MDP应用三种算法：

1. 策略评估：  给定策略ππ，与ππ相关的价值函数是什么？
2. 策略迭代：  给定策略ππ，我们如何找到最佳策略π∗π∗？
3. 值迭代：  如何从头开始找到最佳策略π∗π∗？

在gridworld中，代理的目标是到达网格中的指定位置。该代理可以向北，向东，向南或向西移动。这些动作由集合{N，E，S，W} {N，E，S，W}表示。请注意，代理始终知道状态（即其在网格中的位置）。

 网格中存在一些壁，代理无法通过这些壁。 

基本的Gridworld实施

我已经以面向对象的方式实现了gridworld。以下各节描述了我如何设计地图和策略实体的代码。

 Gridworld地图

为了实现gridworld，我首先要做的是代表地图的类。我定义了以下格式来表示各个网格单元：

• # 指示墙壁
• X 表明目标
• 空白表示空块

依靠这些符号， 构造  了下面的map ：

###################
#                X#
#   ###########   #
#   #         #   #
#   # ####### #   #
#   # #     # #   #
#     #  #  #     #
#        #        #
#                 #
###             ###
#                 #
###################

  

我实现了  MapParser，它生成一个  Map对象。地图对象控制   对gridworld 单元的访问。单个单元格子类定义特定单元格的行为，例如空单元格，墙和目标单元格。可以使用其行和列索引来标识每个单元格。

通过此设置，可以方便地加载地图：

parser = MapParser()
gridMap = parser.parseMap("../data/map01.grid")

载入 

对于强化学习，我们需要能够处理一个策略π（s，a）π（s，a）。在gridworld中，每个状态ss代表代理的位置。这些动作将代理移动到四个地理方向之一。我们将使用以下符号将策略映射到地图上：

• N为动作 GO_NORTH
• E为行动 GO_EAST
• S为动作 GO_SOUTH
• W为行动 GO_WEST

未知符号被映射到  NONE 操作  ，以获得完整的策略。

使用这些定义，我定义  了以下策略：

###################
#EESWWWWWWWWWWWWWX#
#EES###########SWN#
#EES#EEEEEEEES#SWN#
#EES#N#######S#SWN#
#EES#N#SSWWW#S#SWN#
#EEEEN#SS#NN#SWSWN#
#EENSSSSS#NNWWWWWN#
#EENWWWWEEEEEEEEEN#
###NNNNNNNNNNNNN###
#EENWWWWWWWWWWWWWW#
###################

请注意，策略文件保留了围墙和目标单元，以提高可读性。该政策的制定有两个目标：

1. 代理应该能够达到目标。 对于未实现此属性的策略，策略评估将不会给出合理的结果，因为永远不会获得目标回报。
2. 该策略应该不是最理想的。这意味着在某些状态下，业务代表没有采取最短的路径达到目标。这样的策略使我们可以看到尝试改进初始策略的算法的效果。

为了加载该策略，我实现了一个  策略解析器，该解析器将策略存储为  策略对象。使用这些对象，我们可以像这样加载初始策略：

policyParser = PolicyParser()
policy = policyParser.parsePolicy("../data/map01.policy")

策略对象具有用于建模π（s，a）π（s，a）的功能：

def pi(self, cell, action):
    if len(self.policy) == 0:
        # no policy: try all actions (for value iteration)
        return 1

    if self.policyActionForCell(cell) == action:
        # policy allows this action
        return  1
    else:
        # policy forbids this action
        return 0

强化学习的准备

为了准备实施强化学习算法，我们仍然需要提供过渡和奖励功能。

过渡函数

要定义转换函数Pass'Pss'a，我们首先需要区分非法行为和法律行为。在gridworld中，有两种方法可以使动作不合法：

1. 如果该动作会使代理脱离网格
2. 如果该动作会使代理人陷入困境

这为我们提供了转换函数的第一条规则：

1. When an action is illegal, the agent should remain in its previous state.

此外，我们还必须要求：

2. When an action is illegal, transitions to states other than its previous state should be forbidden.

 当然，状态转换对于所选动作必须有效。由于每个动作仅将代理移动一个位置，因此建议状态s's'必须在与状态ss相邻的单元格中具有代理：

3. Only allow transitions through actions that would lead the agent to an adjacent cell.

对于此规则，我们假设有一个谓词adj（s，s'）adj（s，s'）来指示主体从ss到s's'的过渡是否涉及相邻单元格。

最后，一旦达到目标状态s ∗ s ∗，我们就不希望代理再次离开。为了说明这一点，我们引入了最终规则：

4. Don't transition from the goal cell.

基于这四个规则，我们可以定义转换函数如下：

​

所提供的Python实现  getTransitionProbability 并不像数学公式那样明确 ：

def getTransitionProbability(self, oldState, newState, action, gridWorld):
    proposedCell = gridWorld.proposeMove(action)
    if proposedCell is None:
        # Rule 1 and 2: illegal move 
        return transitionProbabilityForIllegalMoves(oldState, newState)
    if oldState.isGoal():
        # Rule 4: stay at goal
        return 0
    if proposedCell != newState:
        # Rule 3: move not possible
        return 0
    else:
        # Rule 3: move possible
        return 1

请注意，它  proposeMove 模拟了操作的成功执行，并返回了代理的新网格单元。

奖励函数

在gridworld中，我们想找到到达终端状态的最短路径。我们要最大化获得的奖励，因此目标状态s ∗ s ∗的奖励应高于其他状态的奖励。对于gridworld，我们将使用以下简单函数：

​

 评估

策略评估算法的目标   是评估策略π（s，a）π（s，a），即根据V（s）∀sV（s）∀s确定所有状态的值。该算法基于Bellman方程：

​

对于迭代k + 1k + 1，该方程式通过以下公式得出状态ss的值：

• π（s，a）π（s，a）：在状态ss中选择动作aa的概率
• Pass'Pss'a：使用动作aa从状态ss过渡到状态s's'的概率
• Rass'Rss'a：使用动作aa从状态ss过渡到状态s's'时的预期奖励
• γγ：贴现率
• Vπk（s'）Vkπ（s'）：在给定策略ππ的情况下，步骤kk中状态s's'的值

为了更好地理解方程式，让我们在gridworld的上下文中逐一考虑：

• π（s，a）π（s，a）：由于我们处于确定性环境中，因此策略仅指定一个动作aa，其中π（s，a）=1π（s，a）= 1，而所有其他动作a'a'具有π（s，a'）=0π（s，a'）= 0。因此，乘以π（s，a）π（s，a）只会选择策略指定的操作。
• ∑s′∑s′：该和是所有状态s′s′的总和，可以从当前状态ss得到。在gridworld中，我们只需要考虑相邻像元和当前像元本身，即s'∈{x | adj（x，s）∨x= s}s'∈{x | adj（x，s）∨x= s }。
• Pass'Pss'a：这是通过动作aa从状态ss过渡到s's'的概率。
• Rass'Rss'a：这是通过aa从ss过渡到s's'的奖励。请注意，在gridworld中，奖励仅由下一个状态s's'确定。
• γγ：折现因子调节预期奖励的影响。
• Vk（s'）Vk（s'）：在提议状态s's'的预期奖励。该术语的存在是政策评估是动态编程的原因：我们正在使用先前计算的值来更新当前值。

我们将使用γ=1γ= 1，因为我们处在一个情景 中，在达到目标状态时学习 停止。因此，值函数表示到达目标单元格的最短路径的长度。更准确地说，让d（s，s ∗）d（s，s ∗）表示从状态ss到目标的最短路径。然后，对于s≠s ∗ s≠s ∗，Vπ（s）=-d（s，s ∗）+1Vπ（s）=-d（s，s ∗）+ 1。

为了实施策略评估，我们通常将对状态空间进行多次扫描。每次扫描都需要前一次迭代中的值函数。新值和旧值函数之间的差异通常用作算法的终止条件：

def findConvergedCells(self, V_old, V_new, theta = 0.01):
    diff = abs(V_old-V_new)
    return np.where(diff < theta)[0]

该函数确定值函数差异小于θθ的网格单元的索引。当所有状态的值都收敛到稳定值时，我们可以停止。由于情况并非总是如此（例如，如果策略指定状态的动作不会导致目标，或者过渡概率/奖励配置不当），我们还要指定最大迭代次数。

达到停止条件后，  evaluatePolicy 返回最新的状态值函数：

def evaluatePolicy(self, gridWorld, gamma = 1):
    if len(self.policy) != len(gridWorld.getCells()):
        # sanity check whether policy matches dimension of gridWorld
        raise Exception("Policy dimension doesn't fit gridworld dimension.")
    maxIterations = 500
    V_old = None
    V_new = initValues(gridWorld) # sets value of 0 for viable cells
    iter = 0
    convergedCellIndices = np.zeros(0)
    while len(ConvergedCellIndices) != len(V_new):
        V_old = V_new
        iter += 1
        V_new = self.evaluatePolicySweep(gridWorld, V_old, gamma, convergedCellIndices)
        convergedCellIndices = self.findConvergedCells(V_old, V_new)
        if iter > maxIterations:
            break
    print("Policy evaluation converged after iteration: " + str(iter))
    return V_new

该evaluatePolicySweep 功能执行一次策略评估扫描  。该函数遍历网格中的所有单元并确定状态的新值.

请注意，该  ignoreCellIndices 参数表示后续扫描未更改值函数的像元索引。这些单元在进一步的迭代中将被忽略以提高性能。这对于我们的gridworld示例来说很好，因为我们只是想找到最短的路径。因此，状态值函数第一次不变时，这是其最佳值。

使用该evaluatePolicyForState 函数计算状态值  。该函数的核心实现了我们先前讨论的Bellman方程。此函数的重要思想是，在计算状态ss的值函数时，我们不想扫描所有状态s's'。这就是为什么  状态生成器  仅生成可能实际发生的状态（即，转换概率大于零）的原因。

 评估结果

有了适当的实现后，我们可以通过执行以下命令找到策略的状态值函数.

为了将值函数与策略一起绘制，我们可以在将用于表示地图的一维数组转换为二维数组后，使用matplotlib中的pyplot：

def drawValueFunction(V, gridWorld, policy):
    fig, ax = plt.subplots()
    im = ax.imshow(np.reshape(V, (-1, gridWorld.getWidth())))
    for cell in gridWorld.getCells():
        p = cell.getCoords()
        i = cell.getIndex()
        if not cell.isGoal():
            text = ax.text(p[1], p[0], str(policy[i]),
                       ha="center", va="center", color="w")
        if cell.isGoal():
            text = ax.text(p[1], p[0], "X",
                       ha="center", va="center", color="w")
    plt.show()

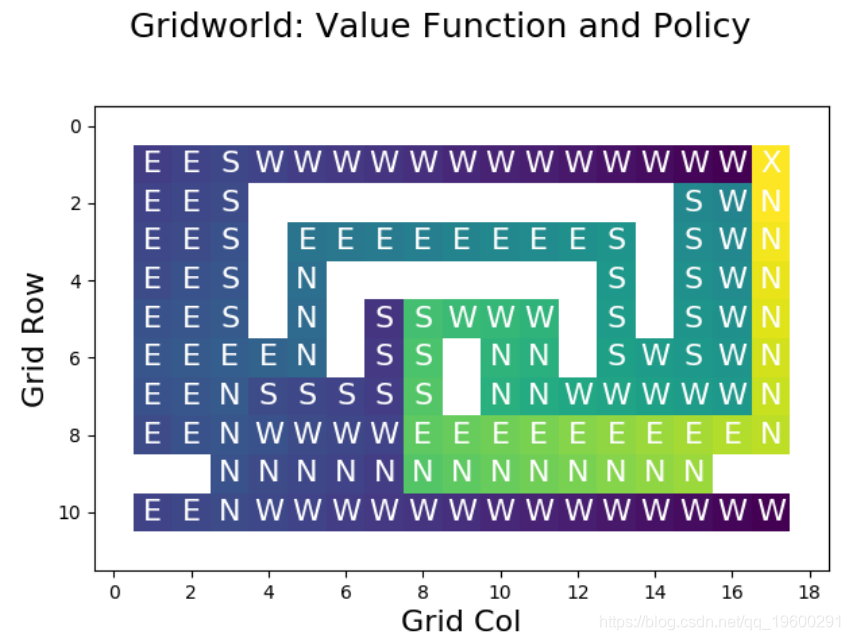
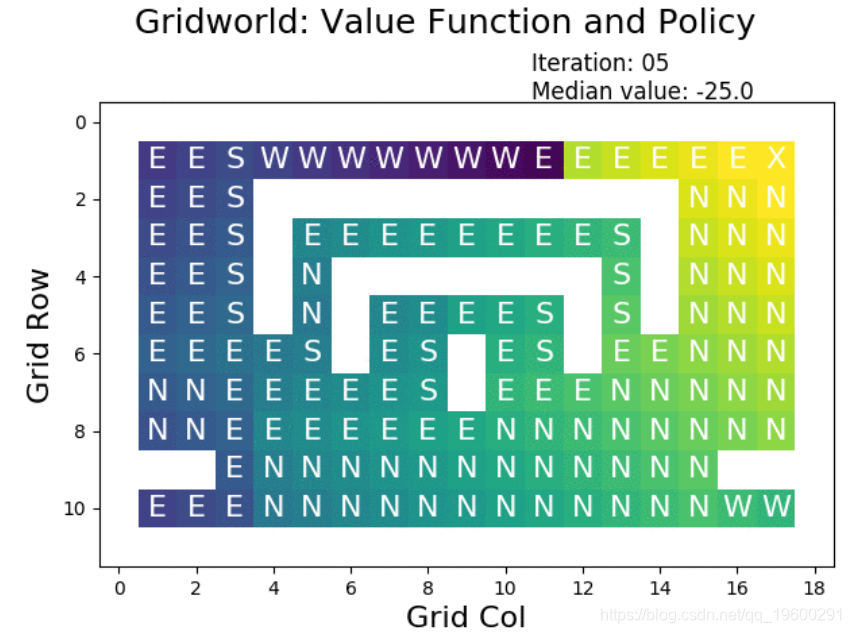
使用该函数，我们可以可视化策略的状态值函数：

​

对于非目标单元，将使用策略指定的操作对图进行注释。X 标签上方表示右上方单元格中的目标  。 

其他单元格的值由颜色指示。最差的状态（具有最低的奖励）以紫色显示，坏的状态以蓝色显示，蓝绿色的中间状态以绿色显示，良好的状态以绿色显示，非常好的状态（具有最高的奖励）显示为黄色。

查看这些值，我们可以看到结果与策略规定的操作相匹配。例如，直接位于目标西侧的状态的值非常低，因为该状态的动作（GO_WEST）会导致较长的弯路。位于目标正南方的单元格具有很高的价值，因为其作用（GO_NORTH）直接导致目标。

请注意，在以后的工作中，的性能  evaluatePolicy 至关重要，因为我们会多次调用它。对于计算的示例，该函数需要进行61次迭代，这在我的笔记本电脑上大约转换了半秒钟。请注意，对于更接近最佳策略的策略，策略评估将需要较少的迭代，因为值将更快地传播。

能够确定状态值函数非常好-现在我们可以量化所提议策略的优点了。但是，我们尚未解决寻找最佳政策的问题。这就是策略迭代起作用的地方。

策略迭代

现在我们已经能够计算状态值函数，我们应该能够  改进现有的策略。一种简单的策略是贪婪算法，该算法遍历网格中的所有单元格，然后根据值函数选择使预期奖励最大化的操作。

 其定义为

​

 improvePolicy 函数确定策略的值函数 ，然后调用  findGreedyPolicy 以标识每种状态的最佳操作.

要做的  findGreedyPolicy 是考虑每个单元并选择使预期奖励最大化的动作，从而构造输入策略的改进版本。例如，执行  improvePolicy 一次并重新评估策略后，我们得到以下结果：

​

与原始值函数相比，目标旁边的所有单元格现在都给了我们很高的回报，因为操作已得到优化。但是，我们可以看到这些改进仅仅是局部的。那么，我们如何获得最优政策呢？

策略迭代算法的思想   是，我们可以通过 迭代评估新策略的状态值函数来找到最优策略，并使用贪心算法对该策略进行改进，直到达到最优：

def policyIteration(policy, gridWorld):
    lastPolicy = copy.deepcopy(policy)
    lastPolicy.resetValues() # reset values to force re-evaluation of policy
    improvedPolicy = None
    while True:
        improvedPolicy = improvePolicy(lastPolicy, gridWorld)
        if improvedPolicy == lastPolicy:
            break
        improvedPolicy.resetValues() # to force re-evaluation of values on next run
        lastPolicy = improvedPolicy
    return(improvedPolicy)

策略迭代的结果

在gridworld上运行该算法可以在20次迭代中找到最佳解决方案-在我的笔记本上大约需要4.5秒。20次迭代后的终止并不令人惊讶：gridworld贴图的宽度为19。因此，我们需要进行19次迭代才能优化水平走廊的值。然后，我们需要进行一次额外的迭代来确定该算法可以终止，因为该策略未更​​改。

理解策略迭代的一个很好的工具是可视化每个迭代：

​

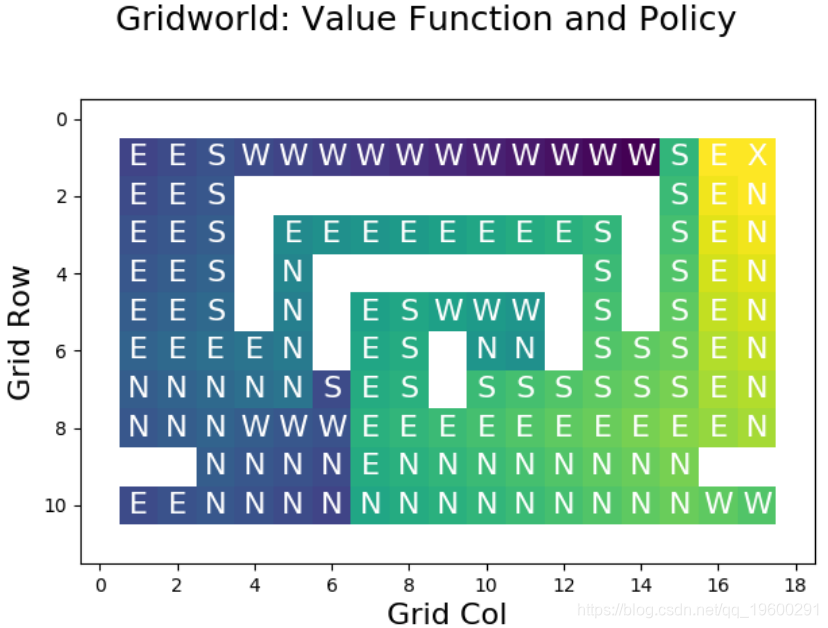
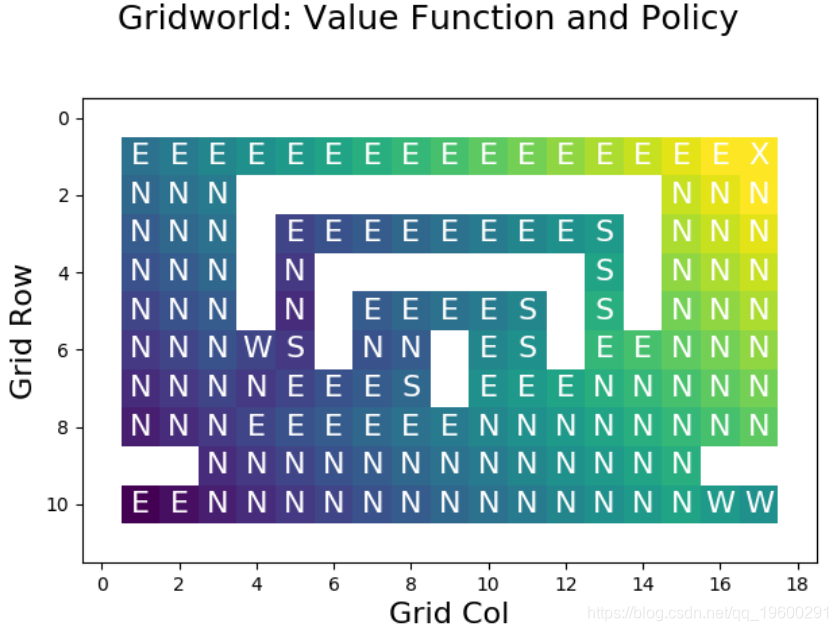
下图显示了使用策略迭代构造的最优值函数：

​

目视检查表明值函数正确，因为它为网格中的每个单元格选择了最短路径。

价值迭代

借助我们迄今为止探索的工具，出现了一个新问题：为什么我们根本需要考虑初始策略？价值迭代算法的思想   是我们可以在没有策略的情况下计算价值函数。与其让政策ππ指示选择了哪些操作，我们不选择那些使预期奖励最大化的操作：

​

因为价值迭代的计算与策略评估非常相似，所以我已经实现了将价值迭代evaluatePolicyForState 用于我先前定义的方法中的功能  。 

只要没有可用的策略，此函数就会执行值迭代算法。在这种情况下，  len(self.policy) 将为零，从而  pi 始终返回一个值，并且  V 被确定为所有动作的预期奖励的最大值。

因此，要实现值迭代，我们不必做很多编码。我们只需要evaluatePolicySweep 在Policy 对象的值函数未知的情况下迭代调用该  函数，  直到该过程为我们提供最佳结果为止。然后，要确定相应的策略，我们只需调用findGreedyPolicy 我们先前定义的  函数.

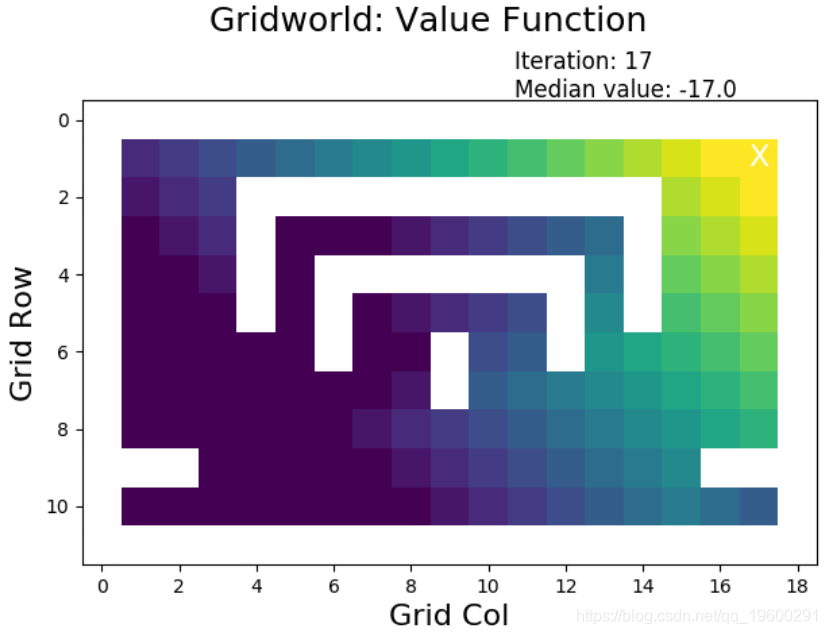
价值迭代的结果

当执行值迭代时，奖励（高：黄色，低：黑暗）从目标的最终状态（右上方  X）扩展到其他状态：

​

摘要

我们已经看到了如何在MDP中应用强化学习。我们的工作假设是我们对环境有全面的了解，并且代理完全了解环境。基于此，我们能够促进动态编程来解决三个问题。首先，我们使用策略评估来确定给定策略的状态值函数。接下来，我们应用策略迭代算法来优化现有策略。第三，我们应用价值迭代从头开始寻找最佳策略。