了解浮点数的编码形式
1. 整数的编码
先看下整数在计算机中的编码方式。
在计算机中,无符号数编码只能表示非负数,有符号数能表示负数、零和正数。常见的有符号数使用补码形式进行编码。补码编码中最高位表示负权,0表示正数,1则表示为负数。
对于一个正整数的二进制串(以8bit为例):00010000,它表示的十进制值为16(2^4);如果是负数的话,负整数的二进制串11110000,它对应的十进制数为-16。
运算过程:
11110000 --->
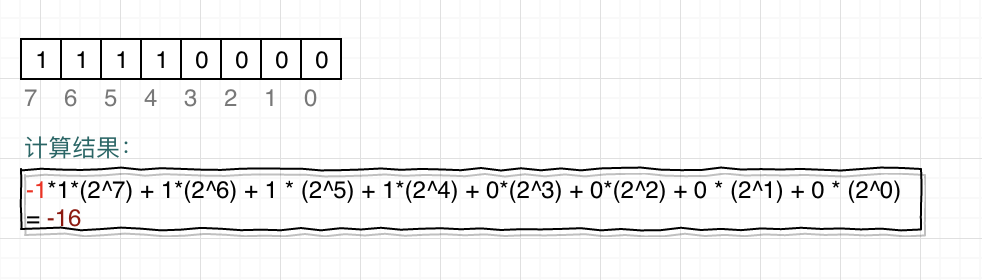
2. 浮点数的编码
通常十进制数1234可以表示成123.4 x 10、12.34 x 10^2、1.234 x 10^3、0.1234 x 10^4 ...,十进制中基数是10。那么对应到二进制数中时,其基数是2,一个二进制数(8bit为例) 11111111也可以表示成1111111.1 x 2 、111111.11 x 2^2、11111.111 x 2^3、1.1111111 x 2^7... 对于一个二进制小数1.1101要将它转成十进制数,也是每一位乘上该位的位权1*2 + 1*(2^-1) + 1*(2^-2) + 0*(2^-3) + 1*(2^-4)
浮点数使用(-1)^s x M x 2^E表示,其中由四部分组成:
- s-符号标志位
- M是小数部分称作
- 2位
- E则是指数部分称作
IEEE浮点数中将这三部分符号、尾数、阶码组装在一起形成了浮点数的编码格式。
- 占用4B即32位,符号位占用,阶码部分由组成,剩下表示小数部分。
- 占用8B即64位,符号位占用,阶码部分由组成,剩下表示小数部分。
下图表示两种不同精度浮点数的编码格式,
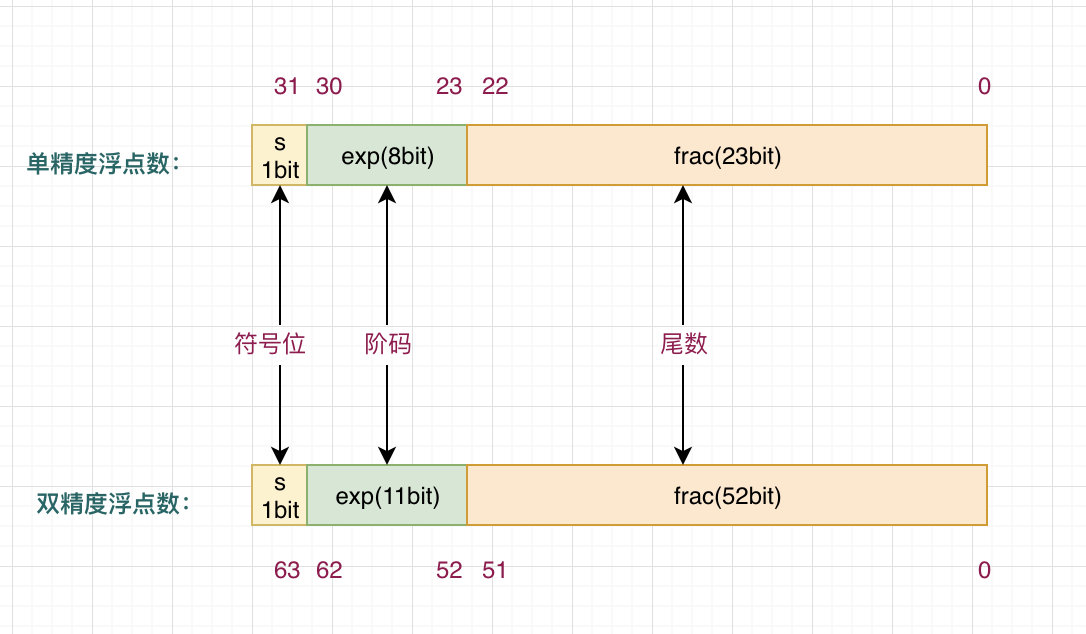
下面基于单精度浮点数编码格式阶码和尾数部分进行详述。了解了单精度,双精度就同样了解了。
-
:阶码部分8位,能表示的值范围为0~255,但通常指数部分可以有小数,用这8位来表示有符号整数时,引入一个偏置值(bias)。如果阶码部分用k位表示,则偏置值为
2^(k-1) - 1也就是01111111...,实际阶码部分表示的值换算成指数值时需要减去这个偏置值。对于阶码位00000001,它对应的指数值为(1 - 127 = -126)。
*a. 对于阶码中全0时,它表示的指数值为
(1-偏置值),单精度中就为-126,通常用来表示0或非常接近0的小数。0的编码格式为0 00000000 00000000000000000000000*b. 阶码全1时,又分成两种情况:
i. 尾数部分全0,则该值表示为无穷大(前面的符号位表示是正无穷大还是负无穷大)ii. 尾数部分不全为0,则该值表示NaN(Not a Number)
所以阶码部分表示的值范围为-126 ~ 127
- :对于前面阶码不是特殊值时(全0或全1),尾数部分表示的二进制小数值为
1 + 0.尾数部分
如果阶码为全0时,尾数部分表示的二进制值为0.尾数部分
来看个简单的例子,就可以更好的理解上面的描述:

3. JAVA中查看浮点数的编码形式
java中查看一个数的浮点数的二进制表示形式:
public static void main(String[] args) {
float f = 3510593.0f;
String binaryStr = Integer.toBinaryString(Float.floatToIntBits(f));
String hexStr = Integer.toHexString(Float.floatToIntBits(f));
System.err.println(String.format("float number:%s
binary format: %s
hex foramt:0x%s", f, binaryStr, hexStr));
}
输出结果:
float number:3510593.0
binary format: 1001010010101100100010100000100
hex foramt:0x4a564504
【参考】[深入理解计算机系统] 第三版
作者:sv
出处:https://www.cnblogs.com/sv00
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。