优先队列BFS:
这个八数码问题本身其实是之前人工智能实验课的作业……
首先,如果不带估价函数,直接用优先队列BFS,肯定也是能得到正确结果的,至于用时怎么样,可以看评测结果……
代码:
#include<bits/stdc++.h> using namespace std; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; string ed="123804765"; struct Node { int dist; int x,y; string mp; #define X(idx) (idx/3) #define Y(idx) (idx%3) char& val(int i,int j){return mp[i*3+j];} void Zero() { for(int i=0;i<9;i++) { if(mp[i]!='0') continue; x=X(i), y=Y(i); break; } } bool operator<(const Node& o)const{return dist>o.dist;} }st; map<string,bool> vis; priority_queue<Node> Q; int main() { cin>>st.mp; st.dist=0; st.Zero(); vis.clear(); Q.push(st), vis[st.mp]=1; while(Q.size()) { Node now=Q.top(); Q.pop(); if(now.mp==ed) { cout<<now.dist<<endl; break; } for(int k=0;k<4;k++) { Node nxt=now; nxt.x+=dx[k], nxt.y+=dy[k], nxt.dist++; if(nxt.x<0 || nxt.x>2 || nxt.y<0 || nxt.y>2) continue; swap(nxt.val(now.x,now.y),nxt.val(nxt.x,nxt.y)); if(!vis[nxt.mp]) Q.push(nxt), vis[nxt.mp]=1; } } }
评测结果:
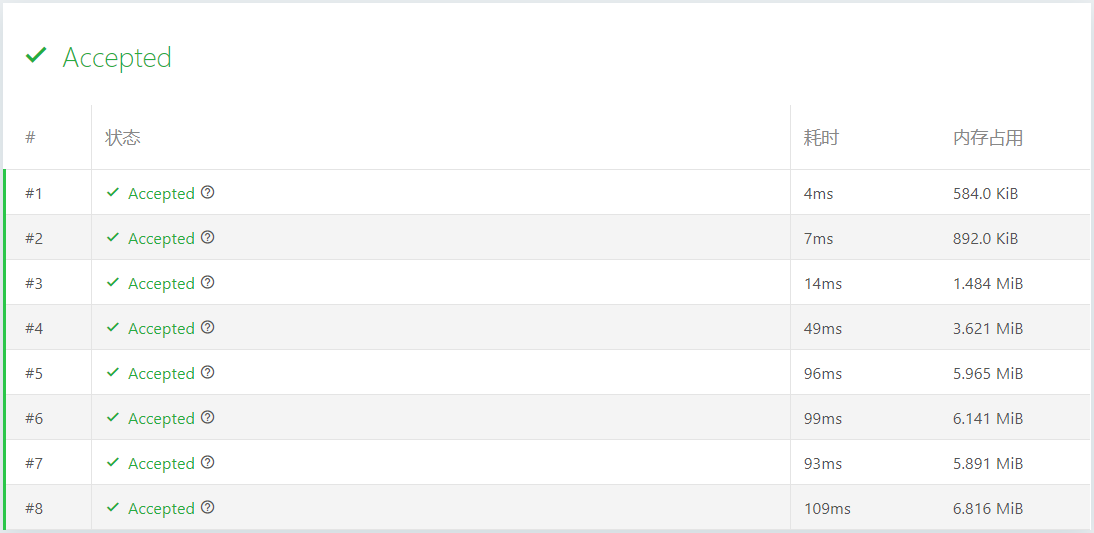
Astar算法:
然后,我们知道,优先队列BFS里的优先队列,是一个维护当前代价的二叉堆,
我们接下来增加Astar算法的估价函数 $eval(x)$,考虑到要这个估价函数,是要不大于从当前状态到目标状态的实际代价的,
因此我考虑将其设定成:将当前状态下的九宫格看做一个长度为 $9$ 的字符串 $s$,目标状态也可以看做一个字符串 $t = "123804765"$,统计这两个字符串使得 $s_i eq t_i$ 的 $i$ 的个数,记为 $e$,再取 $eval(x) = lfloor frac{e}{2} floor$ 即可。
这也是很好理解的,因为不可能用更少的步数使得当前状态变为目标状态了。
AC代码:
#include<bits/stdc++.h> using namespace std; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; string ed="123804765"; struct Node { int dist,eval; int x,y; string mp; #define X(idx) (idx/3) #define Y(idx) (idx%3) char& val(int i,int j){return mp[i*3+j];} void Zero() { for(int i=0;i<9;i++) { if(mp[i]!='0') continue; x=X(i), y=Y(i); break; } } void Eval() { eval=0; for(int i=0;i<9;i++) eval+=(mp[i]!=ed[i]); eval/=2; } bool operator<(const Node& o)const { return dist+eval>o.dist+o.eval; } }st; map<string,bool> vis; priority_queue<Node> Q; int main() { cin>>st.mp; st.dist=0; st.Zero(); st.Eval(); vis.clear(); Q.push(st), vis[st.mp]=1; while(Q.size()) { Node now=Q.top(); Q.pop(); if(now.mp==ed) { cout<<now.dist<<endl; break; } for(int k=0;k<4;k++) { Node nxt=now; nxt.x+=dx[k], nxt.y+=dy[k], nxt.dist++; if(nxt.x<0 || nxt.x>2 || nxt.y<0 || nxt.y>2) continue; swap(nxt.val(now.x,now.y),nxt.val(nxt.x,nxt.y)); if(!vis[nxt.mp]) { nxt.Eval(); Q.push(nxt), vis[nxt.mp]=1; } } } }
评测结果:
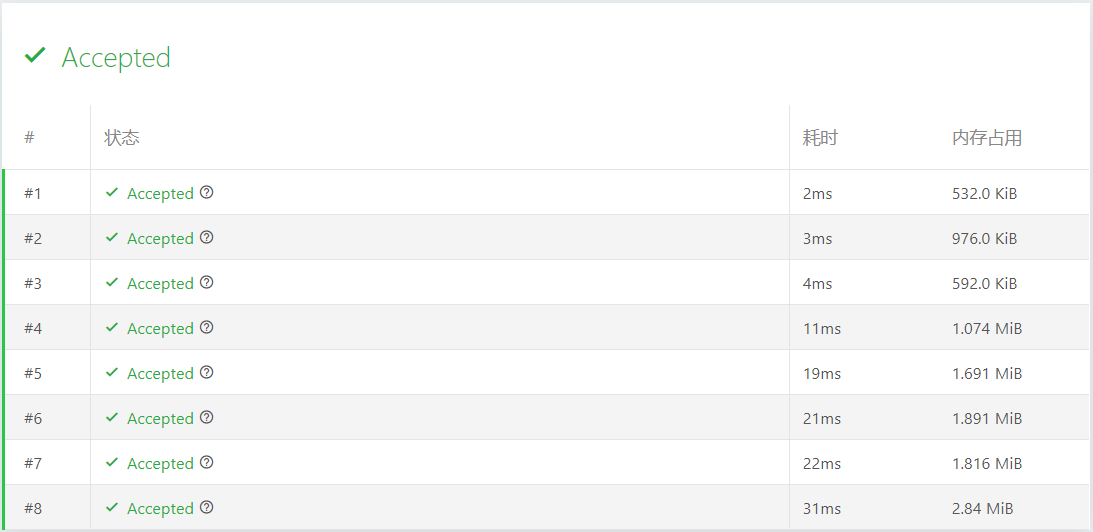
总结:
比较普通的优先队列维护下的BFS,和加了估价算法的Astar算法,可以明显看到时间和空间的使用都明显降低了。
(鉴于有可能会有同样在做这个实验的同学搜索到本文,我还是要声明一下:上面的两个代码都是我亲手敲的,没有看网上任何别的博客,想要拿去借鉴的同学,建议看懂了之后根据自己的思路做一些修改乃至优化……直接抄袭这样的事情最好还是不要做……)