SAS学习 day5

多因素方差分析

方差分析

1. 比较总体均值的差异性
2. 比较多总体多重比较下两两个体间的差异 通过lsmeans
3. 也还可以作为预测模型 

只有主效应： Xij = u + ai + Bj +eij

有交互效应：Xij = u + ai + Bj + (aB)ij + eij

无交互效应：随着药物剂量水平的增加，不论疾病a或b，其血压都随之升高

有交互效应：随着药物剂量水平增加，疾病a血压升高；疾病b血压降低

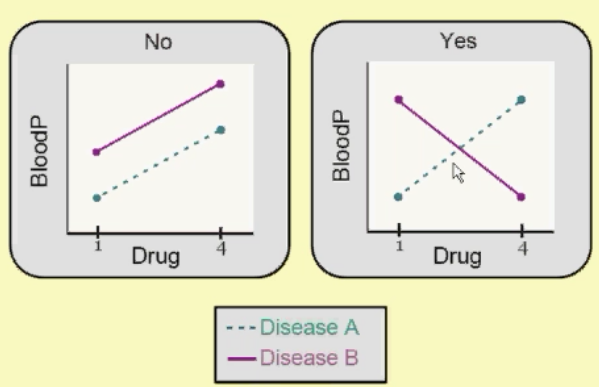
无交互效应的一个例子：

proc glm data = ol.b_roads1;
class paint road;
model bright = paint road;  选定两个变量 但认为他们相互独立
lsmeans paint / pdiff =all adjust =tukey; 用tukey来进行比较
title 'paint data: 多重比较包括道路';
run;

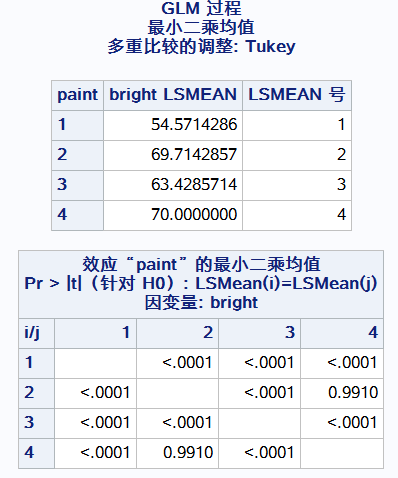
第2和第4差异性不大

 总的结论在paint和road两个因素影响下，总体均值有差异

 有交互效应     gplot过程

proc gplot data = ol.b_drug;
symbol c =blue w=2 interpol = stdlmtj line=1;
symbol2 c=green w=2 interpol = stdlmtj line=2;
symbol3 c=red w=2 interpol = stdlmtj line=3;  可要可不要  标记颜色
plot bloodp*drug = disease;    *左边bloodp即为y  *的右边x1 x2
title" 证明疾病和药物之间的关系";
run;

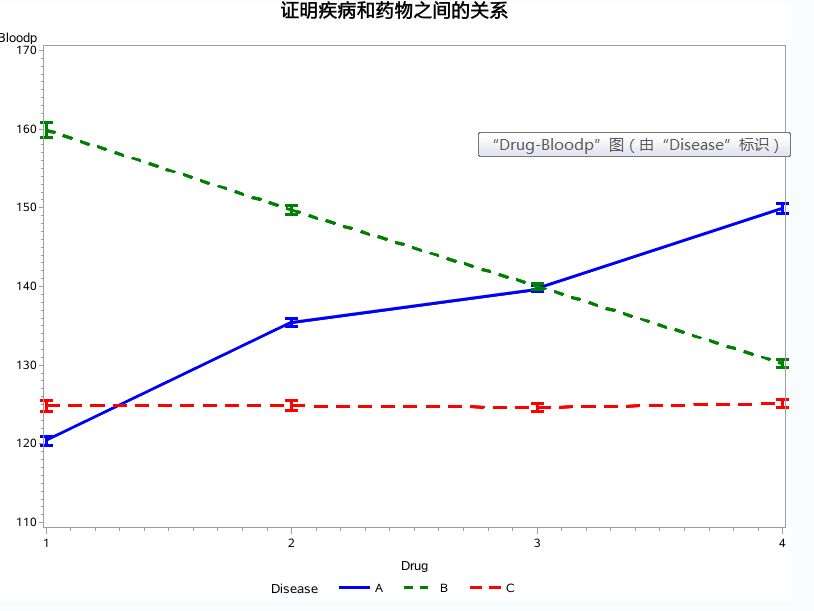
 可以看出药物1,2,3,4，在疾病a，b，c上都有交互关系  特别是b和a交互效应明显

 先用gplot图测一下 线条有交叉可以肯定有交互效应

proc glm data = ol.b_drug;
class disease drug;
model bloodp = disease drug disease*drug;三个变量  可以用@2代替disease*drug  要确定不同变量间都有相关关系 才可以用@这种语法

title "有交互效应"; run;

 

从p值可以看出交互效应有影响

 lsmeans不加可以鉴别总体均值水平的差异 也可以鉴别样本中均值水平的差异