题目:
有N堆石子,现要将石子有序的合并成一堆,规定如下:
1.每次只能移动相邻的2堆石子合并
2.合并花费为新合成的一堆石子的数量。
求将这N堆石子合并成一堆的总花费最小(或最大)。
样例:
输入:7
13 7 8 16 21 4 18
输出:239
说是简单dp,刚开始学dp还是有点困难,这个题目我花了很长时间了。今天差不多才理清里面的大部分细节。
首先,合并相邻的石子,合并时,可以两堆,三堆,四堆。两堆的时候就只能合并相邻两堆;三堆的时候就有多种选择了,1+2 和 2+1;四堆的时候,1+3 和 2+2 和 3+1;
2堆的时候:
3堆的时候:
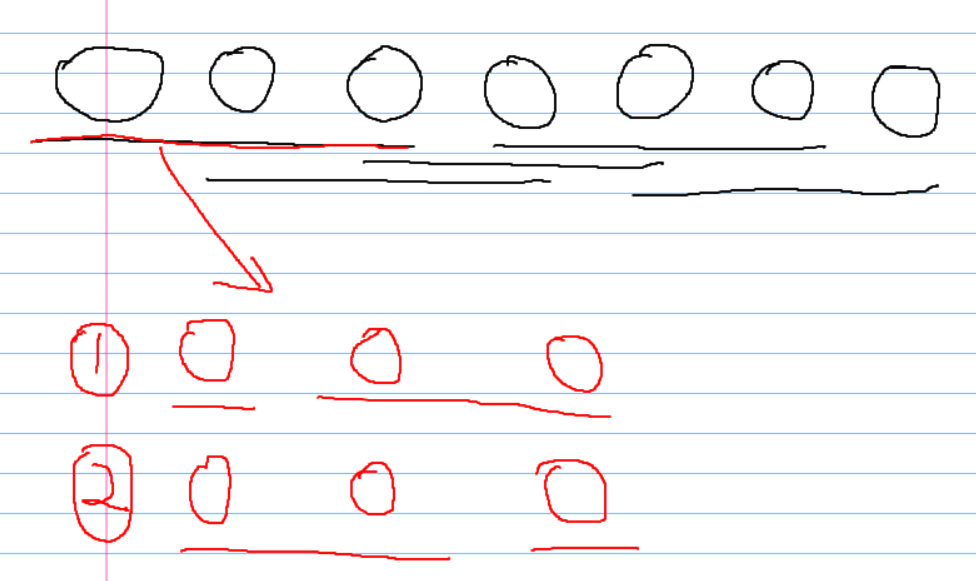
4堆也是类似。
现在我们拿样例来分析一下。
1.首先是状态转移方程。
设f[i][j]是从第i堆到第j堆的最优值。 配和上面的图,两堆的时候:f[1][2] f[2][3] f[3][4] f[4][5] f[5][6] f[6][7]; 三堆的时候:f[1][3] f[2][4] ......。
然后 f[1][3] = f[1][1] + f[2][3] + s[3] - s[0]; f[1][3] = f[1][2] + f[3][3] + s[3] - s[0]; 有这两种情况。取他们的最小值。
转移方程就是 f[i][j] = min( f[i][j], f[i][k] + f[k+1][j] +s[j]-s[i]);
2.为什么是s[3] - s[0]呢?
s[3] - s[0]是从第1堆到第3堆的总和。但是花销并不仅仅是总和, 合并3堆的时候,其实是需要合并两次,所以每堆都用到了两次,而自己和自己合并,花费的价值为0。f[1][3] = f[1][1] + f[2][3] + s[3] - s[0]; f[1][1] + f[2][3]这个是一次合并,s[3] - s[0]这个是另外一次合并。
3.输出的答案是f[1][n]。
代表从第1堆到第n堆的最小花费。
4.为什么要倒推?
因为顺推的时候,f[1][3] = f[2][3] + f[1][1] ,顺推的话,i从1开始,那f[2][3]这个时候是没办法知道的。所以倒推。
代码:
#include<bits/stdc++.h>
using namespace std;
const int M = 10009;
int f[M][M]; // f[i][j] 代表第 i 堆石子 到 第 j 堆石子的最优值
int x,s[M];
int main(){
int n;
cin>>n;
memset(f,1011/3,sizeof(f));
for(int i = 1; i <= n; i++)
{
cin>>x;
s[i] = s[i-1] + x; //s[i] 代表前 i 堆石子的总和
}
for(int i = 1; i <= n; i++) f[i][i] = 0;
for(int i = n-1; i >= 1; i--)
for(int j = i+1; j <= n; j++)
for(int k = i; k <= j-1; k++)
{
f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
}
cout<<f[1][n];
return 0;
}