【CF117C】Cycle

题目

题目链接：https://codeforces.com/contest/117/problem/C
给定一张竞赛图，求任意一个大小为 (3) 的环。
(nleq 5000)。

思路

给出一种非常简洁的做法。
考虑对于一个点 (x)，我们能找到两个点 (y,z)，满足它们之间的连边如下：

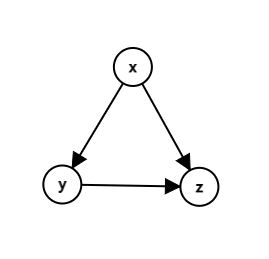
那么 (x o z) 这条边一定是没用的，也就是如果我们能找到一个大小为 (3) 的环包含 (x o z) 这条边，那么我们一定可以找出另一个不包含 (x o z) 这条边的大小为 (3) 的环。如下图

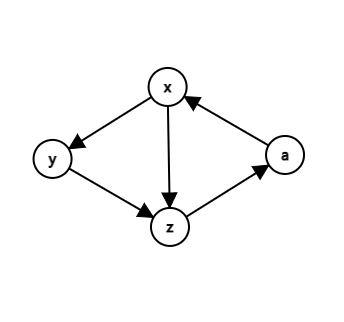
假设 (z,a,x) 三个点形成了一个大小为 (3) 的环，那么考虑 (a) 和 (y) 之间的连边，如果是 (a o y)，那么 (a,y,z) 三个点可以形成另一个环；如果是 (y o a)，那么 (a,x,y) 三个点可以形成另一个环。
所以我们可以直接把 (x o z) 这条边忽略掉。
这样的话把若干条边忽略后，每一个点最多只有一条出边。那么我们只需要枚举两个点 (i,j)，再判断 (i, ext{to}_i,j) 三点是否形成环即可。
时间复杂度 (O(n^2))，代码仅有 459B。

代码

#include <bits/stdc++.h>
using namespace std;

const int N=5010;
int n,to[N];
char a[N][N];

int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		scanf("%s",a[i]+1);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			if (a[i][j]==49 && (!to[i] || a[j][to[i]]==49)) to[i]=j;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			if (a[to[i]][j]==49 && a[j][i]==49)
				return printf("%d %d %d
",i,to[i],j),0;
	printf("-1");
	return 0;
}