k-d tree算法

转：https://www.cnblogs.com/eyeszjwang/articles/2429382.html

k-d树（k-dimensional树的简称）核心: 构建索引树，快速查找

下面是6个二维数据点{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}的k-d树空间划分示意图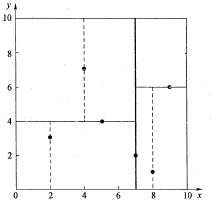

 

二维数据k-d树空间划分示意图

算法主要有两步骤：

1. 确定split的dimension：统计数据点每个dimension上的数据方差，选取方差最大的哪个dimension
2. 确定数据分割点：当前数据点集按其第split的那个dimension排序。位于正中间的那个数据点被选为Node-data，作为分割点
3. 重复上述两个步骤，知道当前数据点集为空。

 

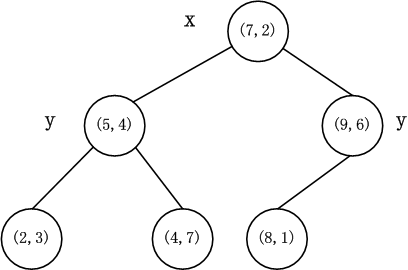
上述实例生成的k-d树

 

PS：每一级节点旁边的'x'和'y'表示以该节点分割左右子空间时split所取的dimension。

k-d树上的最邻近查找算法

关键：’回溯‘操作 -- 通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行'回溯'操作：算法沿搜索路径反向查找是否有距离查询点更近的数据点

一个复杂点的例子如查找点为（2，4.5）。先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<（7,2），（5,4），（4,7）>，取（4,7）为当前最近邻点，计算其与目标查找点的距离为3.202。然后回溯到（5,4），计算其与查找点之间的距离为3.041。以（2，4.5）为圆心，以3.041为半径作圆，如图5所示。可见该圆和y = 4超平面交割，所以需要进入（5,4）左子空间进行查找。此时需将（2,3）节点加入搜索路径中得<（7,2），（2,3）>。回溯至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2，3），最近距离更新为1.5。回溯至（7,2），以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割，如图6所示。至此，搜索路径回溯完。返回最近邻点（2,3），最近距离1.5。k-d树查询算法的伪代码如表3所示。

 

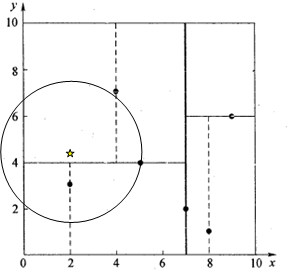
查找（2，4.5）点的第一次回溯判断

查找（2，4.5）点的第二次回溯判断