浮点数可以进行比较,但是浮点数由于表示精度在不同浮点数类型中的差异,所以会被误用。例如:
1 #include <iostream> 2 using namespace std; 3 4 int main() 5 { 6 float f1 = 7.123456789; 7 float f2 = 7.132456875; 8 cout << (f1 != f2 ? "not same " : "same "); 9 10 float g = 1.0 / 3.0; 11 double d = 1.0 / 3.0; 12 cout << (g==d ? "same " : "not same "); 13 14 system("pause"); 15 return 0; 16 }

当你满怀信心读完程序后,想象出的运行结果却与真实的运行结果不同的时候,你会如何想?
首先,由于十进制单精度浮点数的有效位数为7,两个前7位相等而后面不同的数有可能在计算机中表示为同一个浮点数,因而判断两数不等而失败!
为了避免这类问题,请统一使用double,而不要混用不同精度的浮点。对于C++来说,float已是昔日黄花,除了过渡一些C程序,在新编的程序中实在没有太大用处,因为double完全包含了它,而且浮点运算在内部都是先化为double进行的,使用float还必须付出转换回来的时间开销,因此混进float只会添乱!!
另外,由于浮点数在计算机内实际上是一个近似表示,在手工计算看来为正确的结果,在计算机中运算未必能得出正确的结果。例如:
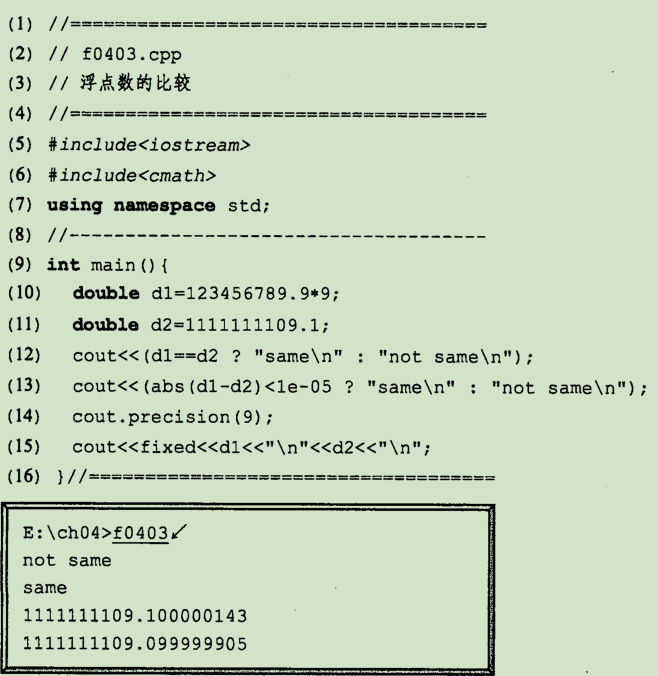
因为浮点数的构成原理,决定了十进制数在转换为内部浮点数时,由无穷尾数而带来的不精确性。上面程序中d1和d2变量的值本应相等,却在计算机内部为不等。
所以,我们还得到另外一个重要的经验:使用浮点数进行相等(==)和不等(!=)比较的操作通常是有问题的。浮点数的相等比较,一般总是使用两者相减的值是否落在0的邻域中来判断的。上面程序中第13行语句所示的邻域比较技术,请多多体会,进而模仿!