02-机器学习_第2天(kmeans聚类算法与应用)
机器学习算法day02_Kmeans聚类算法及应用
课程大纲
|
Kmeans聚类算法原理 |
Kmeans聚类算法概述 |
|
Kmeans聚类算法图示 |
|
|
Kmeans聚类算法要点 |
|
|
Kmeans聚类算法案例 |
需求 |
|
用Numpy手动实现 |
|
|
用Scikili机器学习算法库实现 |
|
|
Kmeans聚类算法补充 |
算法缺点 |
|
改良思路 |
课程目标:
1、理解Kmeans聚类算法的核心思想
2、理解Kmeans聚类算法的代码实现
3、掌握Kmeans聚类算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. Kmeans聚类算法原理
1.1 概述
K-means算法是集简单和经典于一身的基于距离的聚类算法
采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。
该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
1.2 算法图示
假设我们的n个样本点分布在图中所示的二维空间。
从数据点的大致形状可以看出它们大致聚为三个cluster,其中两个紧凑一些,剩下那个松散一些,如图所示:
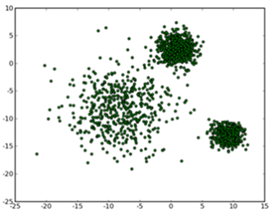
我们的目的是为这些数据分组,以便能区分出属于不同的簇的数据,给它们标上不同的颜色,如图:

1.3 算法要点
1.3.1 核心思想
通过迭代寻找k个类簇的一种划分方案,使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
k-means算法的基础是最小误差平方和准则,
其代价函数是:
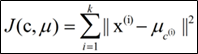
式中,μc(i)表示第i个聚类的均值。
各类簇内的样本越相似,其与该类均值间的误差平方越小,对所有类所得到的误差平方求和,即可验证分为k类时,各聚类是否是最优的。
上式的代价函数无法用解析的方法最小化,只能有迭代的方法。
1.3.2 算法步骤图解
下图展示了对n个样本点进行K-means聚类的效果,这里k取2。
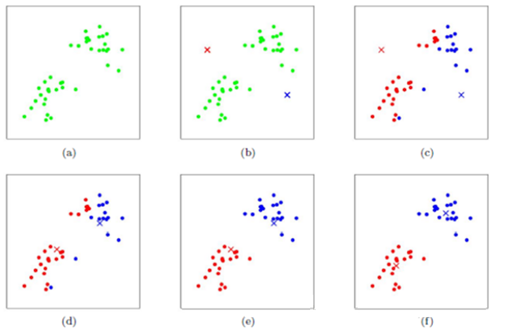
1.3.3 算法实现步骤
k-means算法是将样本聚类成 k个簇(cluster),其中k是用户给定的,其求解过程非常直观简单,具体算法描述如下:
1) 随机选取 k个聚类质心点
2) 重复下面过程直到收敛 {
对于每一个样例 i,计算其应该属于的类:

对于每一个类 j,重新计算该类的质心:

}
其伪代码如下:
********************************************************************
创建k个点作为初始的质心点(随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每一个数据点
对每一个质心
计算质心与数据点的距离
将数据点分配到距离最近的簇
对每一个簇,计算簇中所有点的均值,并将均值作为质心
2. Kmeans分类算法Python实战
2.1 需求
对给定的数据集进行聚类
本案例采用二维数据集,共80个样本,有4个类。样例如下:
testSet.txt
|
1.658985 4.285136 -3.453687 3.424321 4.838138 -1.151539 -5.379713 -3.362104 0.972564 2.924086 -3.567919 1.531611 0.450614 -3.302219 -3.487105 -1.724432 2.668759 1.594842 -3.156485 3.191137 3.165506 -3.999838 -2.786837 -3.099354 4.208187 2.984927 -2.123337 2.943366 0.704199 -0.479481 -0.392370 -3.963704 2.831667 1.574018 -0.790153 3.343144 2.943496 -3.357075 |
2.2 python代码实现
2.2.1 利用numpy手动实现
|
from numpy import * #加载数据 def loadDataSet(fileName): dataMat = [] fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split(' ') fltLine = map(float, curLine) #变成float类型 dataMat.append(fltLine) return dataMat # 计算欧几里得距离 def distEclud(vecA, vecB): return sqrt(sum(power(vecA - vecB, 2))) #构建聚簇中心,取k个(此例中为4)随机质心 def randCent(dataSet, k): n = shape(dataSet)[1] centroids = mat(zeros((k,n))) #每个质心有n个坐标值,总共要k个质心 for j in range(n): minJ = min(dataSet[:,j]) maxJ = max(dataSet[:,j]) rangeJ = float(maxJ - minJ) centroids[:,j] = minJ + rangeJ * random.rand(k, 1) return centroids #k-means 聚类算法 def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent): m = shape(dataSet)[0] clusterAssment = mat(zeros((m,2))) #用于存放该样本属于哪类及质心距离 centroids = createCent(dataSet, k) clusterChanged = True while clusterChanged: clusterChanged = False; for i in range(m): minDist = inf; minIndex = -1; for j in range(k): distJI = distMeans(centroids[j,:], dataSet[i,:]) if distJI < minDist: minDist = distJI; minIndex = j if clusterAssment[i,0] != minIndex: clusterChanged = True; clusterAssment[i,:] = minIndex,minDist**2 print centroids for cent in range(k): ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 去第一列等于cent的所有列 centroids[cent,:] = mean(ptsInClust, axis = 0) return centroids, clusterAssment |
2.2.2 利用scikili库实现
Scikit-Learn是基于python的机器学习模块,基于BSD开源许可证。
scikit-learn的基本功能主要被分为六个部分,分类,回归,聚类,数据降维,模型选择,数据预处理。包括SVM,决策树,GBDT,KNN,KMEANS等等
Kmeans在scikit包中即已有实现,只要将数据按照算法要求处理好,传入相应参数,即可直接调用其kmeans函数进行聚类
|
################################################# # kmeans: k-means cluster ################################################# from numpy import * import time import matplotlib.pyplot as plt ## step 1:加载数据 print "step 1: load data..." dataSet = [] fileIn = open('E:/Python/ml-data/kmeans/testSet.txt') for line in fileIn.readlines(): lineArr = line.strip().split(' ') dataSet.append([float(lineArr[0]), float(lineArr[1])]) ## step 2: 聚类 print "step 2: clustering..." dataSet = mat(dataSet) k = 4 centroids, clusterAssment = kmeans(dataSet, k) ## step 3:显示结果 print "step 3: show the result..." showCluster(dataSet, k, centroids, clusterAssment) |
2.2.3 运行结果
不同的类用不同的颜色来表示,其中的大菱形是对应类的均值质心点。

3、Kmeans算法补充
3.1 kmeans算法缺点
k-means算法比较简单,但也有几个比较大的缺点:
(1)k值的选择是用户指定的,不同的k得到的结果会有挺大的不同,如下图所示,左边是k=3的结果,这个就太稀疏了,蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果,可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的:

(2)对k个初始质心的选择比较敏感,容易陷入局部最小值。例如,我们上面的算法运行的时候,有可能会得到不同的结果,如下面这两种情况。K-means也是收敛了,只是收敛到了局部最小值:

(3)存在局限性,如下面这种非球状的数据分布就搞不定了:

(4)数据集比较大的时候,收敛会比较慢。
3.2 改良思路
k-means老早就出现在江湖了。所以以上的这些不足也已有了对应方法进行了某种程度上的改良。例如:
ü 问题(1)对k的选择可以先用一些算法分析数据的分布,如重心和密度等,然后选择合适的k
ü 问题(2),有人提出了另一个成为二分k均值(bisecting k-means)算法,它对初始的k个质心的选择就不太敏感
02-机器学习_第2天(knn分类算法与应用) - 简化版
机器学习算法day02_KNN分类算法及应用
课程大纲
|
KNN分类算法原理 |
KNN概述 |
|
KNN算法图示 |
|
|
KNN算法要点 |
|
|
KNN算法不足之处 |
|
|
KNN分类算法Python实战 |
KNN简单数据分类实践 |
|
KNN实现手写数字识别 |
|
|
KNN算法补充 |
KNN算法中k值的选取 |
|
类别判定 |
|
|
如何选择合适的衡量距离 |
|
|
训练样本/性能问题 |
课程目标:
1、理解KNN算法的核心思想
2、理解KNN算法的实现
3、掌握KNN算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. kNN分类算法原理
1.1 概述
K最近邻(k-Nearest Neighbor,KNN)分类算法是最简单的机器学习算法。[dht1]
KNN算法的指导思想是“近朱者赤,近墨者黑”,由你的邻居来推断出你的类别。
本质上,KNN算法就是用距离来衡量样本之间的相似度
1.2 算法图示
v 从训练集中找到和新数据最接近的k条记录,然后根据多数类来决定新数据类别。
v 算法涉及3个主要因素:
1) 训练数据集
2) 距离或相似度的计算衡量
3) k的大小

v 算法描述
1) 已知两类“先验”数据,分别是蓝方块和红三角,他们分布在一个二维空间中
2) 有一个未知类别的数据(绿点),需要判断它是属于“蓝方块”还是“红三角”类
3) 考察离绿点最近的3个(或k个)数据点的类别,占多数的类别即为绿点判定类别
1.3 算法要点
1.3.1、计算步骤
计算步骤如下:
1)算距离:给定测试对象,计算它与训练集中的每个对象的距离
2)找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻
3)做分类:根据这k个近邻归属的主要类别,来对测试对象分类
1.3.2、相似度的衡量
v 距离越近应该意味着这两个点属于一个分类的可能性越大。
但,距离不能代表一切,有些数据的相似度衡量并不适合用距离
v 相似度衡量方法:包括欧式距离、夹角余弦等。
(简单应用中,一般使用欧氏距离,但对于文本分类来说,使用余弦(cosine)来计算相似度就比欧式(Euclidean)距离更合适)
1.3.3、类别的判定
v 简单投票法:少数服从多数,近邻中哪个类别的点最多就分为该类。
v 加权投票法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大(权重为距离平方的倒数)
1.4 算法不足之处
- 样本不平衡容易导致结果错误
² 如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
² 改善方法:对此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
- 计算量较大
² 因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
² 改善方法:事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
该方法比较适用于样本容量比较大的类域的分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
2. KNN分类算法Python实战
2.1 kNN简单数据[dht2] 分类实践
2.1.1 需求
<比如:计算地理位置的相似度>
……
有以下先验数据,使用knn算法对未知类别数据分类
|
属性1 |
属性2 |
类别 |
|
1.0 |
0.9 |
A |
|
1.0 |
1.0 |
A |
|
0.1 |
0.2 |
B |
|
0.0 |
0.1 |
B |
未知类别数据
|
属性1 |
属性2 |
类别 |
|
1.2 |
1.0 |
? |
|
0.1 |
0.3 |
? |
2.1.2 Python实现
首先,我们新建一个kNN.py脚本文件,文件里面包含两个函数,一个用来生成小数据集,一个实现kNN分类算法。代码如下:
|
######################################### # kNN: k Nearest Neighbors # 输入: newInput: (1xN)的待分类向量 # dataSet: (NxM)的训练数据集 # labels: 训练数据集的类别标签向量 # k: 近邻数
# 输出: 可能性最大的分类标签 ######################################### from numpy import * import operator #创建一个数据集,包含2个类别共4个样本 def createDataSet(): # 生成一个矩阵,每行表示一个样本 group = array([[1.0, 0.9], [1.0, 1.0], [0.1, 0.2], [0.0, 0.1]]) # 4个样本分别所属的类别 labels = ['A', 'A', 'B', 'B'] return group, labels # KNN分类算法函数定义 def kNNClassify(newInput, dataSet, labels, k): numSamples = dataSet.shape[0] # shape[0]表示行数 ## step 1: 计算距离[dht3] # tile(A, reps): 构造一个矩阵,通过A重复reps次得到 # the following copy numSamples rows for dataSet diff = tile(newInput, (numSamples, 1)) - dataSet # 按元素求差值 squaredDiff = diff ** 2 #将差值平方 squaredDist = sum(squaredDiff, axis = 1) # 按行累加 distance = squaredDist ** 0.5 #将差值平方和求开方,即得距离 ## step 2: 对距离排序 # argsort() 返回排序后的索引值 sortedDistIndices = argsort(distance) classCount = {} # define a dictionary (can be append element) for i in xrange(k): ## step 3: 选择k个最近邻 voteLabel = labels[sortedDistIndices[i]] ## step 4: 计算k个最近邻中各类别出现的次数 # when the key voteLabel is not in dictionary classCount, get() # will return 0 classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 ## step 5: 返回出现次数最多的类别标签 maxCount = 0 for key, value in classCount.items(): if value > maxCount: maxCount = value maxIndex = key return maxIndex |
然后调用算法进行测试:
|
import kNN from numpy import * #生成数据集和类别标签 dataSet, labels = kNN.createDataSet() #定义一个未知类别的数据 testX = array([1.2, 1.0]) k = 3 #调用分类函数对未知数据分类 outputLabel = kNN.kNNClassify(testX, dataSet, labels, 3) print "Your input is:", testX, "and classified to class: ", outputLabel testX = array([0.1, 0.3]) outputLabel = kNN.kNNClassify(testX, dataSet, labels, 3) print "Your input is:", testX, "and classified to class: ", outputLabel |
这时候会输出
|
Your input is: [ 1.2 1.0] and classified to class: A Your input is: [ 0.1 0.3] and classified to class: B |
2.2 kNN实现手写数字识别
2.2.1 需求
利用一个手写数字“先验数据”集,使用knn算法来实现对手写数字的自动识别;
先验数据(训练数据)集:
² 数据维度比较大,样本数比较多。
² 数据集包括数字0-9的手写体。
² 每个数字大约有200个样本。
² 每个样本保持在一个txt文件中。
² 手写体图像本身的大小是32x32的二值图,转换到txt文件保存后,内容也是32x32个数字,0或者1,如下:

数据集压缩包解压后有两个目录:
² 目录trainingDigits存放的是大约2000个训练数据
² 目录testDigits存放大约900个测试数据。
2.2.2 模型分析
本案例看起来跟前一个案例几乎风马牛不相及,但是一样可以用KNN算法来实现。没错,这就是机器学习的魅力,不过,也是机器学习的难点:模型抽象能力!
思考:
1、手写体因为每个人,甚至每次写的字都不会完全精确一致,所以,识别手写体的关键是“相似度”
2、既然是要求样本之间的相似度,那么,首先需要将样本进行抽象,将每个样本变成一系列特征数据(即特征向量)
3、手写体在直观上就是一个个的图片,而图片是由上述图示中的像素点来描述的,样本的相似度其实就是像素的位置和颜色之间的组合的相似度
4、因此,将图片的像素按照固定顺序读取到一个个的向量中,即可很好地表示手写体样本
5、抽象出了样本向量,及相似度计算模型,即可应用KNN来实现
2.2.3 python实现
新建一个kNN.py脚本文件,文件里面包含四个函数:
1) 一个用来生成将每个样本的txt文件转换为对应的一个向量,
2) 一个用来加载整个数据集,
3) 一个实现kNN分类算法。
4) 最后就是实现加载、测试的函数。
|
######################################### # kNN: k Nearest Neighbors # 参数: inX: vector to compare to existing dataset (1xN) # dataSet: size m data set of known vectors (NxM) # labels: data set labels (1xM vector) # k: number of neighbors to use for comparison
# 输出: 多数类 ######################################### from numpy import * import operator import os # KNN分类核心方法 def kNNClassify(newInput, dataSet, labels, k): numSamples = dataSet.shape[0] # shape[0]代表行数 ## step 1: 计算欧式距离 # tile(A, reps): 将A重复reps次来构造一个矩阵 # the following copy numSamples rows for dataSet diff = tile(newInput, (numSamples, 1)) - dataSet # Subtract element-wise squaredDiff = diff ** 2 # squared for the subtract squaredDist = sum(squaredDiff, axis = 1) # sum is performed by row distance = squaredDist ** 0.5 ## step 2: 对距离排序 # argsort()返回排序后的索引 sortedDistIndices = argsort(distance) classCount = {} # 定义一个空的字典 for i in xrange(k): ## step 3: 选择k个最小距离 voteLabel = labels[sortedDistIndices[i]] ## step 4: 计算类别的出现次数 # when the key voteLabel is not in dictionary classCount, get() # will return 0 classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 ## step 5: 返回出现次数最多的类别作为分类结果 maxCount = 0 for key, value in classCount.items(): if value > maxCount: maxCount = value maxIndex = key return maxIndex # 将图片转换为向量 def img2vector(filename): rows = 32 cols = 32 imgVector = zeros((1, rows * cols)) fileIn = open(filename) for row in xrange(rows): lineStr = fileIn.readline() for col in xrange(cols): imgVector[0, row * 32 + col] = int(lineStr[col]) return imgVector # 加载数据集 def loadDataSet(): ## step 1: 读取训练数据集 print "---Getting training set..." dataSetDir = 'E:/Python/ml/knn/' trainingFileList = os.listdir(dataSetDir + 'trainingDigits') # 加载测试数据 numSamples = len(trainingFileList) train_x = zeros((numSamples, 1024)) train_y = [] for i in xrange(numSamples): filename = trainingFileList[i] # get train_x train_x[i, :] = img2vector(dataSetDir + 'trainingDigits/%s' % filename) # get label from file name such as "1_18.txt" label = int(filename.split('_')[0]) # return 1 train_y.append(label) ## step 2:读取测试数据集 print "---Getting testing set..." testingFileList = os.listdir(dataSetDir + 'testDigits') # load the testing set numSamples = len(testingFileList) test_x = zeros((numSamples, 1024)) test_y = [] for i in xrange(numSamples): filename = testingFileList[i] # get train_x test_x[i, :] = img2vector(dataSetDir + 'testDigits/%s' % filename) # get label from file name such as "1_18.txt" label = int(filename.split('_')[0]) # return 1 test_y.append(label) return train_x, train_y, test_x, test_y # 手写识别主流程 def testHandWritingClass(): ## step 1: 加载数据 print "step 1: load data..." train_x, train_y, test_x, test_y = loadDataSet() ## step 2: 模型训练. print "step 2: training..." pass ## step 3: 测试 print "step 3: testing..." numTestSamples = test_x.shape[0] matchCount = 0 for i in xrange(numTestSamples): predict = kNNClassify(test_x[i], train_x, train_y, 3) if predict == test_y[i]: matchCount += 1 accuracy = float(matchCount) / numTestSamples ## step 4: 输出结果 print "step 4: show the result..." print 'The classify accuracy is: %.2f%%' % (accuracy * 100) |
测试非常简单,只需要在命令行中输入:
|
import kNN kNN.testHandWritingClass() |
输出结果如下:
|
step 1: load data... ---Getting training set... ---Getting testing set... step 2: training... step 3: testing... step 4: show the result... The classify accuracy is: 98.84% |
3、KNN算法补充
3.1、k值设定为多大?
k太小,分类结果易受噪声点影响;k太大,近邻中又可能包含太多的其它类别的点。
(对距离加权,可以降低k值设定的影响)
k值通常是采用交叉检验来确定(以k=1为基准)
经验规则:k一般低于训练样本数的平方根
3.2、类别如何判定最合适?
投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法更恰当一些。而具体如何加权,需要根据具体的业务和数据特性来探索
3.3、如何选择合适的距离衡量?
高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。
变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行标准化。
3.4、训练样本是否要一视同仁?
在训练集中,有些样本可能是更值得依赖的。
也可以说是样本数据质量的问题
可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。
3.5、性能问题?
kNN是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找k个近邻)。
懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并计算距离。
已经有一些方法提高计算的效率,例如压缩训练样本量[dht4] 等。
机器学习,算法本身不是最难的,最难的是:
1、数学建模:把业务中的特性抽象成向量的过程;
2、选取适合模型的数据样本。
这两个事都不是简单的事。算法反而是比较简单的事。
数据虽然是抽象的,但其实可以映射到任意具体业务上,比如:
1、根据已毕业学生各科成绩及其就业数据来预测或引导应届毕业生生就业方向
2、根据客户各属性及其购买行为,来预测新客户的购买行为
假如:
Newinput:[1,0,2]
Dataset:
[1,0,1]
[2,1,3]
[1,0,2]
计算过程即为:
1、求差
[1,0,1] [1,0,2]
[2,1,3] -- [1,0,2]
[1,0,2] [1,0,2]
=
[0,0,-1]
[1,1,1]
[0,0,-1]
2、对差值平方
[0,0,1]
[1,1,1]
[0,0,1]
3、将平方后的差值累加
[1]
[3]
[1]
4、将上一步骤的值求开方,即得距离
[1]
[1.73]
[1]
还有诸如:
浓缩技术(condensing)
编辑技术(editing)
02-机器学习_第2天(贝叶斯分类算法与应用)
机器学习算法day02_贝叶斯分类算法及应用
课程大纲
|
朴素贝叶斯算法原理 |
Bayes算法概述 |
|
Bayes算法思想 |
|
|
Bayes算法要点 |
|
|
朴素贝叶斯算法案例1 |
需求 |
|
Python实现 |
|
|
朴素贝叶斯算法案例2 |
需求 |
|
Python实现 |
课程目标:
1、理解朴素贝叶斯算法的核心思想
2、理解朴素贝叶斯算法的代码实现
3、掌握朴素贝叶斯算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. 朴素贝叶斯分类算法原理
1.1 概述
贝叶斯分类算法是一大类分类算法的总称
贝叶斯分类算法以样本可能属于某类的概率来作为分类依据
朴素贝叶斯分类算法是贝叶斯分类算法中最简单的一种
注:朴素的意思是条件概率独立性[dht1]
1.2 算法思想
朴素贝叶斯的思想是这样的:
如果一个事物在一些属性条件发生的情况下,事物属于A的概率>属于B的概率,则判定事物属于A
通俗来说比如,你在街上看到一个黑人,我让你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?
在你的脑海中,有这么一个判断流程:
1、这个人的肤色是黑色 <特征>
2、非洲人中黑色人种概率最高 <已知的是条件概率:p(黑色|非洲人)>
而用于判断的标准是: P(非洲人|黑色)
3、没有其他辅助信息的情况下,最好的判断就是非洲人
这就是朴素贝叶斯的思想基础。
再扩展一下,假如某条街上,有100人,其中有50个美国人,50个非洲人,看到一个讲英语的黑人,那我们是怎么去判断他来自于哪里?
提取特征:
肤色: 黑
语言: 英语
先验知识:
P(黑色|非洲人) = 0.8
P(讲英语|非洲人)=0.1
P(黑色|美国人)= 0.2
P(讲英语|美国人)=0.9
要判断的概率是:
P(非洲人|(讲英语,黑色) )
P(美国人|(讲英语,黑色) )
思考过程:

P(非洲人|(讲英语,黑色) ) 的 分子= 0.1 * 0.8 *0.5 =0.04
P(美国人|(讲英语,黑色) ) 的 分子= 0.9 *0.2 * 0.5 = 0.09
从而比较这两个概率的大小就 等价于比较这两个分子的值:
可以得出结论,此人应该是 :美国人
我们的判断结果就是:此人来自美国!
其蕴含的数学原理如下:
p(A|xy)=p(Axy)/p(xy)=p(Axy)/p(x)p(y)=p(A)/p(x)*p(A)/p(y)* p(xy)/p(xy)=p(A|x)p(A|y)
|
朴素贝叶斯分类器 讲了上面的小故事,我们来朴素贝叶斯分类器的表示形式: 当特征为为x时,计算所有类别的条件概率,选取条件概率最大的类别作为待分类的类别。由于上公式的分母对每个类别都是一样的,因此计算时可以不考虑分母,即 朴素贝叶斯的朴素体现在其对各个条件的独立性假设上,加上独立假设后,大大减少了参数假设空间。
|
1.3 算法要点
1.3.1 算法步骤
1、分解各类先验样本数据中的特征
2、计算各类数据中,各特征的条件概率
(比如:特征1出现的情况下,属于A类的概率p(A|特征1),属于B类的概率p(B|特征1),属于C类的概率p(C|特征1)......)
3、分解待分类数据中的特征(特征1、特征2、特征3、特征4......)
4、计算各特征的各条件概率的乘积,如下所示:
判断为A类的概率:p(A|特征1)*p(A|特征2)*p(A|特征3)*p(A|特征4).....
判断为B类的概率:p(B|特征1)*p(B|特征2)*p(B|特征3)*p(B|特征4).....
判断为C类的概率:p(C|特征1)*p(C|特征2)*p(C|特征3)*p(C|特征4).....
......
5、结果中的最大值就是该样本所属的类别
1.3.2 算法应用举例
大众点评、淘宝等电商上都会有大量的用户评论,比如:
|
1、衣服质量太差了!!!!颜色根本不纯!!! 2、我有一有种上当受骗的感觉!!!! 3、质量太差,衣服拿到手感觉像旧货!!! 4、上身漂亮,合身,很帅,给卖家点赞 5、穿上衣服帅呆了,给点一万个赞 6、我在他家买了三件衣服!!!!质量都很差! |
0 0 0 1 1 0 |
其中1/2/3/6是差评,4/5是好评
现在需要使用朴素贝叶斯分类算法来自动分类其他的评论,比如:
|
a、这么差的衣服以后再也不买了 b、帅,有逼格 …… |
1.3.3 算法应用流程
1、分解出先验数据中的各特征
(即分词,比如“衣服”“质量太差”“差”“不纯”“帅”“漂亮”,“赞”……)
2、计算各类别(好评、差评)中,各特征的条件概率
(比如 p(“衣服”|差评)、p(“衣服”|好评)、p(“差”|好评) 、p(“差”|差评)……)
3、计算类别概率
P(好评|(c1,c2,c5,c8)) 的分子=p(“c1”|好评)*p(“c2”|好评)*……p(好评)
P(好评|(c1,c2,c5,c8)) 的分子= p(“c1”|差评)*p(“c2”|差评)*……p(差评)

5、显然P(差评)的结果值更大,因此a被判别为“差评”
2. 朴素贝叶斯分类算法案例1
2.1 需求
客户评论分类:
以在线社区的留言板为例。为了不影响社区的发展,我们要屏蔽侮辱性的言论,所以要构建一个快速过滤器,如果某条留言使用了负面或者侮辱性的语言,那么就将该留言标识为内容不当。过滤这类内容是一个很常见的需求。对此问题建立两个类别:侮辱类和非侮辱类,使用1和0分别标识。
有以下先验数据,使用bayes算法对未知类别数据分类
|
帖子内容 |
类别 |
|
'my','dog','has','flea','problems','help','please' |
0 |
|
'maybe','not','take','him','to','dog','park','stupid' |
1 |
|
'my','dalmation','is','so','cute','I','love','him' |
0 |
|
'stop','posting','stupid','worthless','garbage' |
1 |
|
'mr','licks','ate','my','steak','how','to','stop','him' |
0 |
|
'quit','buying','worthless','dog','food','stupid' |
1 |
待分类数据:
|
'love','my','dalmation' |
? |
|
'stupid','garbage' |
? |
2.2 模型分析
参见1.3.2
跟1.3.2节中的举例基本一致,中文换成英文即可
2.2 Python实现
(1) 词表到词向量的转换函数
|
from numpy import * #过滤网站的恶意留言 # 创建一个实验样本 def loadDataSet(): postingList = [['my','dog','has','flea','problems','help','please'], ['maybe','not','take','him','to','dog','park','stupid'], ['my','dalmation','is','so','cute','I','love','him'], ['stop','posting','stupid','worthless','garbage'], ['mr','licks','ate','my','steak','how','to','stop','him'], ['quit','buying','worthless','dog','food','stupid']] classVec = [0,1,0,1,0,1] return postingList, classVec # 创建一个包含在所有文档中出现的不重复词的列表 def createVocabList(dataSet): vocabSet = set([]) #创建一个空集 for document in dataSet: vocabSet = vocabSet | set(document) #创建两个集合的并集 return list(vocabSet) #将文档词条转换成词向量 def setOfWords2Vec(vocabList, inputSet): returnVec = [0]*len(vocabList) #创建一个其中所含元素都为0的向量 for word in inputSet: if word in vocabList: #returnVec[vocabList.index(word)] = 1 #index函数在字符串里找到字符第一次出现的位置 词集模型 returnVec[vocabList.index(word)] += 1 #文档的词袋模型 每个单词可以出现多次 else: print "the word: %s is not in my Vocabulary!" % word return returnVec |
(2) 从词向量计算概率
|
#朴素贝叶斯分类器训练函数 从词向量计算概率 def trainNB0(trainMatrix, trainCategory): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pAbusive = sum(trainCategory)/float(numTrainDocs) # p0Num = zeros(numWords); p1Num = zeros(numWords) #p0Denom = 0.0; p1Denom = 0.0 p0Num = ones(numWords); #避免一个概率值为0,最后的乘积也为0 p1Num = ones(numWords); #用来统计两类数据中,各词的词频 p0Denom = 2.0; #用于统计0类中的总数 p1Denom = 2.0 #用于统计1类中的总数 for i in range(numTrainDocs): if trainCategory[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) # p1Vect = p1Num / p1Denom #p0Vect = p0Num / p0Denom p1Vect = log(p1Num / p1Denom) #在类1中,每个次的发生概率 p0Vect = log(p0Num / p0Denom) #避免下溢出或者浮点数舍入导致的错误 下溢出是由太多很小的数相乘得到的 return p0Vect, p1Vect, pAbusive |
(3) 根据现实情况修改分类器
注意:主要从以下两点对分类器进行修改
① 贝叶斯概率需要计算多个概率的乘积以获得文档属于某个类别的概率,即计算p(w0|1)p(w1|1)p(w2|1)。如果其中一个概率值为0,那么最后的乘积也为0
② 第二个问题就是下溢出,这是由于太多过小的数相乘造成的。由于大部分因子都非常小,所以程序会下溢出或者得不到正确的答案。解决办法是对乘积取自然对数这样可以避免下溢出或者浮点数舍入导致的错误。
③ 每个单词的出现与否作为一个特征,被称为词集模型;在词袋模型中,每个单词可以出现多次。
|
#朴素贝叶斯分类器 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): p1 = sum(vec2Classify*p1Vec) + log(pClass1) p0 = sum(vec2Classify*p0Vec) + log(1.0-pClass1) if p1 > p0: return 1 else: return 0 def testingNB(): listOPosts, listClasses = loadDataSet() myVocabList = createVocabList(listOPosts) trainMat = [] for postinDoc in listOPosts: trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses)) testEntry = ['love','my','dalmation'] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb) testEntry = ['stupid','garbage'] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb) |
(4) 运行测试
|
>>>reload(bayes) <module ‘bayes’ from ‘bayes.py’> >>>bayes.testingNB() ['love','my','dalmation'] classified as: 0 ['stupid','garbage'] classified as: 1 |
3、朴素贝叶斯分类算法案例2
3.1 需求
利用大量邮件先验数据,使用朴素贝叶斯分类算法来自动识别垃圾邮件
3.2 python实现
|
#过滤垃圾邮件 def textParse(bigString): #正则表达式进行文本解析 import re listOfTokens = re.split(r'W*',bigString) return [tok.lower() for tok in listOfTokens if len(tok) > 2] def spamTest(): docList = []; classList = []; fullText = [] for i in range(1,26): #导入并解析文本文件 wordList = textParse(open('email/spam/%d.txt' % i).read()) docList.append(wordList) fullText.extend(wordList) classList.append(1) wordList = textParse(open('email/ham/%d.txt' % i).read()) docList.append(wordList) fullText.extend(wordList) classList.append(0) vocabList = createVocabList(docList) trainingSet = range(50);testSet = [] for i in range(10): #随机构建训练集 randIndex = int(random.uniform(0,len(trainingSet))) testSet.append(trainingSet[randIndex]) #随机挑选一个文档索引号放入测试集 del(trainingSet[randIndex]) #将该文档索引号从训练集中剔除 trainMat = []; trainClasses = [] for docIndex in trainingSet: trainMat.append(setOfWords2Vec(vocabList, docList[docIndex])) trainClasses.append(classList[docIndex]) p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses)) errorCount = 0 for docIndex in testSet: #对测试集进行分类 wordVector = setOfWords2Vec(vocabList, docList[docIndex]) if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex]: errorCount += 1 print 'the error rate is: ', float(errorCount)/len(testSet) |
此处要想真正理解,需要有概率论的基础知识
P(A|x1x2x3x4)=p(A|x1)*p(A|x2)p(A|x3)p(A|x4)则为条件概率独立
P(xy|z)=p(xyz)/p(z)=p(xz)/p(z)*p(yz)/p(z)
03-机器学习_第3天(lineage回归分类算法与应用)
机器学习算法day04_Logistic回归分类算法及应用
课程大纲
|
Logistic回归分类算法原理 |
Logistic回归分类算法概述 |
|
Logistic回归分类算法思想 |
|
|
Logistic回归分类算法分析 |
|
|
算法要点 |
|
|
Logistic回归分类算法案例 |
案例需求 |
|
Python实现 |
|
|
Sigmoid函数 |
|
|
返回回归系数 |
|
|
线性拟合线 |
|
|
Logistic回归分类算法补充 |
线性逻辑回归的数学原理 |
课程目标:
1、理解决策树算法的核心思想
2、理解决策树算法的代码实现
3、掌握决策树算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. Lineage逻辑回归分类算法
1.1 概述
Lineage逻辑回归是一种简单而又效果不错的分类算法
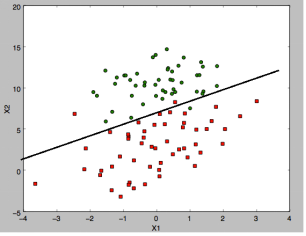
什么是回归:比如说我们有两类数据,各有50十个点组成,当我门把这些点画出来,会有一条线区分这两组数据,我们拟合出这个曲线(因为很有可能是非线性),就是回归。我们通过大量的数据找出这条线,并拟合出这条线的表达式,再有新数据,我们就以这条线为区分来实现分类。
下图是一个数据集的两组数据,中间有一条区分两组数据的线。

显然,只有这种线性可分的数据分布才适合用线性逻辑回归
1.2 算法思想
Lineage回归分类算法就是将线性回归应用在分类场景中
在该场景中,计算结果是要得到对样本数据的分类标签,而不是得到那条回归直线
1.2.1 算法图示
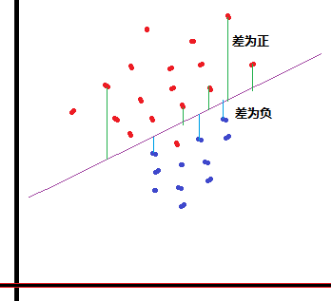
1) 算法目标()?
大白话:计算各点的y值到拟合线的垂直距离,如果
距离>0, 分为类A
距离<0, 分为类B
2) 如何得到拟合线呢?
大白话:只能先假设,因为线或面的函数都可以表达成
y(拟合)=w1*x1 + w2*x2 + w3*x3 + ...
其中的w是待定参数
而x是数据的各维度特征值
因而上述问题就变成了 样本y(x) - y(拟合) >0 ? A : B
3) 如何求解出一套最优的w参数呢?
基本思路:代入“先验数据”来逆推求解
但针对不等式求解参数极其困难
通用的解决办法,将对不等式的求解做一个转换:
- 将“样本y(x) - y(拟合) ”的差值压缩到一个0~1的小区间,
- 然后代入大量的样本特征值,从而得到一系列的输出结果;
- 再将这些输出结果跟样本的先验类别比较,并根据比较情况来调整拟合线的参数值,从而是拟合线的参数逼近最优
从而将问题转化为逼近求解的典型数学问题
1.2.2 sigmoid函数
上述算法思路中,通常使用sigmoid函数作为转换函数
l 函数表达式:
注:此处的x是向量
l 函数曲线:

之所以使用sigmoid函数,就是让样本点经过运算后得到的结果限制在0~1之间,压缩数据的巨幅震荡,从而方便得到样本点的分类标签(分类以sigmoid函数的计算结果是否大于0.5为依据)
1.3 算法实现分析
1.3.1 实现思路
v 算法思想的数学表述
把数据集的特征值设为x1,x2,x3......
求出它们的回归系数wi
设z=w1*x1+w2*x2..... ,然后将z值代入sigmoid函数并判断结果,即可得到分类标签
问题在于如何得到一组合适的参数wi?
通过解析的途径很难求解,而通过迭代的方法可以比较便捷地找到最优解
简单来说,就是不断用样本特征值代入算式,计算出结果后跟其实际标签进行比较,根据差值来修正参数,然后再代入新的样本值计算,循环往复,直到无需修正或已到达预设的迭代次数
注:此过程用梯度上升法来实现。
1.3.2梯度上升算法
梯度上升是指找到函数增长的方向。在具体实现的过程中,不停地迭代运算直到w的值几乎不再变化为止。
如图所示:

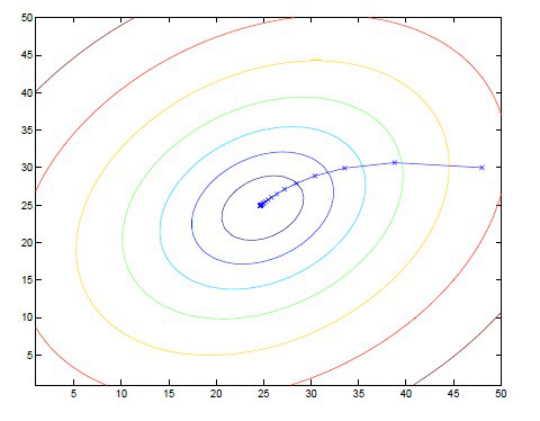
2. Lineage逻辑回归分类Python实战
2.1 需求
对给定的先验数据集,使用logistic回归算法对新数据分类

2.2 python实现
2.2.1定义sigmoid函数
|
def loadDataSet(): dataMat = []; labelMat = [] fr = open('d:/testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat,labelMat def sigmoid(inX): return 1.0/(1+exp(-inX)) |
2.2.2 返回回归系数
对应于每个特征值,for循环实现了递归梯度上升算法。
|
def gradAscent(dataMatIn, classLabels): dataMatrix = mat(dataMatIn) #将先验数据集转换为NumPy 矩阵 labelMat = mat(classLabels).transpose() #将先验数据的类标签转换为NumPy 矩阵
m,n = shape(dataMatrix) alpha = 0.001 #设置逼近步长调整系数 maxCycles = 500 #设置最大迭代次数为500 weights = ones((n,1)) #weights即为需要迭代求解的参数向量
for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #代入样本向量求得“样本y”sigmoid转换值 error = (labelMat - h) #求差 weights = weights + alpha * dataMatrix.transpose()* error #根据差值调整参数向量 return weights |
我们的数据集有两个特征值分别是x1,x2。在代码中又增设了x0变量。
结果,返回了特征值的回归系数:
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
我们得出x1和x2的关系(设x0=1),0=4.12414349+0.48007329*x1-0.6168482*x2
2.2.3 线性拟合线
画出x1与x2的关系图——线性拟合线
3、Lineage逻辑回归分类算法补充
3.1、Lineage逻辑回归的数学原理
参见《附加资料》
03-机器学习_第3天(决策树分类算法与应用)
机器学习算法day04_决策树分类算法及应用
课程大纲
|
决策树分类算法原理 |
决策树算法概述 |
|
决策树算法思想 |
|
|
决策树构造 |
|
|
算法要点 |
|
|
决策树分类算法案例 |
案例需求 |
|
Python实现 |
|
|
决策树的持久化保存 |
课程目标:
1、理解决策树算法的核心思想
2、理解决策树算法的代码实现
3、掌握决策树算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. 决策树分类算法原理
1.1 概述
决策树(decision tree)——是一种被广泛使用的分类算法。
相比贝叶斯算法,决策树的优势在于构造过程不需要任何领域知识或参数设置
在实际应用中,对于探测式的知识发现,决策树更加适用
1.2 算法思想
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是?
母亲:是,公务员不在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。
实质:通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见
假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑

上图完整表达了这个女孩决定是否见一个约会对象的策略,其中:
u 绿色节点表示判断条件
u 橙色节点表示决策结果
u 箭头表示在一个判断条件在不同情况下的决策路径
图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,如果将所有条件量化,则就变成真正的决策树了。
决策树分类算法的关键就是根据“先验数据”构造一棵最佳的决策树,用以预测未知数据的类别
决策树:是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
1.3 决策树构造
1.3.1 决策树构造样例
假如有以下判断苹果好坏的数据样本:
|
样本 红 大 好苹果 0 1 1 1 1 1 0 1 2 0 1 0 3 0 0 0 |
样本中有2个属性,A0表示是否红苹果。A1表示是否大苹果。假如要根据这个数据样本构建一棵自动判断苹果好坏的决策树。
由于本例中的数据只有2个属性,因此,我们可以穷举所有可能构造出来的决策树,就2棵,如下图所示:

显然左边先使用A0(红色)做划分依据的决策树要优于右边用A1(大小)做划分依据的决策树。
当然这是直觉的认知。而直觉显然不适合转化成程序的实现,所以需要有一种定量的考察来评价这两棵树的性能好坏。
决策树的评价所用的定量考察方法为计算每种划分情况的信息熵增益:
如果经过某个选定的属性进行数据划分后的信息熵下降最多,则这个划分属性是最优选择
1.3.2 属性划分选择(即构造决策树)的依据
熵:信息论的奠基人香农定义的用来信息量的单位。简单来说,熵就是“无序,混乱”的程度。
通过计算来理解:
1、原始样本数据的熵:
样例总数:4
好苹果:2
坏苹果:2
熵: -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1
信息熵为1表示当前处于最混乱,最无序的状态。
2、两颗决策树的划分结果熵增益计算
l 树1先选A0作划分,各子节点信息熵计算如下:
0,1叶子节点有2个正例,0个负例。信息熵为:e1 = -(2/2 * log(2/2) + 0/2 * log(0/2)) = 0。
2,3叶子节点有0个正例,2个负例。信息熵为:e2 = -(0/2 * log(0/2) + 2/2 * log(2/2)) = 0。
因此选择A0划分后的信息熵为每个子节点的信息熵所占比重的加权和:E = e1*2/4 + e2*2/4 = 0。
选择A0做划分的信息熵增益G(S, A0)=S - E = 1 - 0 = 1.
事实上,决策树叶子节点表示已经都属于相同类别,因此信息熵一定为0。
l 树2先选A1作划分,各子节点信息熵计算如下:
0,2子节点有1个正例,1个负例。信息熵为:e1 = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1。
1,3子节点有1个正例,1个负例。信息熵为:e2 = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1。
因此选择A1划分后的信息熵为每个子节点的信息熵所占比重的加权和:E = e1*2/4 + e2*2/4 = 1。也就是说分了跟没分一样!
选择A1做划分的信息熵增益G(S, A1)=S - E = 1 - 1 = 0.
因此,每次划分之前,我们只需要计算出信息熵增益最大的那种划分即可。
1.4 算法要点
1.4.1、指导思想
经过决策属性的划分后,数据的无序度越来越低,也就是信息熵越来越小
1.4.2 算法实现
梳理出数据中的属性
比较按照某特定属性划分后的数据的信息熵增益,选择信息熵增益最大的那个属性作为第一划分依据,然后继续选择第二属性,以此类推
2. 决策树分类算法Python实战
2.1 案例需求
我们的任务就是训练一个决策树分类器,输入身高和体重,分类器能给出这个人是胖子还是瘦子。
所用的训练数据如下,这个数据一共有10个样本,每个样本有2个属性,分别为身高和体重,第三列为类别标签,表示“胖”或“瘦”。该数据保存在1.txt中。
|
1.5 50 thin 1.5 60 fat 1.6 40 thin 1.6 60 fat 1.7 60 thin 1.7 80 fat 1.8 60 thin 1.8 90 fat 1.9 70 thin 1.9 80 fat |
2.2 模型分析
决策树对于“是非”的二值逻辑的分枝相当自然。而在本数据集中,身高与体重是连续值怎么办呢?
虽然麻烦一点,不过这也不是问题,只需要找到将这些连续值划分为不同区间的中间点,就转换成了二值逻辑问题。
本例决策树的任务是找到身高、体重中的一些临界值,按照大于或者小于这些临界值的逻辑将其样本两两分类,自顶向下构建决策树。
2.3 python实现
使用python的机器学习库,实现起来相当简单和优雅
|
# -*- coding: utf-8 -*- import numpy as np import scipy as sp from sklearn import tree from sklearn.metrics import precision_recall_curve from sklearn.metrics import classification_report from sklearn.cross_validation import train_test_split ''' 数据读入 ''' data = [] labels = [] with open("d:\python\ml\data\1.txt") as ifile: for line in ifile: tokens = line.strip().split(' ') data.append([float(tk) for tk in tokens[:-1]]) labels.append(tokens[-1]) x = np.array(data) labels = np.array(labels) y = np.zeros(labels.shape) ''' 标签转换为0/1 ''' y[labels=='fat']=1 ''' 拆分训练数据与测试数据 ''' x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2) ''' 使用信息熵作为划分标准,对决策树进行训练 ''' clf = tree.DecisionTreeClassifier(criterion='entropy') print(clf) clf.fit(x_train, y_train) ''' 把决策树结构写入文件 ''' with open("tree.dot", 'w') as f: f = tree.export_graphviz(clf, out_file=f) ''' 系数反映每个特征的影响力。越大表示该特征在分类中起到的作用越大 ''' print(clf.feature_importances_) '''测试结果的打印''' answer = clf.predict(x_train) print(x_train) print(answer) print(y_train) print(np.mean( answer == y_train)) '''准确率与召回率''' precision, recall, thresholds = precision_recall_curve(y_train, clf.predict(x_train)) answer = clf.predict_proba(x)[:,1] print(classification_report(y, answer, target_names = ['thin', 'fat'])) |
这时候会输出
|
[ 0.2488562 0.7511438] array([[ 1.6, 60. ], [ 1.7, 60. ], [ 1.9, 80. ], [ 1.5, 50. ], [ 1.6, 40. ], [ 1.7, 80. ], [ 1.8, 90. ], [ 1.5, 60. ]]) array([ 1., 0., 1., 0., 0., 1., 1., 1.]) array([ 1., 0., 1., 0., 0., 1., 1., 1.]) 1.0 precision recall f1-score support thin 0.83 1.00 0.91 5 fat 1.00 0.80 0.89 5 avg / total 1.00 1.00 1.00 8 array([ 0., 1., 0., 1., 0., 1., 0., 1., 0., 0.]) array([ 0., 1., 0., 1., 0., 1., 0., 1., 0., 1.]) 可以看到,对训练过的数据做测试,准确率是100%。但是最后将所有数据进行测试,会出现1个测试样本分类错误。 说明本例的决策树对训练集的规则吸收的很好,但是预测性稍微差点。 |
2.4 决策树的保存
一棵决策树的学习训练是非常耗费运算时间的,因此,决策树训练出来后,可进行保存,以便在预测新数据时只需要直接加载训练好的决策树即可
本案例的代码中已经决策树的结构写入了tree.dot中。打开该文件,很容易画出决策树,还可以看到决策树的更多分类信息。
本例的tree.dot如下所示:
|
digraph Tree { 0 [label="X[1] <= 55.0000 entropy = 0.954434002925 samples = 8", shape="box"] ; 1 [label="entropy = 0.0000 samples = 2 value = [ 2. 0.]", shape="box"] ; 0 -> 1 ; 2 [label="X[1] <= 70.0000 entropy = 0.650022421648 samples = 6", shape="box"] ; 0 -> 2 ; 3 [label="X[0] <= 1.6500 entropy = 0.918295834054 samples = 3", shape="box"] ; 2 -> 3 ; 4 [label="entropy = 0.0000 samples = 2 value = [ 0. 2.]", shape="box"] ; 3 -> 4 ; 5 [label="entropy = 0.0000 samples = 1 value = [ 1. 0.]", shape="box"] ; 3 -> 5 ; 6 [label="entropy = 0.0000 samples = 3 value = [ 0. 3.]", shape="box"] ; 2 -> 6 ; } |
根据这个信息,决策树应该长的如下这个样子:

03-机器学习_第3天(协同过滤推荐算法与应用)
机器学习算法day03_协同过滤推荐算法及应用
课程大纲
|
协同过滤推荐算法原理 |
协同过滤推荐算法概述 |
|
协同过滤推荐算法思想 |
|
|
协同过滤推荐算法分析 |
|
|
协同过滤推荐算法要点 |
|
|
协同过滤推荐算法实现 |
|
|
协同过滤推荐算法案例 |
案例需求 |
|
数据规整 |
|
|
参数设定 |
|
|
用Scikili机器学习算法库实现 |
|
|
算法检验 |
|
|
实现推荐 |
|
|
协同过滤推荐算法补充 |
计算距离的数学公式 |
|
协同过滤算法常见问题 |
课程目标:
1、理解协同过滤算法的核心思想
2、理解协同过滤算法的代码实现
3、掌握协同过滤算法的应用步骤:数据处理、建模、运算和结果判定
4、
1. CF协同过滤推荐算法原理
1.1 概述
什么是协同过滤 (Collaborative Filtering, 简称 CF)?
首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?
大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。
协同过滤算法又分为基于用户的协同过滤算法和基于物品的协同过滤算法
1.2 案例需求
如下数据是各用户对各文档的偏好:
|
用户/文档 |
文档A |
文档B |
文档C |
文档D |
|
用户A |
√ |
√ |
推荐? |
推荐? |
|
用户B |
√ |
√ |
√ |
|
|
用户C |
√ |
√ |
√ |
|
|
用户D |
√ |
√ |
现在需要基于上述数据,给A用户推荐一篇文档
1.3 算法分析
1.3.1 基于用户相似度的分析
直觉分析:“用户A/B”都喜欢物品A和物品B,从而“用户A/B”的口味最为相近
因此,为“用户A”推荐物品时可参考“用户B”的偏好,从而推荐D

这种就是基于用户的协同过滤算法UserCF指导思想
1.3.2 基于物品相似度的分析
直觉分析:物品组合(A,D)被同时偏好出现的次数最多,因而可以认为A/D两件物品的相似度最高,从而,可以为选择了A物品的用户推荐D物品

这种就是基于物品的协同过滤算法ItemCF指导思想
1.4 算法要点
1.4.1、指导思想
这种过滤算法的有效性基础在于:
1、用户偏好具有相似性,即用户可分类。这种分类的特征越明显,推荐准确率越高
2、物品之间具有相似性,即偏好某物品的人,都很可能也同时偏好另一件相似物品
1.4.2、两种CF算法适用的场景
什么情况下使用哪种算法推荐效果会更好?
不同环境下这两种理论的有效性也不同,应用时需做相应调整。
- 如豆瓣上的文艺作品,用户对其的偏好程度与用户自身的品位关联性较强;适合UserCF
- 而对于电子商务网站来说,商品之间的内在联系对用户的购买行为影响更为显著。
1.5 算法实现
总的来说,要实现协同过滤,需要一下几个步骤:
1.收集用户偏好
2.找到相似的用户或物品
3.计算推荐
1.5.1 收集用户偏好
用户有很多方式向系统提供自己的偏好信息,而且不同的应用也可能大不相同,下面举例进行介绍:
|
用户行为 |
类型 |
特征 |
作用 |
|
评分 |
显式 |
整数量化值[0,n] |
可以得到精确偏好 |
|
投票 |
显式 |
布尔量化值0|1 |
可以得到精确偏好 |
|
转发 |
显式 |
布尔量化值0|1 |
可以得到精确偏好 |
|
保存书签 |
显式 |
布尔量化值0|1 |
可以得到精确偏好 |
|
标记书签Tag |
显式 |
一些单词 |
需要进一步分析得到偏好 |
|
评论 |
显式 |
一些文字 |
需要进一步分析得到偏好 |
|
点击流 |
隐式 |
一组点击记录 |
需要进一步分析得到偏好 |
|
页面停留时间 |
隐式 |
一组时间信息 |
噪音偏大,不好利用 |
|
购买 |
隐式 |
布尔量化值0|1 |
可以得到精确偏好 |
1.5.2 原始偏好数据的预处理
v 用户行为识别/组合
在一般应用中,我们提取的用户行为一般都多于一种,关于如何组合这些不同的用户行为,比如,可以将用户行为分为“查看”和“购买”等等,然后基于不同的行为,计算不同的用户 / 物品相似度。
类似于当当网或者京东给出的“购买了该图书的人还购买了 ...”,“查看了图书的人还查看了 ...”
v 喜好程度加权
根据不同行为反映用户喜好的程度将它们进行加权,得到用户对于物品的总体喜好。
一般来说,显式的用户反馈比隐式的权值大,但比较稀疏,毕竟进行显示反馈的用户是少数;同时相对于“查看”,“购买”行为反映用户喜好的程度更大,但这也因应用而异。
v 数据减噪和归一化。
① 减噪:用户行为数据是用户在使用应用过程中产生的,它可能存在大量的噪音和用户的误操作,我们可以通过经典的数据挖掘算法过滤掉行为数据中的噪音,这样可以是我们的分析更加精确。
② 归一化:如前面讲到的,在计算用户对物品的喜好程度时,可能需要对不同的行为数据进行加权。但可以想象,不同行为的数据取值可能相差很大,比如,用户的查看数据必然比购买数据大的多,如何将各个行为的数据统一在一个相同的取值范围中,从而使得加权求和得到的总体喜好更加精确,就需要我们进行归一化处理。最简单的归一化处理,就是将各类数据除以此类中的最大值,以保证归一化后的数据取值在 [0,1] 范围中。
v 形成用户偏好矩阵
一般是二维矩阵,一维是用户列表,另一维是物品列表,值是用户对物品的偏好,一般是 [0,1] 或者 [-1, 1] 的浮点数值。
1.5.3 找到相似用户或物品
当已经对用户行为进行分析得到用户喜好后,我们可以根据用户喜好计算相似用户和物品,然后基于相似用户或者物品进行推荐,这就是最典型的 CF 的两个分支:基于用户的 CF 和基于物品的 CF。这两种方法都需要计算相似度,下面我们先看看最基本的几种计算相似度的方法。
1.5.4 相似度的计算
相似度的计算,现有的几种基本方法都是基于向量(Vector)的,其实也就是计算两个向量的距离,距离越近相似度越大。
在推荐的场景中,在用户 - 物品偏好的二维矩阵中,我们可以将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,或者将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度。
CF的常用方法有三种,分别是欧式距离法、皮尔逊相关系数法、余弦相似度法。
为了测试算法,给出以下简单的用好偏好数据矩阵:
行表示三名用户,列表示三个品牌,对品牌的喜爱度按照1~5增加。
|
用户 |
苹果 |
小米 |
魅族 |
|
zhangsan |
5 |
5 |
2 |
|
Lisi |
3 |
5 |
4 |
|
wangwu |
1 |
2 |
5 |
(1)欧氏距离法
就是计算每两个点的距离,比如Nike和Sony的相似度 。
数值越小,表示相似度越高。
|
def OsDistance(vector1, vector2): sqDiffVector = vector1-vector2 sqDiffVector=sqDiffVector**2 sqDistances = sqDiffVector.sum() distance = sqDistances**0.5 return distance |
(2)皮尔逊相关系数
两个变量之间的相关系数越高,从一个变量去预测另一个变量的精确度就越高,这是因为相关系数越高,就意味着这两个变量的共变部分越多,所以从其中一个变量的变化就可越多地获知另一个变量的变化。如果两个变量之间的相关系数为1或-1,那么你完全可由变量X去获知变量Y的值。
· 当相关系数为0时,X和Y两变量无关系。
· 当X的值增大,Y也增大,正相关关系,相关系数在0.00与1.00之间
· 当X的值减小,Y也减小,正相关关系,相关系数在0.00与1.00之间
· 当X的值增大,Y减小,负相关关系,相关系数在-1.00与0.00之间
当X的值减小,Y增大,负相关关系,相关系数在-1.00与0.00之间
相关系数的绝对值越大,相关性越强,相关系数越接近于1和-1,相关度越强,相关系数越接近于0,相关度越弱。
在python中用函数corrcoef实现,具体方法见参考资料
(3)余弦相似度
通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相
反的方向时,余弦相似度的值为-1。在比较过程中,向量的规模大小不予考虑,仅仅考虑到向量的指向方向。余弦相似度通常用于两个向量的夹角小于90°之内,因此余弦相似度的值为0到1之间。
|
def cosSim(inA,inB): num = float(inA.T*inB) denom = la.norm(inA)*la.norm(inB) return 0.5+0.5*(num/denom) |
注:本课程的实战案例基于皮尔逊相关系数法实现
1.5.3 计算推荐
UserCF基于用户相似度的推荐
计算推荐的过程其实就是KNN算法的计算过程
ItemCF基于物品相似度的推荐
算法思路
1. 构建物品的同现矩阵
2. 构建用户对物品的评分矩阵
3. 通过矩阵计算得出推荐结果
推荐结果=用户评分矩阵*同现矩阵
实质:计算各种物品组合的出现次数

2. CF协同过滤算法Python实战
2.1 电影推荐需求
根据一个用户对电影评分的数据集来实现基于用户相似度的协同过滤算法推荐,相似度的算法采用皮尔逊相关系数法
数据样例如下:
用户ID:电影ID:评分:时间
|
1::1193::5::978300760 1::661::3::978302109 1::914::3::978301968 1::3408::4::978300275 1::2355::5::978824291 1::1197::3::978302268 1::1287::5::978302039 1::2804::5::978300719 1::594::4::978302268 1::919::4::978301368 |
2.2 算法实现
本案例使用的数据分析包为pandas,Numpy和matplotlib
2.2.1 数据规整
首先将评分数据从ratings.dat中读出到一个DataFrame 里:
|
>>> import pandas as pd >>> from pandas import Series,DataFrame >>> rnames = ['user_id','movie_id','rating','timestamp'] >>> ratings = pd.read_table(r'ratings.dat',sep='::',header=None,names=rnames) >>> ratings[:3] user_id movie_id rating timestamp 0 1 1193 5 978300760 1 1 661 3 978302109 2 1 914 3 978301968 [3 rows x 4 columns] |
ratings 表中对我们有用的仅是 user_id、movie_id 和 rating 这三列,因此我们将这三列取出,放到一个以 user 为行,movie 为列,rating 为值的表 data 里面。
|
>>> data = ratings.pivot(index='user_id',columns='movie_id',values='rating') #形成一个透视表 >>> data[:5] |

可以看到这个表相当得稀疏,填充率大约只有 5%,接下来要实现推荐的第一步是计算 user 之间的相关系数
2.2.2 相关度测算
DataFrame对象有一个很亲切的方法:
.corr(method='pearson', min_periods=1) 方法,可以对所有列互相计算相关系数。
其中:
method默认为皮尔逊相关系数,
min_periods参数,这个参数的作用是设定计算相关系数时的最小样本量,低于此值的一对列将不进行运算。这个值的取舍关系到相关系数计算的准确性,因此有必要先来确定一下这个参数。
2.2.3 min_periods 参数测定
测定这样一个参数的基本方法:
v 统计在 min_periods 取不同值时,相关系数的标准差大小,越小越好;
但同时又要考虑到,我们的样本空间十分稀疏,min_periods 定得太高会导致出来的结果集太小,所以只能选定一个折中的值。
这里我们测定评分系统标准差的方法为:
v 在 data中挑选一对重叠评分最多的用户,用他们之间的相关系数的标准差去对整体标准差做点估计。
在此前提下对这一对用户在不同样本量下的相关系数进行统计,观察其标准差变化。
首先,要找出重叠评分最多的一对用户。我们新建一个以 user 为行列的方阵 foo,然后挨个填充不同用户间重叠评分的个数:
|
>>> foo = DataFrame(np.empty((len(data.index),len(data.index)),dtype=int),index=data.index,columns=data.index) #print(empt.shape): (6040, 6040) >>> for i in foo.index: for j in foo.columns: foo.ix[i,j] = data.ix[i][data.ix[j].notnull()].dropna().count() |
这段代码特别费时间,因为最后一行语句要执行 4000*4000 = 1600万遍;
找到的最大值所对应的行列分别为 424 和 4169,这两位用户之间的重叠评分数为 998:
|
>>> for i in foo.index: foo.ix[i,i]=0 #先把对角线的值设为 0 >>> ser = Series(np.zeros(len(foo.index))) >>> for i in foo.index: ser[i]=foo[i].max() #计算每行中的最大值 >>> ser.idxmax() #返回ser的最大值所在的行号 4169 >>> ser[4169] #取得最大值 998 >>> foo[foo==998][4169].dropna() #取得另一个 user_id 424 4169 Name: user_id, dtype: float64 |
把 424 和 4169 的评分数据单独拿出来,放到一个名为 test 的表里,另外计算了一下这两个用户之间的相关系数为 0.456,还算不错,另外通过柱状图了解一下他俩的评分分布情况:
|
>>> data.ix[4169].corr(data.ix[424]) 0.45663851303413217 >>> test = data.reindex([424,4169],columns=data.ix[4169][data.ix[424].notnull()].dropna().index) >>> test movie_id 2 6 10 11 12 17 ... 424 4 4 4 4 1 5 ... 4169 3 4 4 4 2 5 ... >>> test.ix[424].value_counts(sort=False).plot(kind='bar') >>> test.ix[4169].value_counts(sort=False).plot(kind='bar') |
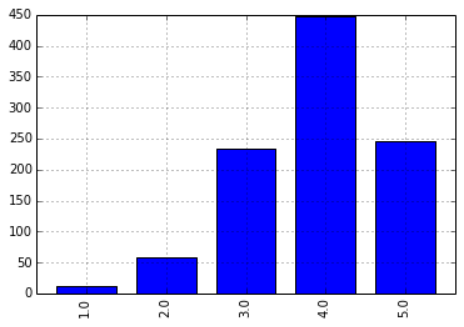

对这俩用户的相关系数统计,我们分别随机抽取 20、50、100、200、500 和 998 个样本值,各抽 20 次。并统计结果:
|
>>> periods_test = DataFrame(np.zeros((20,7)),columns=[10,20,50,100,200,500,998]) >>> for i in periods_test.index: for j in periods_test.columns: sample = test.reindex(columns=np.random.permutation(test.columns)[:j]) periods_test.ix[i,j] = sample.iloc[0].corr(sample.iloc[1]) >>> periods_test[:5] 10 20 50 100 200 500 998 0 -0.306719 0.709073 0.504374 0.376921 0.477140 0.426938 0.456639 1 0.386658 0.607569 0.434761 0.471930 0.437222 0.430765 0.456639 2 0.507415 0.585808 0.440619 0.634782 0.490574 0.436799 0.456639 3 0.628112 0.628281 0.452331 0.380073 0.472045 0.444222 0.456639 4 0.792533 0.641503 0.444989 0.499253 0.426420 0.441292 0.456639 [5 rows x 7 columns] >>> periods_test.describe() 10 20 50 100 200 500 #998略 count 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000 mean 0.346810 0.464726 0.458866 0.450155 0.467559 0.452448 std 0.398553 0.181743 0.103820 0.093663 0.036439 0.029758 min -0.444302 0.087370 0.192391 0.242112 0.412291 0.399875 25% 0.174531 0.320941 0.434744 0.375643 0.439228 0.435290 50% 0.487157 0.525217 0.476653 0.468850 0.472562 0.443772 75% 0.638685 0.616643 0.519827 0.500825 0.487389 0.465787 max 0.850963 0.709073 0.592040 0.634782 0.546001 0.513486 [8 rows x 7 columns] |
从 std 这一行来看,理想的 min_periods 参数值应当为 200 左右(标准差和均值、极值最接近)。
2.2.3 算法检验
为了确认在 min_periods=200 下本推荐算法的靠谱程度,最好还是先做个检验。
具体方法为:在评价数大于 200 的用户中随机抽取 1000 位用户,每人随机提取一个评价另存到一个数组里,并在数据表中删除这个评价。然后基于阉割过的数据表计算被提取出的 1000 个评分的期望值,最后与真实评价数组进行相关性比较,看结果如何。
|
>>> check_size = 1000 >>> check = {} >>> check_data = data.copy() #复制一份 data 用于检验,以免篡改原数据 >>> check_data = check_data.ix[check_data.count(axis=1)>200] #滤除评价数小于200的用户 >>> for user in np.random.permutation(check_data.index): movie = np.random.permutation(check_data.ix[user].dropna().index)[0] check[(user,movie)] = check_data.ix[user,movie] check_data.ix[user,movie] = np.nan check_size -= 1 if not check_size: break >>> corr = check_data.T.corr(min_periods=200) >>> corr_clean = corr.dropna(how='all') >>> corr_clean = corr_clean.dropna(axis=1,how='all') #删除全空的行和列 >>> check_ser = Series(check) #这里是被提取出来的 1000 个真实评分 >>> check_ser[:5] (15, 593) 4 (23, 555) 3 (33, 3363) 4 (36, 2355) 5 (53, 3605) 4 dtype: float64 |
接下来要基于corr_clean 给 check_ser 中的 1000 个用户-影片对计算评分期望。
计算方法为:对与用户相关系数大于 0.1 的其他用户评分进行加权平均,权值为相关系数
|
>>> result = Series(np.nan,index=check_ser.index) >>> for user,movie in result.index: #这个循环看着很乱,实际内容就是加权平均而已 prediction = [] if user in corr_clean.index: corr_set = corr_clean[user][corr_clean[user]>0.1].dropna() #仅限大于 0.1 的用户 else:continue for other in corr_set.index: if not np.isnan(data.ix[other,movie]) and other != user:#注意bool(np.nan)==True prediction.append((data.ix[other,movie],corr_set[other])) if prediction: result[(user,movie)] = sum([value*weight for value,weight in prediction])/sum([pair[1] for pair in prediction]) >>> result.dropna(inplace=True) >>> len(result)#随机抽取的 1000 个用户中也有被 min_periods=200 刷掉的 862 >>> result[:5] (23, 555) 3.967617 (33, 3363) 4.073205 (36, 2355) 3.903497 (53, 3605) 2.948003 (62, 1488) 2.606582 dtype: float64 >>> result.corr(check_ser.reindex(result.index)) 0.436227437429696 >>> (result-check_ser.reindex(result.index)).abs().describe()#推荐期望与实际评价之差的绝对值 count 862.000000 mean 0.785337 std 0.605865 min 0.000000 25% 0.290384 50% 0.686033 75% 1.132256 max 3.629720 dtype: float64 |
862 的样本量能达到 0.436 的相关系数,应该说结果还不错。如果一开始没有滤掉评价数小于 200 的用户的话,那么首先在计算 corr 时会明显感觉时间变长,其次 result 中的样本量会很小,大约 200+个。但因为样本量变小的缘故,相关系数可以提升到 0.5~0.6 。
另外从期望与实际评价的差的绝对值的统计量上看,数据也比较理想。
2.2.4 实现推荐
在上面的检验,尤其是平均加权的部分做完后,推荐的实现就没有什么新东西了。
首先在原始未阉割的 data 数据上重做一份 corr 表:
|
>>> corr = data.T.corr(min_periods=200) >>> corr_clean = corr.dropna(how='all') >>> corr_clean = corr_clean.dropna(axis=1,how='all') |
我们在 corr_clean 中随机挑选一位用户为他做一个推荐列表:
|
>>> lucky = np.random.permutation(corr_clean.index)[0] >>> gift = data.ix[lucky] >>> gift = gift[gift.isnull()] #现在 gift 是一个全空的序列 |
最后的任务就是填充这个 gift:
|
>>> corr_lucky = corr_clean[lucky].drop(lucky)#lucky 与其他用户的相关系数 Series,不包含 lucky 自身 >>> corr_lucky = corr_lucky[corr_lucky>0.1].dropna() #筛选相关系数大于 0.1 的用户 >>> for movie in gift.index: #遍历所有lucky没看过的电影 prediction = [] for other in corr_lucky.index: #遍历所有与lucky 相关系数大于 0.1 的用户 if not np.isnan(data.ix[other,movie]): prediction.append((data.ix[other,movie],corr_clean[lucky][other])) if prediction: gift[movie] = sum([value*weight for value,weight in prediction])/sum([pair[1] for pair in prediction]) >>> gift.dropna().order(ascending=False) #将 gift 的非空元素按降序排列 movie_id 3245 5.000000 2930 5.000000 2830 5.000000 2569 5.000000 1795 5.000000 981 5.000000 696 5.000000 682 5.000000 666 5.000000 572 5.000000 1420 5.000000 3338 4.845331 669 4.660464 214 4.655798 3410 4.624088 ... 2833 1 2777 1 2039 1 1773 1 1720 1 1692 1 1538 1 1430 1 1311 1 1164 1 843 1 660 1 634 1 591 1 56 1 Name: 3945, Length: 2991, dtype: float64 |
3、CF协同过滤算法补充
3.1、计算距离的数学公式
欧几里德距离(Euclidean Distance)
最初用于计算欧几里德空间中两个点的距离,假设 x,y 是 n 维空间的两个点,它们之间的欧几里德距离是:
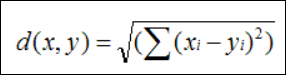
可以看出,当 n=2 时,欧几里德距离就是平面上两个点的距离。
当用欧几里德距离表示相似度,一般采用以下公式进行转换:距离越小,相似度越大
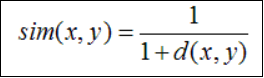
皮尔逊相关系数(Pearson Correlation Coefficient)
皮尔逊相关系数一般用于计算两个定距变量间联系的紧密程度,它的取值在 [-1,+1] 之间。
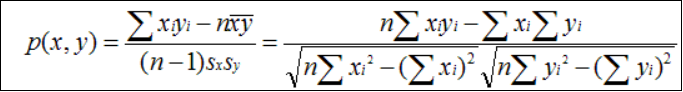
sx, sy是 x 和 y 的样品标准偏差。
Cosine 相似度(Cosine Similarity)
Cosine 相似度被广泛应用于计算文档数据的相似度:

Tanimoto 系数(Tanimoto Coefficient)
Tanimoto 系数也称为 Jaccard 系数,是 Cosine 相似度的扩展,也多用于计算文档数据的相似度:

相似邻居的计算
介绍完相似度的计算方法,下面我们看看如何根据相似度找到用户-物品的邻居,常用的挑选邻居的原则可以分为两类:
1) 固定数量的邻居:K-neighborhoods 或者 Fix-size neighborhoods
不论邻居的“远近”,只取最近的 K 个,作为其邻居。
如下图中的 A,假设要计算点 1 的 5- 邻居,那么根据点之间的距离,我们取最近的 5 个点,分别是点 2,点 3,点 4,点 7 和点 5。但很明显我们可以看出,这种方法对于孤立点的计算效果不好,因为要取固定个数的邻居,当它附近没有足够多比较相似的点,就被迫取一些不太相似的点作为邻居,这样就影响了邻居相似的程度,比如下图中,点 1 和点 5 其实并不是很相似。
2) 基于相似度门槛的邻居:Threshold-based neighborhoods
与计算固定数量的邻居的原则不同,基于相似度门槛的邻居计算是对邻居的远近进行最大值的限制,落在以当前点为中心,距离为 K 的区域中的所有点都作为当前点的邻居,这种方法计算得到的邻居个数不确定,但相似度不会出现较大的误差。
如下图中的 B,从点 1 出发,计算相似度在 K 内的邻居,得到点 2,点 3,点 4 和点 7,这种方法计算出的邻居的相似度程度比前一种优,尤其是对孤立点的处理。
图:相似邻居计算示意图

3.2、协同过滤算法常见问题
虽然协同过滤是一种比较省事的推荐方法,但在某些场合下并不如利用元信息推荐好用。协同过滤会遇到的两个常见问题是
1) 稀疏性问题——因用户做出评价过少,导致算出的相关系数不准确
2) 冷启动问题——因物品获得评价过少,导致无“权”进入推荐列表中
都是样本量太少导致的(上例中也使用了至少 200 的有效重叠评价数)。
因此在对于新用户和新物品进行推荐时,使用一些更一般性的方法效果可能会更好。比如:
v 给新用户推荐更多平均得分超高的电影;
v 把新电影推荐给喜欢类似电影(如具有相同导演或演员)的人。
后面这种做法需要维护一个物品分类表,这个表既可以是基于物品元信息划分的,也可是通过聚类得到的。

