这里总结复习一下最短路的四种算法
------------------------------------------------
以下题目过于占用篇幅,请自行上OJ看题
1)Floyd算法
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。(百度百科)
重点是多源点。
邻接矩阵 mp[i][j] 表示的是从 i 点到 j 点的权值,现在在 i 到 j 之间插一个 k 点,那么状态转移方程为 mp[i][j] = min(mp[i][k] + mp[k][j], mp[i][j]);
这算法缺点是时间复杂度大,好像一个图到 500 个点就会爆时间了。。。。
核心代码
1 for(int k = 1;k <= n;++k) 2 for(int i = 1;i <= n;++i) 3 for(int j = 1;j <= n;++j) 4 mp[i][j] = min(mp[i][k] + mp[k][j], mp[i][j]);
HDU1874 畅通工程续(这题有几个坑点注意一下就好)
这里用Floyd算法AC

1 #include <iostream> 2 #include <cstdio> 3 #include <string> 4 #include <cstring> 5 #include <cmath> 6 #include <sstream> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <vector> 11 #include <queue> 12 #include <iomanip> 13 #include <stack> 14 15 using namespace std; 16 17 typedef long long LL; 18 const int INF = 0x3f3f3f3f; 19 const int MAXN = 100005; 20 const int MOD = 1e9 + 7; 21 22 #define MemN(x) memset(x, -1, sizeof(x)) 23 #define Mem0(x) memset(x, 0, sizeof(x)) 24 #define MemM(x) memset(x, 0x3f, sizeof(x)) 25 26 int main() 27 { 28 int n, m, dp[205][205]; 29 int a, b, c; 30 while(cin >> n >> m) 31 { 32 MemM(dp); 33 int i, j, k; 34 for(i = 0;i < n;++i) 35 dp[i][i] = 0; 36 for(i = 0;i < m;++i) 37 { 38 cin >> a >> b >> c; 39 dp[a][b] = min(dp[a][b], c); 40 dp[b][a] = dp[a][b]; 41 } 42 43 for(k = 0;k < n;++k) 44 for(i = 0;i < n;++i) 45 for(j = 0;j < n;++j) 46 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]); 47 cin >> a >> b; 48 if(dp[a][b] != INF) 49 cout << dp[a][b] << endl; 50 else 51 cout << -1 << endl; 52 } 53 }
2)Dijkstra算法(没错,写 Dijkstra 比写 迪杰斯特拉 看起来更厉害的样子)
这里先介绍基础的 Dijkstra 算法,文章后面再说 Dijkstra 算法的优化。注意 Dijkstra 算法只适用无负权值的单源点最短路。这个算法跟最小生成树的 Prim算法 类似。
Dijkstra 算法的核心思想是:松弛。例如有 a, b, c , d 三个点,有三条边 a -> b = 1, a -> c = 5, b ->c = 2, c -> d = 1(我不会画画,就文字说明了)
从 a 开始,所以 dis[b] = 1, dis[c] = 5,dis[d] = ∞
然后选出最短的边 mi = 1,对应点为 b,就以 b 为中点松弛,即从 a -> c 跟 a ->b -> c比较
dis[c] = min(dis[c], mi + mp[b][c]),下面 a -> d 类似
dis[d] = min(dis[d], mi + mp[b][d]) 这样更新 dis,具体看代码吧
核心代码
1 int dis[MAXN], n, mp[MAXN][MAXN]; 2 bool vis[MAXN]; 3 //从 s 点开始的单源最短路 4 void Dijkstra(int s) 5 { 6 memset(vis, 0, sizeof(vis)); 7 int i, j; 8 for(i = 1;i <= n;++i) 9 dis[i] = mp[s][i]; 10 vis[s] = 1; 11 int v, mi; 12 //每次都 vis 一个点,加上上面一次 vis, 所以一共 vis n次 13 for(i = 1;i < n;++i) 14 { 15 //选出当前离 s 最近的点 16 mi = INF; 17 for(j = 1;j <= n;++j) 18 { 19 if(!vis[j] && dis[j] < mi) 20 { 21 mi = dis[j]; 22 v = j; 23 } 24 } 25 vis[v] = 1; 26 //更新 dis 27 for(j = 1;j <= n;++j) 28 if(!vis[j] && mi + mp[v][j] < dis[j]) 29 dis[j] = mi + mp[v][j]; 30 } 31 }
上面那道杭电也可以用Dijkstra 算法做做看,这里给出另一道题
POJ-2387 Til the Cows Come Home
Dijkstra算法 AC

1 #include <iostream> 2 #include <cstdio> 3 #include <string> 4 #include <cstring> 5 #include <cmath> 6 #include <sstream> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <vector> 11 #include <queue> 12 #include <iomanip> 13 #include <stack> 14 15 using namespace std; 16 17 typedef long long LL; 18 //我也不知道为什么这里改成这个就能过,之前那个 0x3f3f3f3f 不会爆 int 啊,坑我 WA 到绝望 19 const int INF = 999999999; 20 const int MAXN = 1005; 21 const int MOD = 1e9 + 7; 22 23 #define MemI(x) memset(x, -1, sizeof(x)) 24 #define Mem0(x) memset(x, 0, sizeof(x)) 25 #define MemM(x) memset(x, 0x3f, sizeof(x)) 26 27 int dis[MAXN], n, mp[MAXN][MAXN]; 28 bool vis[MAXN]; 29 //从 s 点开始的单源最短路 30 void Dijkstra(int s) 31 { 32 memset(vis, 0, sizeof(vis)); 33 int i, j; 34 for(i = 1;i <= n;++i) 35 dis[i] = mp[s][i]; 36 vis[s] = 1; 37 int v, mi; 38 //每次都 vis 一个点,加上上面一次 vis, 所以一共 vis n次 39 for(i = 1;i < n;++i) 40 { 41 //选出当前离 s 最近的点 42 mi = INF; 43 for(j = 1;j <= n;++j) 44 { 45 if(!vis[j] && dis[j] < mi) 46 { 47 mi = dis[j]; 48 v = j; 49 } 50 } 51 vis[v] = 1; 52 //更新 dis 53 for(j = 1;j <= n;++j) 54 if(!vis[j] && (mi + mp[v][j]) < dis[j]) 55 dis[j] = mi + mp[v][j]; 56 } 57 } 58 59 int main() 60 { 61 int T; 62 while(scanf("%d%d", &T, &n) != EOF) 63 { 64 for(int i = 1;i <= n;++i) 65 { 66 for(int j = 1;j <= n;++j) 67 { 68 if(i != j) 69 mp[i][j] = INF; 70 else 71 mp[i][j] = 0; 72 } 73 } 74 int a, b, c; 75 while(T--) 76 { 77 scanf("%d%d%d", &a, &b, &c); 78 if(c < mp[a][b]) 79 mp[a][b] = mp[b][a] = c; 80 } 81 Dijkstra(n); 82 printf("%d ", dis[1]); 83 } 84 return 0; 85 }
另:这里给出另一道题POJ-2253 Frogger
虽然不是求最短路,但是可以用 Dijkstra算法,至于为什么能用它?
考虑目前最短路的两种算法:Floyd 算法,和 Dijkstra 算法,前者是可以说是直接求a 到 b 的距离,并没有涉及到经过过程,但是后者涉及到经过过程,所以有时候求路径过程的最大值或最小值可以考虑 Dijkstra算法,下面Dijkstra算法AC代码

1 #include <iostream> 2 #include <cstdio> 3 #include <string> 4 #include <cstring> 5 #include <cmath> 6 #include <sstream> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <vector> 11 #include <queue> 12 #include <iomanip> 13 #include <stack> 14 15 using namespace std; 16 17 typedef long long LL; 18 const int INF = 0x3f3f3f3f; 19 const int MAXN = 205; 20 const int MOD = 1e9 + 7; 21 22 #define MemI(x) memset(x, -1, sizeof(x)) 23 #define Mem0(x) memset(x, 0, sizeof(x)) 24 #define MemM(x) memset(x, 0x3f, sizeof(x)) 25 26 struct Node 27 { 28 int x, y; 29 }node[MAXN]; 30 double mp[MAXN][MAXN], dis[MAXN]; 31 int n; 32 bool vis[MAXN]; 33 34 double Cal(int x1, int y1, int x2, int y2) 35 { 36 return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)); 37 } 38 39 void Dijkstra() 40 { 41 Mem0(vis); 42 double mi; 43 int i, j, v; 44 for(i = 1;i <= n;++i) 45 dis[i] = mp[1][i]; 46 vis[1] = true; 47 for(i = 1;i < n;++i) 48 { 49 mi = INF; 50 for(j = 1;j <= n;++j) 51 if(!vis[j] && dis[j] < mi) 52 { 53 mi = dis[j]; 54 v = j; 55 } 56 vis[v] = true; 57 //dis 表示该路径上的最大的一段 58 for(j = 1;j <= n;++j) 59 if(!vis[j] && mp[v][j] < dis[j]) 60 dis[j] = max(mi, mp[v][j]); 61 62 } 63 } 64 65 int main() 66 { 67 int cnt = 1; 68 while(scanf("%d", &n) != EOF && n) 69 { 70 int i, j, k; 71 for(i = 1;i <= n;++i) 72 scanf("%d%d", &node[i].x, &node[i].y); 73 //存点与点的距离 74 for(i = 1;i <= n;++i) 75 for(j = 1;j <= n;++j) 76 mp[i][j] = Cal(node[i].x, node[i].y, node[j].x, node[j].y); 77 78 Dijkstra(); 79 if(cnt != 1) 80 printf(" "); 81 printf("Scenario #%d Frog Distance = %.3f ", cnt++, dis[2]); 82 } 83 return 0; 84 }
Floyd算法也算 dp 的一种,所以更改一下 dp 条件也是可以做的(手动滑稽),下面Floyd算法AC,根据OJ反应,这里Floyd算法的时间是Dijkstra算法的6倍

1 #include <iostream> 2 #include <cstdio> 3 #include <string> 4 #include <cstring> 5 #include <cmath> 6 #include <sstream> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <vector> 11 #include <queue> 12 #include <iomanip> 13 #include <stack> 14 15 using namespace std; 16 17 typedef long long LL; 18 const int INF = 0x3f3f3f3f; 19 const int MAXN = 205; 20 const int MOD = 1e9 + 7; 21 22 #define MemI(x) memset(x, -1, sizeof(x)) 23 #define Mem0(x) memset(x, 0, sizeof(x)) 24 #define MemM(x) memset(x, 0x3f, sizeof(x)) 25 26 struct Node 27 { 28 int x, y; 29 }node[MAXN]; 30 double mp[MAXN][MAXN], dis[MAXN]; 31 int n; 32 bool vis[MAXN]; 33 34 double Cal(int x1, int y1, int x2, int y2) 35 { 36 return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)); 37 } 38 39 void Dijkstra() 40 { 41 Mem0(vis); 42 double mi; 43 int i, j, v; 44 for(i = 1;i <= n;++i) 45 dis[i] = mp[1][i]; 46 vis[1] = true; 47 for(i = 1;i < n;++i) 48 { 49 mi = INF; 50 for(j = 1;j <= n;++j) 51 if(!vis[j] && dis[j] < mi) 52 { 53 mi = dis[j]; 54 v = j; 55 } 56 vis[v] = true; 57 //dis 表示该路径上的最大的一段 58 for(j = 1;j <= n;++j) 59 if(!vis[j] && mp[v][j] < dis[j]) 60 dis[j] = max(mi, mp[v][j]); 61 62 } 63 printf("%.3f ", dis[2]); 64 } 65 66 void Floyd() 67 { 68 for(int k = 1;k <= n;++k) 69 for(int i = 1;i <= n;++i) 70 for(int j = 1;j <= n;++j) 71 if(mp[i][k] < mp[i][j] && mp[k][j] < mp[i][j]) 72 mp[i][j] = max(mp[i][k], mp[k][j]); 73 printf("%.3f ", mp[1][2]); 74 } 75 76 int main() 77 { 78 int cnt = 1; 79 while(scanf("%d", &n) != EOF && n) 80 { 81 int i, j, k; 82 for(i = 1;i <= n;++i) 83 scanf("%d%d", &node[i].x, &node[i].y); 84 //存点与点的距离 85 for(i = 1;i <= n;++i) 86 for(j = 1;j <= n;++j) 87 mp[i][j] = Cal(node[i].x, node[i].y, node[j].x, node[j].y); 88 if(cnt != 1) 89 printf(" "); 90 printf("Scenario #%d Frog Distance = ", cnt++); 91 // Dijkstra(); 92 Floyd(); 93 } 94 return 0; 95 }
3)Bellman-Ford 算法
这篇博客比较清楚,可以去看一下
https://www.cnblogs.com/godfray/p/4077146.html
Bellman - ford算法是求含负权图的单源最短路径的一种算法,Dijkstra算法无法判断含负权边的图的最短路。Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路问题。对图G运行Bellman - Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。(百度百科)
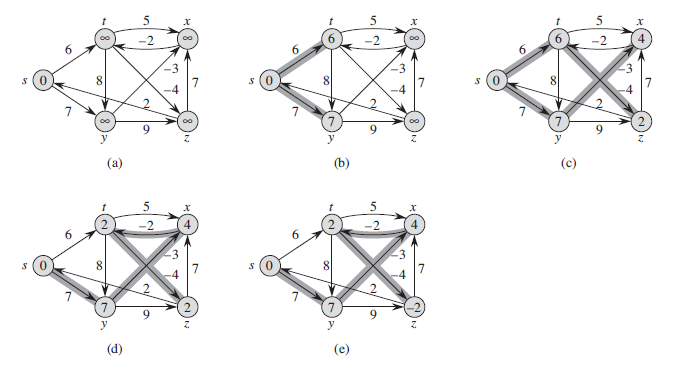
给模板啦
1 //从 u 到 v 的权值为 w 2 struct Edge 3 { 4 int u, v, w; 5 }edge[MAXN]; 6 //n 个点 m 条边 7 int n, m, dis[MAXN]; 8 9 bool Bellman_Ford(int s) 10 { 11 int i, j; 12 //初始化,如上图 13 for(i = 1;i <= n;++i) 14 dis[i] = INF; 15 dis[s] = 0; 16 //然后像图那样 bfs,最坏情况是每次 bfs 都只遍历到一个点, 17 //所以除源点外最多遍历 n - 1 次,就得到到该点的最短路 18 //关于转移方程,可以理解成 s -> u -> v 跟 s -> v 比较 19 for(i = 1;i < n;++i) 20 for(j = 0;j < m;++j) 21 if(dis[edge[j].v] > dis[edge[j].u] + edge[j].w) 22 dis[edge[j].v] = dis[edge[j].u] + edge[j].w; 23 //上面的过程已经将所有点都变成最短路了,负权回路除外 24 //因为如果在负权回路中无限循环,那么最短路将是无穷小 25 //即如果还存在可以松弛的边,即存在负权回路 26 for(i = 0;i < m;++i) 27 if(dis[edge[i].v] > dis[edge[j].u] + edge[j].w) 28 return false; 29 return true; 30 }
这个算法看看就好,时间复杂度太高了,下面是他的队列优化版,用下面的。
4)SPAF算法
还是别人家的博客好啊
https://www.cnblogs.com/jiangu66/p/3235361.html
https://blog.csdn.net/xunalove/article/details/70045815
其实 SPAF 算法是 Belleman-Ford算法的队列优化而已
就跟Belleman-Ford一样,用一个 dis 数组,然后将能松驰的边对应的终点加入队列,然后就出队入队了。我还是盗上博客二的吧
spfa的算法思想(动态逼近法):
设立一个先进先出的队列q用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。

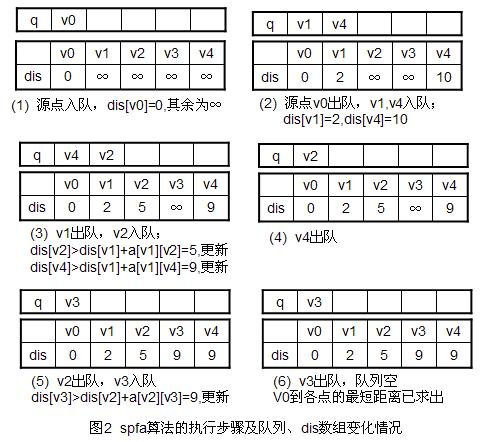
不过看很多人的模板使用数组模拟队列。。。。这就要注意数组的大小,据说在稀疏图中平均每个点进队不超过两次,可能开 2 * n 就够了吧??
SPAF算法判断负权回路:某点进队超过 n - 1 次!!!!
这个还是博客二的算法描述,当伪代码看(没有判断负权回路!!!!)
1 void spfa(s); //求单源点s到其它各顶点的最短距离 2 for i=1 to n do { dis[i]=∞; vis[i]=false; } //初始化每点到s的距离,不在队列 3 dis[s]=0; //将dis[源点]设为0 4 vis[s]=true; //源点s入队列 5 head=0; tail=1; q[tail]=s; //源点s入队, 头尾指针赋初值 6 while head<tail do { 7 head+1; //队首出队 8 v=q[head]; //队首结点v 9 vis[v]=false; //释放对v的标记,可以重新入队 10 for 每条边(v,i) //对于与队首v相连的每一条边 11 if (dis[i]>dis[v]+a[v][i]){ //如果不满足三角形性质 12 dis[i] = dis[v] + a[v][i] //松弛dis[i] 13 if (vis[i]=false) {tail+1; q[tail]=i; vis[i]=true;}} //不在队列,则加入队列(好像这里原博主少了大括号,现在以修正) 14 }
在实际应用的时候我习惯用链式前向星,下面关于链式前向星的构造,这东西我也是手动模拟数据才弄懂的,跟邻接表类似。
就用上面那个图做个链式前向星的测试操作吧,下面我的 head 组都初始化为 -1 , 我看很多人初始化为 0,看博的人注意点,别乱了。
1 struct Edge 2 { 3 int to, w, next; 4 }edge[MAXN]; 5 int head[MAXN], cnt; 6 7 void Add(int u, int v, int w) 8 { 9 edge[++cnt].to = v; 10 edge[cnt].w = w; 11 edge[cnt].next = head[u]; 12 head[u] = cnt; 13 } 14 15 void Search(int s) 16 { 17 cout << s; 18 for(int i = head[s];i != -1;i = edge[i].next) 19 cout << " -> " << edge[i].to; 20 cout << endl; 21 } 22 23 int main() 24 { 25 MemI(head); 26 int n, m; 27 cin >> n >> m; 28 int a, b, c; 29 for(int i = 0;i < m;++i) 30 { 31 cin >> a >> b >> c; 32 Add(a, b, c); 33 } 34 for(int i = 1;i <= n;++i) 35 Search(i); 36 return 0; 37 } 38 /* 39 5 7 40 1 2 2 41 1 5 10 42 2 5 7 43 2 3 3 44 5 3 6 45 4 5 5 46 3 4 4 47 */
给个SPAF算法的C++模板吧
struct Edge { int to, w, next; }edge[MAXN]; int head[MAXN], cnt; int n, dis[MAXN]; bool vis[MAXN]; queue<int> q; /*int book[MAXN];判断负权回路用, 板子没有就注释掉了*/ bool SPFA(int s) { memset(vis, 0, sizeof(vis)); // memset(book, 0, sizeof(book)); memset(dis, 0x3f, sizeof(dis)); while(!q.empty()) q.pop(); dis[s] = 0; vis[s] = true; // book[s]++; q.push(s); int v, i; while(!q.empty()) { v = q.front(); q.pop(); vis[v] = false; for(i = head[v];i != -1;i = edge[i].next) { if(dis[edge[i].to] > dis[v] + edge[i].w) { dis[edge[i].to] = dis[v] + edge[i].w; if(!vis[edge[i].to]) { // if(book[edge[i].to] >= n - 1) // return false; // book[edge[i].to]++; q.push(edge[i].to); } } } } return true; }
没找到合适的题啊!!!!随便找道水题吧。。。。模板题
HDU 2544 最短路
http://acm.hdu.edu.cn/showproblem.php?pid=2544
这里试试Bellman-Frod的模板过的

#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 10005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) struct Edge { int u, v, w; }edge[MAXN << 1]; int n, m, cnt, dis[105]; void Add(int a, int b, int c) { edge[++cnt].u = a; edge[cnt].v = b; edge[cnt].w = c; } bool BellmanFord(int s) { MemM(dis); dis[s] = 0; int i, j; for(i = 1;i < n;++i) for(j = 1;j <= m << 1;++j) if(dis[edge[j].v] > dis[edge[j].u] + edge[j].w) dis[edge[j].v] = dis[edge[j].u] + edge[j].w; for(j = 1;j <= m << 1;++j) if(dis[edge[j].v] > dis[edge[j].u] + edge[j].w) return false; return true; } int main() { while(cin >> n >> m) { cnt = 0; if(!n && !m) break; int a, b, c; for(int i = 0;i < m;++i) { cin >> a >> b >> c; Add(a, b, c); Add(b, a, c); } BellmanFord(1); cout << dis[n] << endl; } return 0; }
这里用SPAF 过的

#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 10005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) struct Edge { int to, w, next; }edge[MAXN << 1]; int head[MAXN << 1], cnt; int n, m, dis[MAXN]; bool vis[MAXN]; queue<int> q; /*int book[MAXN];判断负权回路用, 板子没有就注释掉了*/ void Add(int a, int b, int c) { edge[++cnt].to = b; edge[cnt].w = c; edge[cnt].next = head[a]; head[a] = cnt; } bool SPFA(int s) { memset(vis, 0, sizeof(vis)); // memset(book, 0, sizeof(book)); memset(dis, 0x3f, sizeof(dis)); while(!q.empty()) q.pop(); dis[s] = 0; vis[s] = true; // book[s]++; q.push(s); int v, i; while(!q.empty()) { v = q.front(); q.pop(); vis[v] = false; for(i = head[v];i != -1;i = edge[i].next) { if(dis[edge[i].to] > dis[v] + edge[i].w) { dis[edge[i].to] = dis[v] + edge[i].w; if(!vis[edge[i].to]) { // if(book[edge[i].to] >= n - 1) // return false; // book[edge[i].to]++; q.push(edge[i].to); } } } } return true; } int main() { while(cin >> n >> m) { cnt = 0; MemI(head); Mem0(edge); if(!n && !m) break; int a, b, c; while(m--) { cin >> a >> b >> c; Add(a, b, c); Add(b, a, c); } SPFA(1); cout << dis[n] << endl; } return 0; }
下面说优化方面的。。。。。
5)Dijkstra算法堆优化
如果图为稀疏图的话,即边数远小于 n^2,可以考虑用堆优化。主要是在取最小的边那个地方优化,个人习惯采用链式前向星存图,优先队列来模拟最小堆。
https://www.cnblogs.com/dancer16/p/6964454.html
用优先队列,直接上模板题题解
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 10005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) struct Edge { int to, w, next; }edge[MAXN << 1]; int head[MAXN], cnt; int dis[MAXN], n, m; //出队是最小的 struct cmp { bool operator () (const int a, const int b) { return dis[a] > dis[b]; } }; priority_queue<int, vector<int>, cmp> q; //好像SPAF啊 void Dijkstra(int s) { while(!q.empty()) q.pop(); memset(dis, 0x3f, sizeof(dis)); dis[s] = 0; q.push(s); int u; //理论上用Dijkstra的题不存在负权边,即每次选出来的边即为最短边, //所以每个点不可能被多次松弛,入队最多一次 //所以那个 vis 应该也是多余的 while(!q.empty()) { u = q.top(); q.pop(); for(int i = head[u];i != -1;i = edge[i].next) { if(dis[edge[i].to] > dis[u] + edge[i].w) { dis[edge[i].to] = dis[u] + edge[i].w; q.push(edge[i].to); } } } } void Add(int a, int b, int c) { edge[++cnt].to = b; edge[cnt].w = c; edge[cnt].next = head[a]; head[a] = cnt; } int main() { while(cin >> n >> m) { MemI(head); cnt = 0; if(!n && !m) break; int a, b, c; for(int i = 0;i < m;++i) { cin >> a >> b >> c; Add(a, b, c); Add(b, a, c); } Dijkstra(1); cout << dis[n] << endl; } return 0; }
6)SPFA算法两种优化(SLF,LLL)
https://blog.csdn.net/liangzhaoyang1/article/details/62423135
SLF:Small Label First 策略,设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,否则插入队尾。
LLL:Large Label Last 策略,设队首元素为i,队列中所有dist值的平均值为x,若dist(i)>x则将i插入到队尾,查找下一元素,直到找到某一i使得dist(i)<=x,则将i出对进行松弛操作。 SLF 可使速度提高 15 ~ 20%;SLF + LLL 可提高约 50%。 在实际的应用中SPFA的算法时间效率不是很稳定,为了避免最坏情况的出现,通常使用效率更加稳定的Dijkstra算法。
双端队列插入头尾的操作而已
