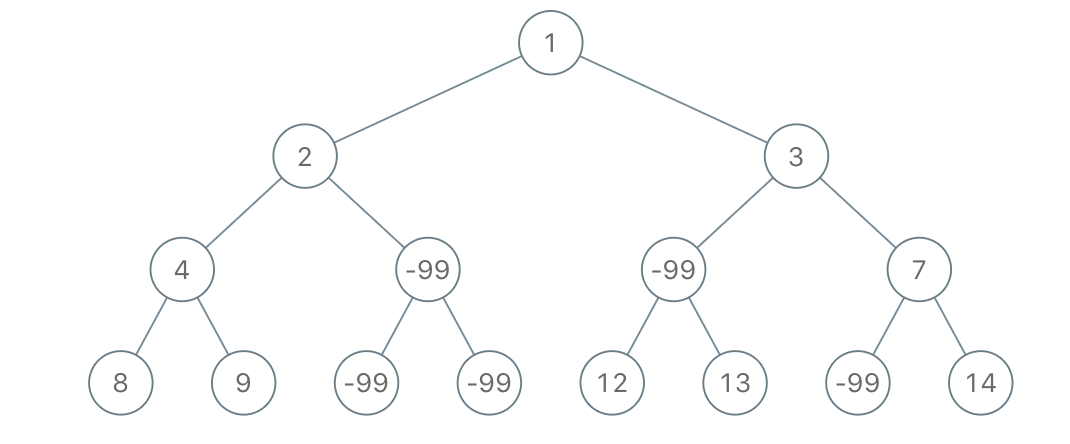
题目如下:
Given the
rootof a binary tree, consider all root to leaf paths: paths from the root to any leaf. (A leaf is a node with no children.)A
nodeis insufficient if every such root to leaf path intersecting thisnodehas sum strictly less thanlimit.Delete all insufficient nodes simultaneously, and return the root of the resulting binary tree.
Example 1:
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1Output: [1,2,3,4,null,null,7,8,9,null,14]
Example 2:
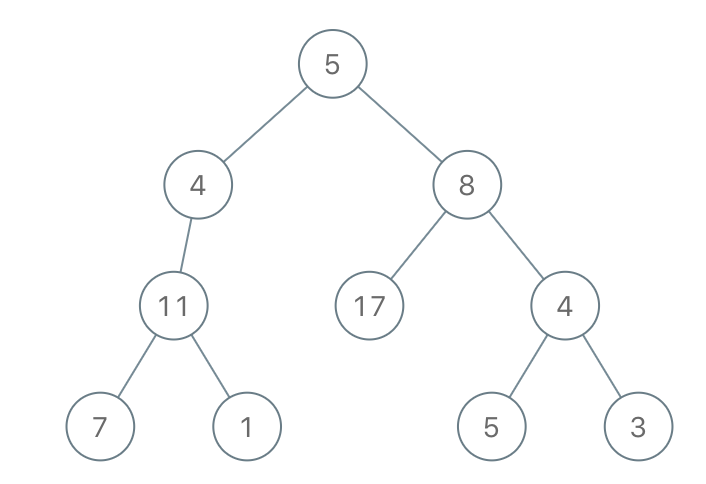
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22Output: [5,4,8,11,null,17,4,7,null,null,null,5]
Example 3:
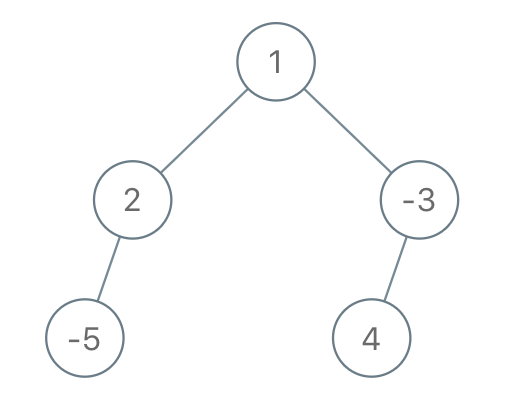 Input: root = [1,2,-3,-5,null,4,null], limit = -1
Input: root = [1,2,-3,-5,null,4,null], limit = -1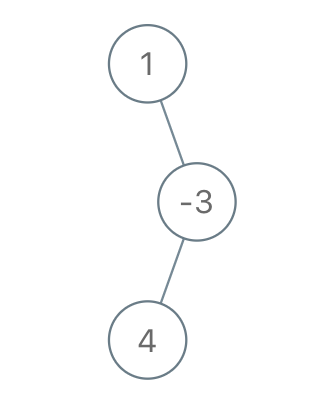 Output: [1,null,-3,4]
Output: [1,null,-3,4]Note:
- The given tree will have between
1and5000nodes.-10^5 <= node.val <= 10^5-10^9 <= limit <= 10^9
解题思路:我的方法是两次递归,第一次递归求出每个节点所对应路径的最大值并存储在字典中,第二次递归是删除最大值小于limit的节点以及其子树。
代码如下:
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): dic = {} def calculate(self,node,number,amount): if node.left == None and node.right == None: self.dic[number] = node.val + amount return node.val + amount left_v = -float('inf') right_v = -float('inf') if node.left != None: left_v = self.calculate(node.left,number*2,node.val + amount) if node.right != None: right_v = self.calculate(node.right,number*2+1,node.val + amount) #node.val = max(node.val,left_v,right_v) self.dic[number] = max(left_v,right_v) return self.dic[number] def recursive(self,node,number,limit): if node.left != None : if self.dic[number*2] >= limit: self.recursive(node.left,number*2,limit) else: node.left = None if node.right != None : if self.dic[number*2+1] >= limit: self.recursive(node.right,number*2+1, limit) else: node.right = None def sufficientSubset(self, root, limit): """ :type root: TreeNode :type limit: int :rtype: TreeNode """ self.dic = {} self.calculate(root,1,0) #print self.dic if self.dic[1] < limit: return None self.recursive(root,1,limit) return root