(mathcal{Description})
Link.(几乎一致)
给定 (n) 个点 (m) 条边的仙人掌和起点 (s),边长度均为 (1)。令 (d(u)) 表示 (u) 到 (s) 的最短距离。对于任意一个结点的排列 ({p_1,p_2,cdots,p_n}),记 (t_i) 满足 (p_{t_i}=i),称排列合法,当且仅当:
[(forall(u,v)in E)left((d(u)<d(v)
ightarrow t_u<t_v)land(d(u)>d(v)
ightarrow t_u>t_v)
ight)
]
求合法排列数,对 (998244353) 取模。
(nle10^4),(mle2 imes10^4),保证不存在 ((u,v)in E),使得 (d(u)=d(v))。
(mathcal{Solution})
考虑一个偶环(题目保证无奇环),起点终点在左右两端,上下各有 (l) 个结点相连。可见上下的点间是互不影响的,我们只需要分别保证上方和下方结点的相对位置。
再考虑一棵树,每个结点必须先于其子树内的点出现,所有方案为 (n!),每个结点 (u) 就会使其 ( imesfrac{1}{siz_u})。
对于仙人掌,处理出一棵 BFS 树,并得到环的信息。对于非环上的点,直接按树上的点来贡献系数。否则,对于一个环,如图:
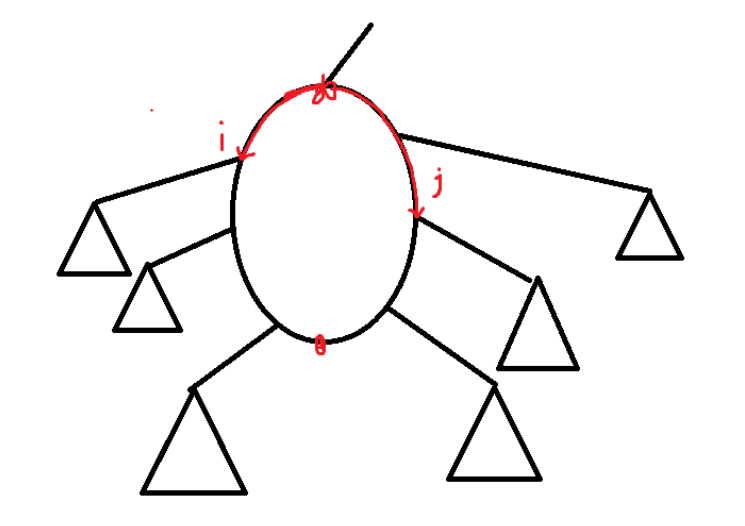
DP 求解,当前子树顺序已确定,令 (f(i,j)) 表示用左边前 (i) 个和右边前 (j) 个时对答案贡献的系数。转移比较显:
[f(i,j)=frac{1}{siz_i+siz_j}(f(i-1,j)+f(i,j-1))
]
其中 (siz_i) 表示 (i) 在 BFS 树上的子树大小,需要特殊处理 (i=0) 或 (j=0) 的情况。
(mathcal{Code})
#include <queue>
#include <cstdio>
#include <vector>
typedef std::pair<int, int> pii;
const int MAXN = 1e4, MAXM = 2e4, MOD = 998244353;
int n, m, s, ecnt = 1, inv[MAXN + 5], head[MAXN + 5], dist[MAXN + 5];
int fa[MAXN + 5], siz[MAXN + 5], sL[MAXN + 5], sR[MAXN + 5], f[MAXN + 5][MAXN + 5];
bool cut[MAXM + 5], vis[MAXN + 5];
std::vector<pii> cir;
struct Edge { int to, nxt; } graph[MAXM * 2 + 5];
inline void link ( const int s, const int t ) {
graph[++ ecnt] = { t, head[s] };
head[s] = ecnt;
}
inline void initBFTree () {
std::queue<int> que;
que.push ( s ), dist[s] = 1;
while ( !que.empty () ) {
int u = que.front (); que.pop ();
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( !dist[v = graph[i].to] ) {
fa[v] = u, dist[v] = dist[u] + 1;
que.push ( v );
} else if ( dist[v] > dist[u] ) {
cut[i >> 1] = true;
cir.push_back ( pii ( u, v ) );
}
}
}
}
inline void initSize ( const int u ) {
siz[u] = 1;
for ( int i = head[u], v; i; i = graph[i].nxt ) {
if ( !cut[i >> 1] && ( v = graph[i].to ) ^ fa[u] ) {
initSize ( v ), siz[u] += siz[v];
}
}
}
int main () {
freopen ( "abgfriend.in", "r", stdin );
freopen ( "abgfriend.out", "w", stdout );
scanf ( "%d %d %d", &n, &m, &s );
int ans = inv[1] = 1;
for ( int i = 2; i <= n; ++ i ) {
ans = 1ll * i * ans % MOD;
inv[i] = 1ll * ( MOD - MOD / i ) * inv[MOD % i] % MOD;
}
for ( int i = 1, u, v; i <= m; ++ i ) {
scanf ( "%d %d", &u, &v );
link ( u, v ), link ( v, u );
}
initBFTree ();
initSize ( s );
for ( int i = 0; i ^ cir.size (); ++ i ) {
int u = cir[i].first, v = cir[i].second, cnt = 0;
for ( int p = u, q = fa[v]; p ^ q; p = fa[p], q = fa[q] ) {
vis[p] = vis[q] = true, ++ cnt;
sL[cnt] = siz[p], sR[cnt] = siz[q];
}
for ( int i = 0; i <= cnt; ++ i ) {
for ( int j = 0; j <= cnt; ++ j ) {
if ( !i && !j ) f[i][j] = 1;
else if ( !i ) f[i][j] = 1ll * f[i][j - 1] * inv[sR[j]] % MOD;
else if ( !j ) f[i][j] = 1ll * f[i - 1][j] * inv[sL[i] + siz[v]] % MOD;
else f[i][j] = 1ll * ( f[i - 1][j] + f[i][j - 1] ) * inv[sL[i] + sR[j]] % MOD;
}
}
ans = 1ll * ans * f[cnt][cnt] % MOD;
}
for ( int i = 1; i <= n; ++ i ) {
if ( !vis[i] ) {
ans = 1ll * ans * inv[siz[i]] % MOD;
}
}
printf ( "%d
", ans );
return 0;
}
(mathcal{Details})
一开始局部变量 cnt 没赋初值,Windows 贴心地帮助兔子清了零,然后在 Lemon 上测 RE 一大片 qwq……