听说有人要计算♂几何的模板和专题，@S.G.G，所以就先写了一个计算几何的专题blog。
概述：
我们首先加入这样的结构体模板：Point,Line，分别代表点和边.
Point:
1 struct Point { // 二维点或矢量 2 double x, y; 3 double angle, dis; 4 Point() {} 5 Point(double x0, double y0): x(x0), y(y0) {} 6 };
Line:
1 struct Line { // 二维的直线或线段 2 Point p1, p2; 3 Line() {} 4 Line(Point p10, Point p20): p1(p10), p2(p20) {} 5 };
定义完这两个基本类型，我们就可以开始做计算几何的大部分题目了！
1.点积
a·b = |a|*|b|*cosθ
由于cos的性质，当a与b角度大于90度时，点积为负数；
当a与b角度大于90度时，点积为正数；
当ab垂直时 ，点积为零 ；
（不满足交换律！）
应用1：
判定两个向量的垂直关系、同向反向关系。
应用2：
a·b/|b|=(|a|*|b|*cosθ)/(|b|)=|a|*cosθ 也就是a向量在b向量的投影
1 double operator /(Point p1,Point p2){return p1.x*p2.x+p1.y*p2.y;}
2.叉积
a×b=|a|*|b|*sinθ
(叉积同样不满足交换律！)
由于sin的性质，当a在b的逆时针方向时，叉积为负数；
a在b的顺时针方向时，叉积为正数；
当ab同向或者反向时 ，叉积为零 ；
应用1：
判定两个向量的顺逆关系.
应用2：
a×b=ab向量的有向面积，应用广泛，常常用于三角剖分，也用于旋转卡壳（qiao）求高
程序：
1 double operator *(Point p1,Point p2){return p1.x*p2.y-p1.y*p2.x;}
3.直线 线段相交
PS（我们通常将直线转换为ax+by+c=0或者y=kx+b）
3.1 线段是否相交的判定
a.快速排斥实验：
设以线段A1A2和线段B1B2为对角线的矩形为M,N;
若M,N 不相交，则两个线段显然不相交；
所以：满足第一个条件时：两个线段可能相交。
b.跨立实验：若两线段相交，则两线段必然相互跨立对方。若A1A2跨立B1B2，则矢量( A1 - B1 ) 和(A2-B1)位于矢量(B2-B1)的两侧。
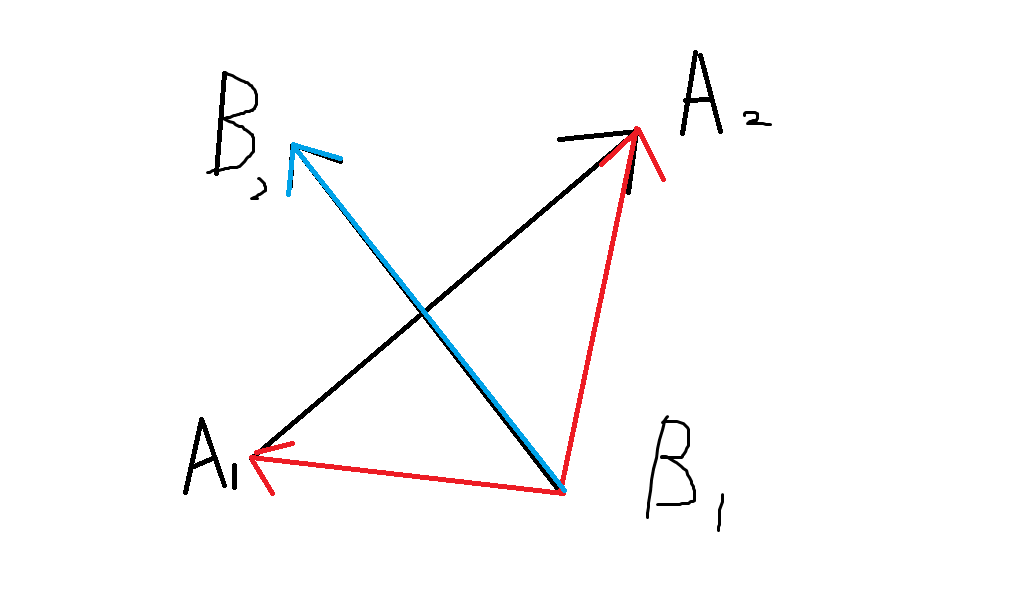
即(A1-B1) × (B2-B1) * (A2-B1) × (B2-B1)<0。
上式可改写成(A1-B1) × (B2-B1) * (B2-B1) × (A2-A1)>0。
应该判断两次，即两条线段都要为直线，判断另一直线的两端点是否在它两边，若是则两线段相交。
总体分析：
当(A1-B1) × (B2-B1)=0时，说明(A1-B1)和(B2-B1)共线，但是因为已经通过快速排斥试验，所以 A1一定在线段 B1B2上；同理，(B2-B1)×(A2-B1)=0 说明A2一定在线段B1B2上。所以判断A1A2跨立B1B2的依据是：(A1-B1) × (B2-B1) * (B2-B1) × (A2-B1) >= 0。
同理判断B1B2跨立A1A2的依据是：(B1-A1) × (A2-A1) * (A2-A1) × (B2-A1) >= 0。
注意:如果题目要求直线与线段相交:若直线为l1,线段为l2，那么只要判断线段是不是在直线的左右即可，
例如图中，只要判断（(e2s1)X(e2e1)）*（(s2s1)X(s2e1)）<=0即可，因为这种判断只能判断是否在另一条的直线上而无法判断是否在线段上，而判断线段相交需要上述的快速排斥和跨立实验。
3.2 线段相交的点
若两线段相交，则两线段所代表直线相交，直线交点即是线段交点（请跳转3.4)
3.3 直线求交判定
判定y=kx+b中k是否相同，或者ax+by+c=0中b/a是否相同
（你tm在逗我吗？同一平面直线如果不是平行那么肯定相交啊）
3.4 直线求交点
套公式，直接上代码：（ax+by+c=0公式）
1 Point Intersection(Point p1,Point p2,Point p3,Point p4){//求两相交线段交点 2 double a1=p1.y-p2.y; 3 double b1=p2.x-p1.x; 4 double c1=p1.x*p2.y-p1.y*p2.x; 5 double a2=p3.y-p4.y; 6 double b2=p4.x-p3.x; 7 double c2=p3.x*p4.y-p3.y*p4.x; 8 double x=(b1*c2-b2*c1)/(a1*b2-a2*b1); 9 double y=(a2*c1-a1*c2)/(a1*b2-a2*b1); 10 return Point(x,y); 11 }
注意，ax+by+c=0只有2个方程组成的方程组有无数组解，因此我们先让a=y1-y2,然后b和c就可以推出来了！
（y=kx+b公式）
1 Point inter(Line l1,Line l2){ 2 double y=(l1.b*l2.k-l2.b*l1.k)/(l2.k-l1.k); 3 double x=(y-l1.b)/(l1.k); 4 return Point(x,y); 5 }
4.凸包Graham算法
凸包有很多重要性质，若从一个顶点出发，那么边的方向是"单调不降"的：若我从点出发逆时针绕凸包走，所经过的边也是逆时针旋转的。
Graham步骤:
(1) 找出“最小”的点：
y坐标最小为第一关键字，x坐标最小为第二关键字。
1 bool operator <(Point p1,Point p2){ 2 if (fabs(p1.y-p2.y)<eps) return p1.x<p2.x; 3 return p1.y<p2.y; 4 }
1 for (int i=2;i<=n;i++) if (p[i]<p[1]) std::swap(p[i],p[1]);
（2）将这个“最小点”放到1的位置，对2到n的点极角排序
1 bool cmp(Point p1,Point p2){ 2 double t=(p1-p[1])*(p2-p[1]); 3 if (fabs(t)<eps) return dis(p1-p[1])-dis(p2-p[1])<0; 4 return t>0; 5 }
（3）用栈维护，如果要加入新的边会出现“凹包”，那么将栈顶元素弹出，然后再加入
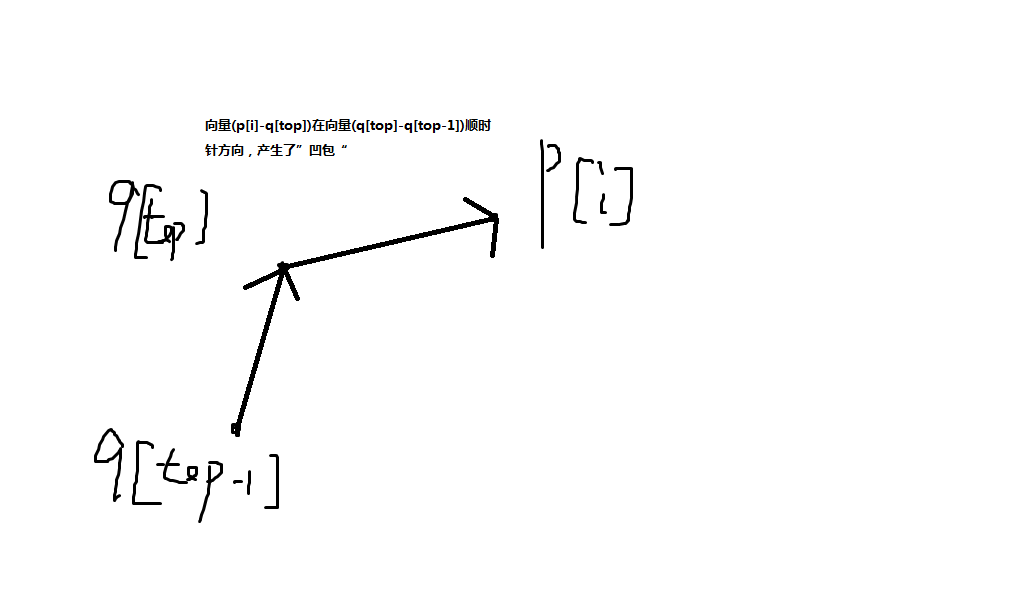代码：
1 int top=1; 2 q[1]=p[1]; 3 for (int i=2;i<=num;i++){ 4 while (top>1&&(q[top]-q[top-1])*(p[i]-q[top])<=0) top--; 5 q[++top]=p[i]; 6 }
(4).q（栈）存着的元素就是凸包上的点辣（已经按逆时针顺序排好了）
5.旋转卡（qia）壳（qiao）
这是对于凸包进行的算法，有很多做法，都统称旋转卡（qia）壳（qiao）
例如对于一个凸包，我们要求它的最小覆盖矩形！
那么我们会发现：如果有最小矩形存在，那么一定有一条矩形边和凸包边贴合
证明：如果没有边和凸包边相贴，一定可以通过旋转找到相同大小或者更小的矩形和凸包贴合。
步骤如下：
（1）构造凸包
（2）构造三个指针，分别代表“左”，“上”，“右”
（3）逆时针枚举边，对于每个边，都能找到“左”，“上”，“右”
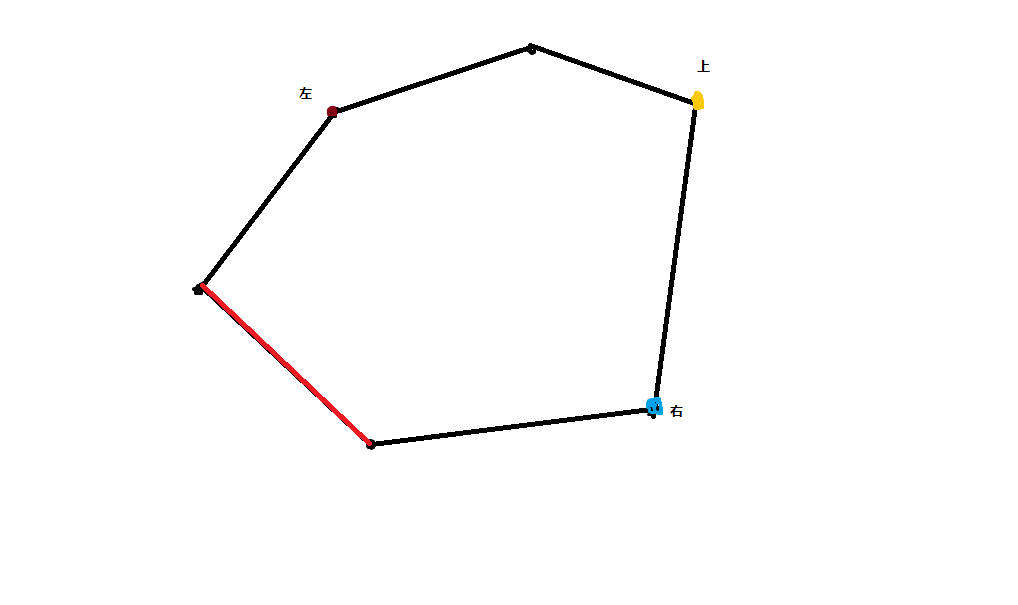
这时就要用到我们上面讲到的叉积点积的有向面积和投影了。
我们将“左”“上”“右”的点用L、H、R代表
求L：如果L+1在(q[i],q[i+1])的投影比L在(q[i],q[i+1])的投影小，(由于反向，所以点积越小越左边）
那么L=（L+1)%top
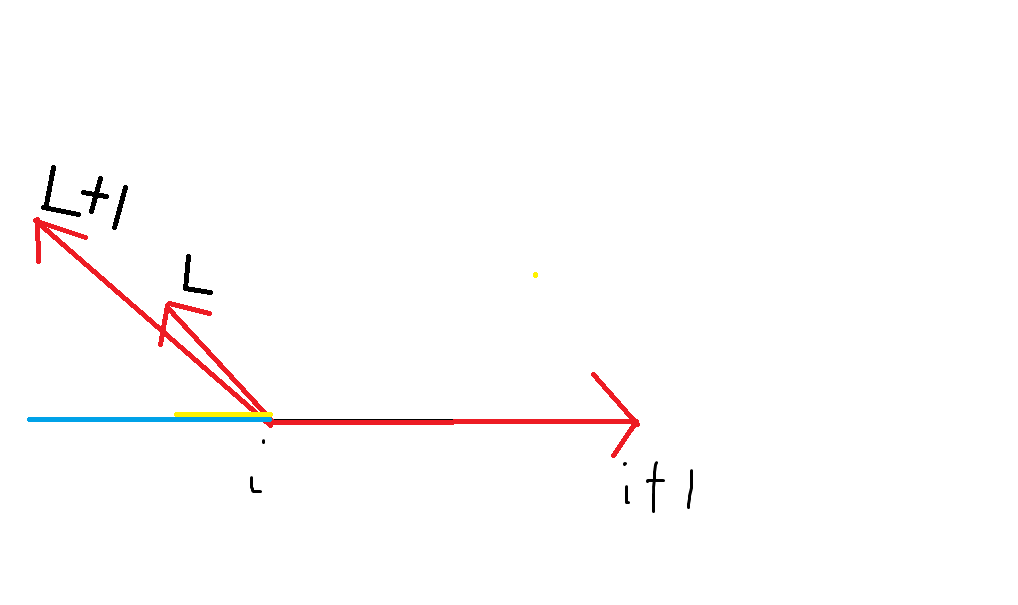求R：同理，如果R+1在q[i],q[i+1]投影大于R的投影，那么R=（R+1）%top
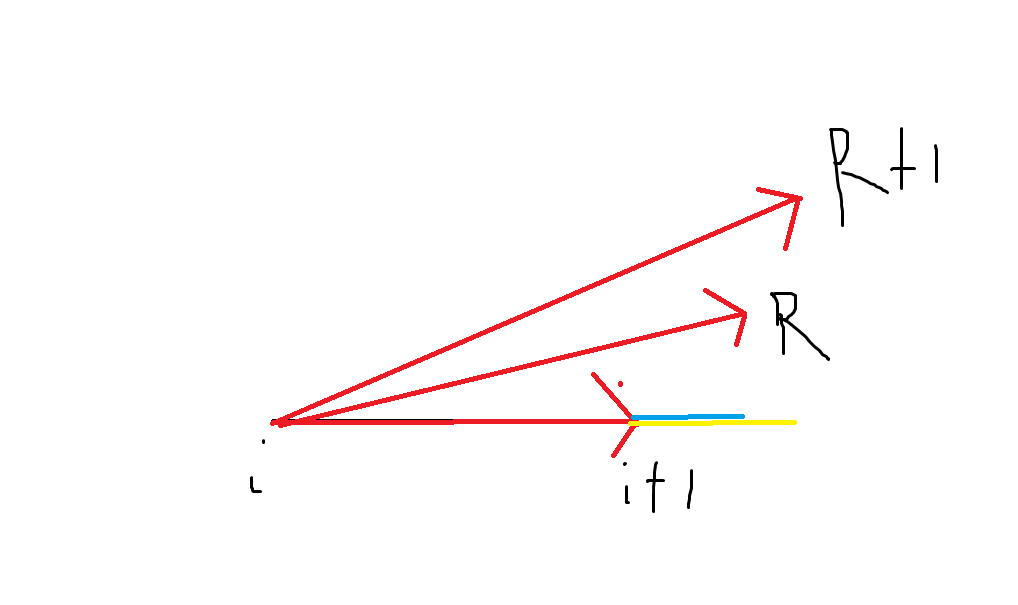
然后求H：
如果（H+1）与（q[i],q[i+1])的面积绝对值大于(H）与（q[i],q[i+1])的面积绝对值
那么H=（H+1）%top（由于底不变，高越大，面积也越大）
所以求出L,R,H以后，面积就能求了，这个面积与答案比较，如果比答案小，那么答案就赋值为这个面积。
时间复杂度？由于枚举是O（n)的，L、R、H的旋转随着枚举而旋转，旋转也是O（n）的，所以总复杂度是构造凸包：O（nlogn）
例题：bzoj1185
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<string> 6 #include<algorithm> 7 double eps=1e-8,ans; 8 int n,top; 9 struct Point{ 10 double x,y; 11 Point(){} 12 Point(double x0,double y0):x(x0),y(y0){} 13 }p[200005],q[200005],t[5]; 14 double operator *(Point p1,Point p2){ 15 return p1.x*p2.y-p2.x*p1.y; 16 } 17 Point operator -(Point p1,Point p2){ 18 return Point(p1.x-p2.x,p1.y-p2.y); 19 } 20 Point operator /(Point p1,double x){ 21 return Point(p1.x/x,p1.y/x); 22 } 23 Point operator +(Point p1,Point p2){ 24 return Point(p1.x+p2.x,p1.y+p2.y); 25 } 26 Point operator *(Point p1,double x){ 27 return Point(p1.x*x,p1.y*x); 28 } 29 double dis(Point p){ 30 return sqrt(p.x*p.x+p.y*p.y); 31 } 32 bool operator <(Point p1,Point p2){ 33 if (fabs(p1.y-p2.y)<eps) return p1.x<p2.x; 34 return p1.y<p2.y; 35 } 36 double operator /(Point p1,Point p2){ 37 return p1.x*p2.x+p1.y*p2.y; 38 } 39 bool operator >(Point p1,Point p2){ 40 if (fabs(p1.y-p2.y)<eps) return p1.x>p2.x; 41 return p1.y>p2.y; 42 } 43 bool cmp(Point p1,Point p2){ 44 double t=(p1-p[1])*(p2-p[1]); 45 if (fabs(t)<eps) return dis(p1-p[1])-dis(p2-p[1])<0; 46 return t>0; 47 } 48 void graham(){ 49 for (int i=2;i<=n;i++) if (p[i]<p[1]) std::swap(p[i],p[1]); 50 std::sort(p+2,p+1+n,cmp); 51 int L=1; 52 q[1]=p[1]; 53 for (int i=2;i<=n;i++){ 54 while (L>1&&(q[L]-q[L-1])*(p[i]-q[L])<eps) L--; 55 q[++L]=p[i]; 56 } 57 q[0]=q[L]; 58 top=L; 59 } 60 void Rotating_Calipers(){ 61 int l=1,r=1,p=1; 62 double D,L,R,H; 63 for (int i=0;i<top;i++){ 64 D=dis(q[i]-q[i+1]); 65 while ((q[i+1]-q[i])*(q[p+1]-q[i])-(q[i+1]-q[i])*(q[p]-q[i])>-eps) p=(p+1)%top; 66 while ((q[i+1]-q[i])/(q[r+1]-q[i])-(q[i+1]-q[i])/(q[r]-q[i])>-eps) r=(r+1)%top; 67 if (i==0) l=r; 68 while ((q[i+1]-q[i])/(q[l+1]-q[i])-(q[i+1]-q[i])/(q[l]-q[i])<eps) l=(l+1)%top; 69 L=(q[i+1]-q[i])/(q[l]-q[i])/D; 70 R=(q[i+1]-q[i])/(q[r]-q[i])/D; 71 H=(q[i+1]-q[i])*(q[p]-q[i])/D; 72 if (H<0) H=-H; 73 double tmp=H*(R-L); 74 if (tmp<ans){ 75 ans=tmp; 76 t[0]=q[i]+(q[i+1]-q[i])/D*R; 77 t[1]=t[0]+(q[r]-t[0])*(H/dis(t[0]-q[r])); 78 t[2]=t[1]-(t[0]-q[i])*((R-L)/dis(q[i]-t[0])); 79 t[3]=t[2]+t[0]-t[1]; 80 } 81 } 82 } 83 int main(){ 84 freopen("tx.in","r",stdin); 85 scanf("%d",&n); 86 for (int i=1;i<=n;i++) 87 scanf("%lf%lf",&p[i].x,&p[i].y); 88 graham(); 89 ans=1e60; 90 Rotating_Calipers(); 91 printf("%.5f ",ans); 92 int be=0; 93 for (int i=1;i<=3;i++){ 94 if (t[i]<t[be]) be=i; 95 } 96 for (int i=0;i<=3;i++) 97 printf("%.5f %.5f ",t[(i+be)%4].x,t[(i+be)%4].y); 98 }
6.半平面交
通常是处理 多边形的核 或者是 二元一次不等式组的 求解，也就是线性规划的求解，解是凸包，且求出来的解的点已经按照 逆时针/顺时针 排好序了。
至于步骤：首先建立所有的直线，并且规定好方向：
方向是什么概念？
假如我们有一个凸包，凸包上面的直线所表示区域全部朝向凸包内侧，那么我们可以规定沿着这个凸包的边缘，所有直线的a向b均是“逆时针”。
规定完方向以后，我们就可以 半♂平♂面♂交 了！
先将边的“斜率”规定为atan2(l.b.y-l.a.y,l.b.x-l.a.x)
并以斜率为关键字从小到大排序，如果有斜率相同的，当然是“有用”的直线留在后面（这与我们的写法有关）
然后我们维护一个队列，如果队尾的两个直线交点不在直线所表示范围内，那么队尾弹出。
如果队头的两个直线交点不在直线所表示范围内，那么队头弹出。
注意一定要先判断队尾再判断队头，也就是先判断R那端然后判断L那端。
然后扫完的最后还是要再判断一次。
最终在队列中L到R的这部分直线便是核的凸包的边，这些相邻边的交点就是核的凸包上面的点。
交个例题：bzoj1038
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstdio> 6 struct Point{ 7 double x,y; 8 Point(){} 9 Point(double x0,double y0):x(x0),y(y0){} 10 }p[100005],a[200005]; 11 struct Line{ 12 Point a,b; 13 double slop; 14 Line(){} 15 Line(Point a0,Point b0):a(a0),b(b0){} 16 }l[200005],q[200005]; 17 int n,cnt,tot; 18 int read(){ 19 char ch=getchar();int t=0,f=1; 20 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 21 while ('0'<=ch&&ch<='9'){t=t*10+ch-'0';ch=getchar();} 22 return t*f; 23 } 24 double operator *(Point p1,Point p2){ 25 return p1.x*p2.y-p1.y*p2.x; 26 } 27 Point operator -(Point p1,Point p2){ 28 return Point(p1.x-p2.x,p1.y-p2.y); 29 } 30 bool cmp(Line p1,Line p2){ 31 if (p1.slop!=p2.slop) return p1.slop<p2.slop; 32 else return (p1.b-p1.a)*(p2.b-p1.a)>0; 33 } 34 Point inter(Line p1,Line p2){ 35 double t1=(p2.b-p1.a)*(p1.b-p1.a); 36 double t2=(p1.b-p1.a)*(p2.a-p1.a); 37 double k=t1/(t1+t2); 38 Point p; 39 p.x=p2.b.x+(p2.a.x-p2.b.x)*k; 40 p.y=p2.b.y+(p2.a.y-p2.b.y)*k; 41 return p; 42 } 43 bool jud(Line p1,Line p2,Line p3){ 44 Point p=inter(p1,p2); 45 return (p3.b-p3.a)*(p-p3.a)<0; 46 } 47 void prework(){ 48 p[0].x=p[1].x;p[0].y=100005; 49 p[n+1].x=p[n].x;p[n+1].y=100005; 50 for (int i=1;i<=n;i++){ 51 l[++cnt].a=p[i-1];l[cnt].b=p[i]; 52 l[++cnt].a=p[i];l[cnt].b=p[i+1]; 53 } 54 for (int i=1;i<=cnt;i++) l[i].slop=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x); 55 std::sort(l+1,l+1+cnt,cmp); 56 } 57 void hpi(){ 58 int L=1,R=0;tot=0; 59 for (int i=1;i<=cnt;i++){ 60 if (l[i].slop!=l[i-1].slop) tot++; 61 l[tot]=l[i]; 62 } 63 cnt=tot; 64 q[++R]=l[1];q[++R]=l[2]; 65 for (int i=3;i<=cnt;i++){ 66 while (L<R&&jud(q[R],q[R-1],l[i])) R--; 67 while (L<R&&jud(q[L],q[L+1],l[i])) L++; 68 q[++R]=l[i]; 69 } 70 while (L<R&&jud(q[R],q[R-1],q[L])) R--; 71 while (L<R&&jud(q[L],q[L+1],q[R])) L++; 72 tot=0; 73 for (int i=L;i<R;i++) 74 a[++tot]=inter(q[i],q[i+1]); 75 76 } 77 void getans(){ 78 double ans=1e60; 79 for (int k=1;k<=tot;k++) 80 for (int i=1;i<n;i++){ 81 Point t;t.x=a[k].x;t.y=-1; 82 if (p[i].x<=a[k].x&&a[k].x<=p[i+1].x) ans=std::min(ans,a[k].y-inter(Line(p[i],p[i+1]),Line(a[k],t)).y); 83 } 84 for (int k=1;k<=n;k++) 85 for (int i=1;i<tot;i++){ 86 Point t;t.x=p[k].x;t.y=-1; 87 if (a[i].x<=p[k].x&&p[k].x<=a[i+1].x) ans=std::min(ans,inter(Line(a[i],a[i+1]),Line(p[k],t)).y-p[k].y); 88 } 89 printf("%.3lf",ans); 90 } 91 int main(){ 92 //freopen("bzoj1038.in","r",stdin); 93 //freopen("bzoj1038.out","w",stdout); 94 scanf("%d",&n); 95 for (int i=1;i<=n;i++) p[i].x=read(); 96 for (int i=1;i<=n;i++) p[i].y=read(); 97 prework(); 98 hpi(); 99 getans(); 100 }
7.三角剖♂分
我们通常用三角剖分来处理圆和简单多边形的相交面积。
我们考虑到，我们计算多边形面积，最经常用的就是把多边形剖分，变成很多个有向三角形的面积！
考虑到这里，我们把问题转变成了很多个有向三角形和圆的面积交。
三角形和圆的面积交，有以下几种情况：
（1）:三角形两边都小于r
此时直接返回三角形的有效面积即可。
(2)三角形两边都大于R，且第三条边到圆心的距离大于R
此时返回这个覆盖的扇形面积
(3)两边都大于R，但第三边到圆心距离小于R，且顶上两个角都是锐角(可以有一个直角)
这样就变成2个三角形和一个扇形的面积了。
(3)两边都大于R，且距离小于R，且顶上两个角有一个是钝角。
这样还是一个扇形的面积。
(4)有一边大于R，一边小于R
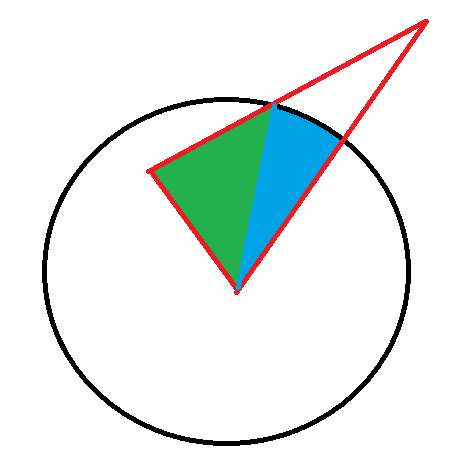
这样就是一个扇形和一个三角形的面积
注意计算完面积要记得乘以这个三角形的有向符号(-1或1)
模板:POJ3675
1 #include<algorithm> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<iostream> 6 struct Point{ 7 double x,y; 8 Point(){} 9 Point(double x0,double y0):x(x0),y(y0){} 10 }p[200005],a[5],O; 11 struct Line{ 12 Point s,e; 13 Line(){} 14 Line(Point s0,Point e0):s(s0),e(e0){} 15 }; 16 int n; 17 double R; 18 const double eps=1e-8; 19 const double Pi=acos(-1); 20 double sgn(double x){ 21 if (x>eps) return 1.0; 22 if (x<-eps) return -1.0; 23 return 0; 24 } 25 Point operator *(Point p1,double x){ 26 return Point(p1.x*x,p1.y*x); 27 } 28 Point operator /(Point p1,double x){ 29 return Point(p1.x/x,p1.y/x); 30 } 31 double operator /(Point p1,Point p2){ 32 return p1.x*p2.x+p1.y*p2.y; 33 } 34 double operator *(Point p1,Point p2){ 35 return p1.x*p2.y-p1.y*p2.x; 36 } 37 Point operator +(Point p1,Point p2){ 38 return Point(p1.x+p2.x,p1.y+p2.y); 39 } 40 Point operator -(Point p1,Point p2){ 41 return Point(p1.x-p2.x,p1.y-p2.y); 42 } 43 double dis(Point p1){ 44 return sqrt(p1.x*p1.x+p1.y*p1.y); 45 } 46 double dis(Point p1,Point p2){ 47 return dis(Point(p1.x-p2.x,p1.y-p2.y)); 48 } 49 double sqr(double x){ 50 return x*x; 51 } 52 double dist_line(Line p){ 53 double A,B,C,dist; 54 A=p.s.y-p.e.y; 55 B=p.s.x-p.e.x; 56 C=p.s.x*p.e.y-p.s.y*p.e.x; 57 dist=fabs(C)/sqrt(sqr(A)+sqr(B)); 58 return dist; 59 } 60 double get_cos(double a,double b,double c){ 61 return (b*b+c*c-a*a)/(2*b*c); 62 } 63 double get_angle(Point p1,Point p2){ 64 if (!sgn(dis(p1))||!sgn(dis(p2))) return 0.0; 65 double A,B,C; 66 A=dis(p1); 67 B=dis(p2); 68 C=dis(p1,p2); 69 if (C<=eps) return 0.0; 70 return acos(get_cos(C,A,B)); 71 } 72 Point get_point(Point p){ 73 double T=sqr(p.x)+sqr(p.y); 74 return Point(sgn(p.x)*sqrt(sqr(p.x)/T),sgn(p.y)*sqrt(sqr(p.y)/T)); 75 } 76 double S(Point p1,Point p2,Point p3){ 77 return fabs((p2-p1)*(p3-p1))/2; 78 } 79 double work(Point p1,Point p2){ 80 double f=sgn(p1*p2),res=0; 81 if (!sgn(f)||!sgn(dis(p1))||!sgn(dis(p2))) return 0.0; 82 double l=dist_line(Line(p1,p2)); 83 double a=dis(p1); 84 double b=dis(p2); 85 double c=dis(p1,p2); 86 if (a<=R&&b<=R){ 87 return fabs(p1*p2)/2.0*f; 88 } 89 if (a>=R&&b>=R&&l>=R){ 90 double ang=get_angle(p1,p2); 91 return fabs((ang/(2.0))*(R*R))*f; 92 } 93 if (a>=R&&b>=R&&l<=R&&(get_cos(a,b,c)<=0||get_cos(b,a,c)<=0)){ 94 double ang=get_angle(p1,p2); 95 return fabs((ang/(2.0))*(R*R))*f; 96 } 97 if (a>=R&&b>=R&&l<=R&&(get_cos(a,b,c)>0&&get_cos(b,a,c)>0)){ 98 double dist=dist_line(Line(p1,p2)); 99 double len=sqrt(sqr(R)-sqr(dist))*2.0; 100 double ang1=get_angle(p1,p2); 101 double cos2=get_cos(len,R,R); 102 res+=fabs(len*dist/2.0); 103 double ang2=ang1-acos(cos2); 104 res+=fabs((ang2/(2))*(R*R)); 105 return res*f; 106 } 107 if ((a>=R&&b<R)||(a<R&&b>=R)){ 108 if (b>a) std::swap(a,b),std::swap(p1,p2); 109 double T=sqr(p1.x-p2.x)+sqr(p1.y-p2.y); 110 Point u=Point(sgn(p1.x-p2.x)*sqrt(sqr(p1.x-p2.x)/T),sgn(p1.y-p2.y)*sqrt(sqr(p1.y-p2.y)/T)); 111 double dist=dist_line(Line(p1,p2)); 112 double len=sqrt(R*R-dist*dist); 113 double len2=sqrt(sqr(dis(p2))-sqr(dist)); 114 if (fabs(dis(p2+u*len2)-dist)<=eps) len+=len2; 115 else len-=len2; 116 Point p=p2+u*len; 117 res+=S(O,p2,p); 118 double ang=get_angle(p1,p); 119 res+=fabs((ang/2.0)*R*R); 120 return res*f; 121 } 122 return 0; 123 } 124 int main(){ 125 O=Point(0,0); 126 while (scanf("%lf",&R)!=EOF){ 127 scanf("%d",&n); 128 for (int i=1;i<=n;i++) 129 scanf("%lf%lf",&p[i].x,&p[i].y); 130 p[n+1]=p[1]; 131 double ans=0; 132 for (int i=1;i<=n;i++) 133 ans+=work(p[i],p[i+1]); 134 ans=fabs(ans); 135 printf("%.2f ",ans); 136 } 137 }