Description
银河历59451年,在银河系有许许多多已被人类殖民的星系。如果想要在行
星系间往来,大家一般使用连接两个行星系的跳跃星门。 一个跳跃星门可以把
物质在它所连接的两个行星系中互相传送。
露露、花花和萱萱被银河系星际联盟调查局任命调查商业巨擘ZeusLeague+
的不正当商业行为。
在银河系有N个已被ZeusLeague+成功打入市场的行星系,不妨标号为
1,2,...,N。而ZeusLeague+在这N个行星系之间还拥有自己的M个跳跃星门。使
用这些跳跃星门,ZeusLeague+的物资就可以在这N个行星系中两两任意互相传
输。由于经费问题,跳跃星门的个数不会超过行星系的个数。
露露在颇费周折之后得到了ZeusLeague+在这N个行星系中的各自的贸易总
额C[i]。
萱萱设计了一个经济学特征指标D[i]来度量这N个行星系的经济学特征。于
是,我们可以用二元组(C[i],D[i])来表示第i个行星系的XP(Xuan's Position)。现
在假设我们有k个行星系的XPs,把它们放置在二维平面上,然后我们用一条直
线去拟合这些XPs。定义一条直线与XPs的相斥度为这条直线到各个XP的Euclid
距离的平方之和。再令XPs的线性假设相斥度为所有直线与XPs的相斥度中的
最小者。那么,这个值越小,ZeusLeague+在这k个行星系中的相互贸易活动就
越可疑,从而值得进一步调查。花花负责计算许多行星系对(u,v)的非可疑度。一
条跳跃星门航线的非可疑度被定义为它经过的所有行星系(包括起点和终点)的
XPs的线性假设相斥度。而一个行星系对(u,v)的非可疑度则被定义为所有以u为
起点,v为终点的跳跃星门航线的非可疑度中的最小值。一条跳跃星门航线是指
从某个行星系开始,通过跳跃星门依次到达某些行星系,然后终止,并且中途不
重复经过行星系,这样的一个过程。
花花负责计算许多行星系对(u,v)的非可疑度。一条跳跃星门航线的非可疑度
被定义为它经过的所有行星系(包括起点和终点)的XPs的线性假设相斥度。
而一个行星系对(u,v)的非可疑度则被定义为所有以u为起点,v为终点的跳跃星
门航线的非可疑度中的最小值。一条跳跃星门航线是指从某个行星系开始,通过
跳跃星门依次到达某些行星系,然后终止,并且中途不重复经过行星系,这样的
一个过程。
在花花数天夜以继日的工作之后,平行调查组的你——大名鼎鼎的计算机科
学家Hcceleration.Gerk.Gounce不忍心看到她这样不眠不休,于是你在完成了手
头的工作之后决定帮一帮她。
Input
第一行是N,M,分别表示这个银河系内的行星系的个数
以及跳跃星门的个数。
接下来N行,每行2个正整数C[i], D[i],表示第i 个行星系的XP(Xuan's Position)。
接下来的M行来描述跳跃星门,每行2个正整数u[i],v[i],表示有一个连接
着行星系u[i]和v[i]的跳跃星门。注意这个连接是无向的。不会存在自己连向自
己的情况。也不会存在重复连接的情况。
接下来的一行,有一个正整数Q,表示花花需要计算的非可疑度的行星对数。
接下来的Q行,每行2个正整数s[i], t[i],表示花花需要计算从s[i]到t[i]的
非可疑度。
Output
总共Q行,每一行一个实数,表示花花第i次需要计算的答
案。你的答案需要和标准答案的差不超过0.01才能得分。
Sample Input
6 6
3 4
5 6
1 3
4 4
3 3
2 4
1 2
1 3
2 3
2 4
3 5
5 6
3
3 6
2 4
4 6
Sample Output
0.66667
0.00000
1.67544
一道良心的必修一压轴题+树链剖分
通过一系列漫长的推导+勇敢的展开,最后只需要维护
推导的话主要是运用两次主元法(点到直线距离公式要记得),最后由求根公式即可,推导以后补:
设最后的那条直线的解析式为y=kx+b,设n为路径上的点数
由点到直线的距离公式:
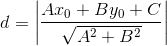
带入暴算并把b当做主元:
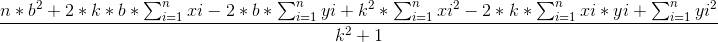
分子是一个二次函数形式,可以计算出整个式子取最小值时的b值(二次函数顶点)

令:
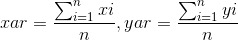
则 b=yar-xar;
在把b带入以k为主元:
可以把分子变为一个关于k的二次函数形式:
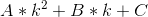
令:
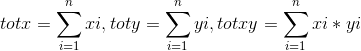
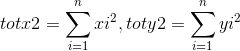
则 暴力计算可得到
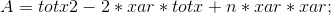
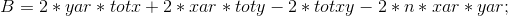
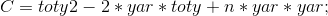
所以
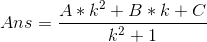
乘过去:
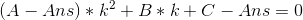
由于有解,所以
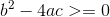
所以:
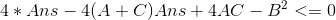
易知在Ans取较小的那个零点的时候为所求答案,由求根公式计算即可;
不容易啊
因为图连通且不超过n条边,所以为树或者一个基环树
树的话直接树链剖分,维护的东西直接用树上前缀和即可: x+y-lca-fa[lca];
基环树的话,把环看做根节点后就是树了,如果lca为环的话分别跳到环上,
环上的按照某种时针顺序预处理前缀和,然后分别走两条路统计即可.
如果lca不是环就正常树的即可
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define RG register
using namespace std;
const int N=300050;
int n,m,cnt,tot,root[N],head[N],to[N],nxt[N],fa[N],dep[N],size[N],son[N],top[N],cir[N],rt[N];
int tx[N],ty[N],vis[N];
int gi()
{
int x=0,flag=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') flag=-1;ch=getchar();}
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*flag;
}
struct data{
int pre[6];
void update(RG int u,RG int v){
pre[0]++;pre[1]+=u;pre[2]+=u*u;
pre[3]+=v;pre[4]+=v*v;pre[5]+=u*v;
}
double query(){
RG double n=pre[0],totx=pre[1],toty=pre[3],totx2=pre[2],toty2=pre[4],totxy=pre[5];
RG double xar=totx/n,yar=toty/n;
RG double a=totx2-2*xar*totx+n*xar*xar;
RG double b=2*yar*totx+2*xar*toty-2*totxy-2*n*xar*yar;
RG double c=toty2-2*yar*toty+n*yar*yar;
RG double A=4.0,B=-4*(a+c),C=4*a*c-b*b;
return (-B-sqrt(B*B-4*A*C))/2/A;
}
}a[N],b[N];
data operator +(data x,data y){
for(RG int i=0;i<6;i++) x.pre[i]+=y.pre[i]; return x;
}
data operator -(data x,data y){
for(RG int i=0;i<6;i++) x.pre[i]-=y.pre[i]; return x;
}
void lnk(RG int x,RG int y){
to[++tot]=y;nxt[tot]=head[x];head[x]=tot;
}
inline void dfs1(int x,int f){
vis[x]=1;size[x]=1;son[x]=0;rt[x]=f;
a[x]=a[fa[x]]; a[x].update(tx[x],ty[x]);
for(RG int i=head[x];i;i=nxt[i]){
RG int y=to[i];
if (!vis[y]&&y!=fa[x]){
dep[y]=dep[x]+1;fa[y]=x;
dfs1(y,f);size[x]+=size[y];
if(size[y]>size[son[x]]) son[x]=y;
}
}
}
inline void dfs2(RG int x,RG int f){
top[x]=f;
if(son[x]) dfs2(son[x],f);
for (RG int i=head[x]; i; i=nxt[i]){
RG int y=to[i];
if(x==fa[y] && y!=son[x]) dfs2(y,y);
}
}
inline int lca(RG int x,RG int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
return y;
}
inline void work(){
memset(vis,0,sizeof(vis));
for(RG int x=1;x<=n;x++)
for(RG int i=head[x];i;i=nxt[i]){
if(fa[x]!=to[i]&&fa[to[i]]!=x){
RG int y=to[i];
if(dep[x]>dep[y]) swap(x,y);
for(;y!=x;y=fa[y]){
root[++cnt]=y;cir[y]=cnt;vis[y]=1;
b[cnt]=b[cnt-1];b[cnt].update(tx[y],ty[y]);
}
root[++cnt]=x;cir[x]=cnt;vis[x]=1;
b[cnt]=b[cnt-1];b[cnt].update(tx[x],ty[x]);
return;
}
}
}
int main(){
n=gi(),m=gi();RG int x,y;
for(RG int i=1;i<=n;i++) tx[i]=gi(),ty[i]=gi();
for(RG int i=1;i<=m;i++){
x=gi(),y=gi();
lnk(x,y); lnk(y,x);
}
dfs1(1,1);
memset(vis,0,sizeof(vis));
if(n==m) work();else root[cnt=1]=1;
memset(fa,0,sizeof(fa));
for(RG int i=1;i<=cnt;i++){
dfs1(root[i],root[i]); dfs2(root[i],root[i]);
}
RG int Q=gi();data u,v;
for(RG int i=1;i<=Q;i++){
x=gi(),y=gi();
if (rt[x]==rt[y]){
u=a[x]+a[y]-a[lca(x,y)]-a[fa[lca(x,y)]];
printf("%.5f
",u.query());
} else{
if (cir[rt[x]]>cir[rt[y]]) swap(x,y);
u=a[x]-a[rt[x]]+a[y]-a[rt[y]]+b[cir[rt[y]]]-b[cir[rt[x]]-1];
v=a[x]-a[rt[x]]+a[y]-a[rt[y]]+b[cir[rt[x]]]+b[cnt]-b[cir[rt[y]]-1];
printf("%.5f
",min(u.query(),v.query()));
}
}
return 0;
}