运输计划
首先熟悉一下题目:
在一棵有边权的树(n个节点)上有m条路径,清零一条边的边权使得m条路径的最大值最小
至于数据范围
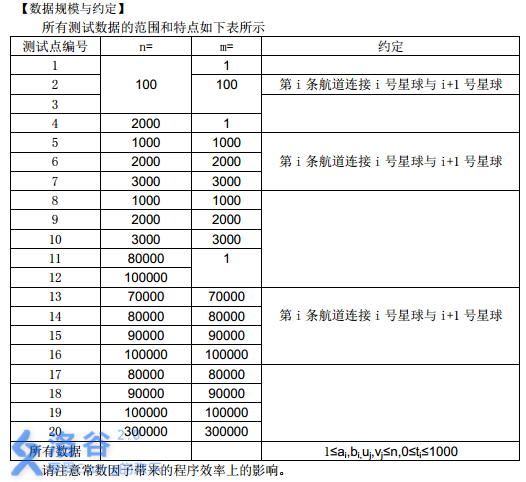
20分
m=1
好啦,好像可做,一眼望去全是水
只需求出一条链上的所有边并计算边权和及最大边权(暴力往上跳并记录即可)
边权和减去最大边权即为答案
那么我们就可以O(n)过掉这道题了(不嫌麻烦的话也可以O(log n)搞树上路径)
60分?
从未如此接近满分
全是链,这意味着什么(并不意味着什么)
想了想,发现好像60分并不好搞
考虑一下暴力吧
超级暴力:暴力枚举删每一条边,统计删完这条边之后最长链的长度,取最小值就是答案,复杂度O(n^2 m),25分
刚才的小优化
考虑优化暴力
枚举删哪条边O(n)显然已经达到理论下限
如果非要搞它的话只能排除那些不被经过的边,效率高不了多少
接下来是统计每条链的长度
全是链哎,求线性区间和,前缀和优化,消去一个O(n)
那个O(m)好像没有什么有效的优化
这样,复杂度降至O(nm),40分
然后其他数据,搞树链剖分动态修改、查询可以多拿一些分,复杂度O(nm log n),60分
怎么办
QAQ,60分都拿不到了吗
可不可以不实际改边权呢?
经过不会就猜二分
经过深入思考,我们发现:
最短时间为t,前提是对于length>t的所有链,总能找到至少一条长为k公共边,使得最长链的长度max length-k<=t
如果知道答案,好像不仅不用枚举最长链,还可以把枚举删边变为贪心删掉被全部满足条件的链经过的最长边,稳赚一个O(n)和一个O(m)
考虑二分答案
如果能够在时间t1内完成任务,那么对于t2>t1,总能在时间t2内完成任务
所以答案符合单调性
可以二分答案
Check函数怎么写呢,看一看能不能找到找到至少一条长为k公共边,使得最长链的长度max length-k<=t
设length>t的边的个数为number
我们必须知道一条边是否曾被number个链同时经过,唯一的方法好像就是差分了,check函数可以写成O(n + m)的,总复杂度O((n + m)log n),60分
100分
二分答案的做法放到树上呢
考虑线性数据上二分的完整做法
预处理每一条链的length,二分答案,放到check函数里搞
没问题
LCA求出每条链的length,还是二分,check函数换成树上差分
最后发现正解只要一句话:
求链长+二分
存图
存树
struct edge{
int v,nxt,w;
}e[maxx<<1],q[maxx<<1];
inline void add_(int u,int v,int w){
e[++js].v = v;
e[js].w = w;
e[js].nxt = head[u];
head[u] = js;
}
存每一条路径(方便树上差分)
struct length{
int len,lca,u,v;//储存每一条路径的长度,lca,起点和终点
}len[maxx];
inline void addque(int u,int v){//对所求路径建图
q[++js].v = v;
q[js].nxt = headt[u];
headt[u] = js;
}
并查集
inline int find(int x){
if(f[x]==x) return x;
else
return f[x] = find(f[x]);
}
tarjan求每条链的长度,lca,以及最长链的len
void tarjan(int u,int pre){//pre前驱,防止走到自己
for (int i = head[u];i;i = e[i].nxt){
int v = e[i].v;
if(v == pre)//如果下一个点是自己的前驱就跳过
continue;
dis[v] = dis[u] + e[i].w;//存下每个点到原点的距离
tarjan(v,u);
a[v] = e[i].w;//连到v这个点的上一条边的权值;
int f1 = find(v);
int f2 = find(u);
if(f1!=f2)
f[f1] = find(f2);//存公共最先
vis[v] = 1;
}
for (int i = headt[u];i;i = q[i].nxt){
if(vis[q[i].v]){
int p = (i + 1)>>1;
len[p].lca = find(q[i].v);//塔尖求lca
len[p].len = dis[u]+dis[q[i].v]-2*dis[len[p].lca];//求链的长度(两点到原点距离-两点lca的dis*2)
maxlen = max(maxlen,len[p].len);//存下最长链,二分答案的时候用
}
}
树上差分
inline bool check(int x){
memset(s,0,sizeof(s));
num = ret = 0;//ret代表多条路径重复部分最长的边
for(int i = 1; i <= m; i++)
if(len[i].len>x){//树上差分
s[len[i].u]++;
s[len[i].v]++;
s[len[i].lca]-= 2;
num++;//记录len>x的链的个数
}
dfs(1,0);
if(maxlen-ret>x)
return 0;
return 1;
}
void dfs(int u,int pre){
for(int i = head[u];i;i = e[i].nxt){
int v = e[i].v;
if(v == pre)
continue;
dfs(v,u);
s[u]+=s[v];
}
if(s[u]==num&&a[u]>ret)
ret = a[u];
}
node
/*
work by:Ariel
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxx = 3e5 + 10;
struct edge{
int v,nxt,w;
}e[maxx<<1],q[maxx<<1];
struct length{
int len,lca,u,v;//储存每一条路径的长度,lca,起点和终点
}len[maxx];
int js,head[maxx],headt[maxx];//存图所用的变量
int dis[maxx];//记录路径
int f[maxx];//并查集
int a[maxx];//这个点前一条边的权值
int vis[maxx],maxlen;
int s[maxx];
int num,ret;
int n,m,ans;
inline void add_(int u,int v,int w){//建图
e[++js].v = v;
e[js].w = w;
e[js].nxt = head[u];
head[u] = js;
}
inline void addque(int u,int v){//对所求路径建图
q[++js].v = v;
q[js].nxt = headt[u];
headt[u] = js;
}
inline int find(int x){
if(f[x]==x) return x;
else
return f[x] = find(f[x]);
}
void tarjan(int u,int pre){//pre前驱,防止走到自己
for (int i = head[u];i;i = e[i].nxt){
int v = e[i].v;
if(v == pre)//如果下一个点是自己的前驱就跳过
continue;
dis[v] = dis[u] + e[i].w;//存下每个点到原点的距离
tarjan(v,u);
a[v] = e[i].w;//连到v这个点的上一条边的权值;
int f1 = find(v);
int f2 = find(u);
if(f1!=f2)
f[f1] = find(f2);//存公共最先
vis[v] = 1;
}
for (int i = headt[u];i;i = q[i].nxt){
if(vis[q[i].v]){
int p = (i + 1)>>1;
len[p].lca = find(q[i].v);//塔尖求lca
len[p].len = dis[u]+dis[q[i].v]-2*dis[len[p].lca];//求链的长度(两点到原点距离-两点lca的dis*2)
maxlen = max(maxlen,len[p].len);//存下最长链,二分答案的时候用
}
}
}
void dfs(int u,int pre){
for(int i = head[u];i;i = e[i].nxt){
int v = e[i].v;
if(v == pre)
continue;
dfs(v,u);
s[u]+=s[v];
}
if(s[u]==num&&a[u]>ret)
ret = a[u];
}
inline bool check(int x){
memset(s,0,sizeof(s));
num = ret = 0;//ret代表多条路径重复部分最长的边
for(int i = 1; i <= m; i++)
if(len[i].len>x){//树上差分
s[len[i].u]++;
s[len[i].v]++;
s[len[i].lca]-= 2;
num++;//记录len>x的链的个数
}
dfs(1,0);
if(maxlen-ret>x)
return 0;
return 1;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i = 1;i < n; i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add_(u,v,w);
add_(v,u,w);
}
for (int i = 1; i <= n; i++)
f[i] = i;//把每一个点的父亲设为自己(并查集初始化)
js = 0;
for (int i = 1 ;i <= m; i++){
int x,y;
scanf("%d%d",&x,&y);
len[i].u = x;
len[i].v = y;
addque(x,y);
addque(y,x);
}
tarjan(1,0);
int l = 0,r = maxlen;
while(l <= r){
int mid = (l+r)>>1;//二分
if(check(mid)){
r = mid - 1;
ans = mid;
}
else l = mid + 1;
}
printf("%d",ans);
return 0;
}