快速幂
计算a^b O(logb)
先求x=a^(b/2) ,再求a^b=x*x;
luoguP1226快速幂+取余
long long qpow(long long a,long long b,long long p)
{
long long s=1;
while(b>0)
{
if(b%2) s=s*a%p;
a=a*a%p;
b/=2;
}
return s;
}
逆元
3/7=3*1/7 所以1/7就是7的乘法逆元
mod意义下不能做除法,所以用乘法来代替,
3/7(mod 11)=3*8(mod 11)
1/7*7=1,7*8mod11=1;
P3811 乘法逆元,线性递推
费马小求逆元
(给定p)若p为质,且p不是a的约数,
根据费马小:a^(p-1)=1(mod p),所以a的逆元x=a^(p-2)
欧拉定理求逆元
若a,p互质,根据欧拉:aΦ(p)=1(mod p),所以a的逆元是aΦ(p)-1
Φ(p)是?: 对于整数p,Φ(p)表示小于等于p的与p互质的数的个数
GCD
更相减损术:gcd(a,b)=gcd(a-b,b);
辗转相除法,相当于优化过的更相减损术;
辗转相除
gcd(x,y)=gcd(x%y,y), O(log),why?:x%y<=x/2;
当y<=x/2时,x%y<y<=x/2;
当x/2<y<x时,x%y=x-y<x-x/2=x/2;
最小公倍数
lcm(a,b)=a*b/gcd(a,b);
扩展GCD
利用gcd思想可以求一组不定方程的解,给定a,b,求ax+by=gcd(a,b)的解;

其中符号a/b为下取整;
通过上面的方法只能求出无数个解其中的一个,
通解为: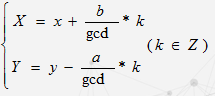
无解的情况???
ax+by=c,这个方程什么时候时无解?
c不是gcd(a,b)的倍数时;
推广到一般
以上知道如何求ax+by=gcd(a,b)后,那么如何求ax+by=c(保证有解)呢?
我们令k=c/gcd,那就相当于求k(ax+by)=gcd(a,b)*k,
那么就求出ax+by=gcd(a,b)的解,再将解*k即可;
同余
什么是同余?a≡b(mod m) → a mod m=b mod m???
不对,上面的式子没有考虑负数的情况;
正确的解释为:a≡b(mod m) → (a-b) mod m=0;
EG:
求关于x的同余方程ax≡1(mod b)的最小正整数解,2<=a,b<=2*10^9;
将原式转化为exgcd形式,相当于求ax-by=1;
若a,b不互质肯定无解,用exgcd求出一组解,再求最小正整数解,
只是某一组解就能求最小?
根据x加上b/gcd(a,b),同时y减去a/gcd(a,b)后,仍满足ax+by=c
/*
ax≡1( mod b)等价于ax+by=1。
那么题目就转化成求这个表达式x的最小值。
可以把1看成gcd(a,b),于是就变成求解exgcd了。
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
int a,b,x,y;
int exgcd(int a,int &x,int b,int &y)
{
if(b==0)
{
x=1;
y=0;
return a;
}
int s=exgcd(b,x,a%b,y);
int k=x;
x=y;
y=k-a/b*y;
return s;
}
int main()
{
scanf("%d%d",&a,&b);
exgcd(a,x,b,y);
printf("%d",(x+b)%b);
return 0;
}
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,num,x;
int pri[10000002];
bool b[10000002];
bool judge(int n)
{
for(int i=2;i<=n;++i)
{
if(!b[i]) pri[++num]=i;
for(int j=1;j<=num;++j)
{
if(i*pri[j]>n) break;
b[i*pri[j]]=1;
if(i%pri[j]==0) break;
//这句话保证了每个数只会被筛O(1)次,只会被自己最小的质因子筛掉
}
}
}
int main()
{
scanf("%d%d",&n,&m);
b[1]=1;
judge(n);
while(m--)
{
scanf("%d",&x);
if(b[x]) printf("No
");
else printf("Yes
");
}
return 0;
}
这个题,这份代码一定要注意的是bool b数组0和1对应的到底是还是不是质数!
欧拉函数

公式?
线性筛法求欧拉函数
for(int i=2;i<=n;++i)
{
if(!b[i])
{
pri[++num]=i;
olar[i]=i-1;
}
for(int j=1;j<=num;++j)
{
if(i*pri[j]>n) break;
b[i*pri[j]]=1;
if(i*pri[j]!=0)
olar[i*pri[j]]=olar[i]*(pri[j]-1);
if(i%pri[j]==0)
{
olar[i*pri[j]]=olar[i]*pri[j];
break;
}
}
}
//相当于线性筛素数的时候顺道求出欧拉函数
非常有必要解释一下pri和olar这两个数组的意义,:
pri记录1~n中所有的素数,也就是说,pri[i]表示的是第i个质数是多少,;
olar当然就是欧拉函数了,olar[i]表示的是1~i中质数的个数,;
EG:
给出一个数n,求比n小且与n互质的数的和,n<=10^7;
答案就是n*olar[n]/2,互质的数是一对的,
gcd(a,n)=gcd(n-a,n)=1;
组合数

有序:n=3有6(n!)种排列,
无序:n!种算作一种,那么就有(n!-1)种都是重复的;
※放挡板问题;(不能解决0)
※0的话就先都+1,最后再-1;
先要知道杨辉三角:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
杨辉三角的性质:
第n行的元素个数有n个;
第n行的所有元素之和为2*(n-1)?;
第n行第m个数的值为C(n-1, m-1),其中C为组合数;
(a+b)n展开后的各项系数等于第n+1行的值;
第n行第m个数的奇偶判断,及C(n-1,m-1)的奇偶判断:
(m-1)&(n-1)==(m-1)? 奇:偶;
(证明见http://www.cnblogs.com/Muia/p/5746491.html)
杨辉三角的应用:
最好的应用之一就是减少求组合数的复杂度:
将杨辉三角的值打印出来后,只需要查表即可得到正确结果,
这个对于求排列组合数非常有用;
另外一种Lucas定理
#%……¥%……&¥#@¥%
(常与数位DP结合,)
求组合数的另一种方法
给定o<=n<=m<=10^5,1<p<10^9;
q组数据,计算C(m,n)mod p;
※预处理出阶乘,和阶乘的逆元,直接计算???;O(m+n+q);
一些组合数有用的公式

要特别知道的是5和4;
容斥原理
eg:一道小学奥数,


答案为:4+17+18+15-6-6-5+2=39
容斥原理图:


斐波那契数列
f(0)=1,f(1)=1;
f(n)=f(n-1)+f(n-2),n>=2
卡特兰数
C(1)=1;
C(n+1)=C(1)C(n)+C(2)C(n-1)+...+C(n)C(1)
Eg:
n个数要进栈然后出栈,问出栈顺序有多少种?
设f(n)为n个数的答案,枚举最后一个出栈的为k,那么
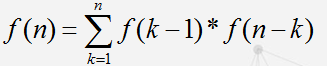
P1044 卡特兰数,栈(两种操作)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
int main()
{
int n;
long long int f[100000];
cin>>n;
f[0]=f[1]=1;
for(int i=2;i<=n;i++)
f[i]=f[i-1]*(4*i-2)/(i+1);
cout<<f[n];
}
Eg:
给定n个节点,求能生成多少个不同形状的二叉树?
设f(n)为n个数的答案,枚举左子树大小为k

卡特兰数通项公式
C(n+1)=C(2n,n)-C(2n,n-1)
折线法
例题%……&&*@¥¥%……
走方格,不能穿过对角线#%……&##@%
错排
一个有n个元素的序列,若这n个元素都不在自己原来的位置上,那么这样的排列就被称为错排;
i个元素的错排方案数为D(i);
推导公式
D(n)=(n-1)[D(n-1)+D(n-2)]
D(1)=0,D(2)=1;
推导方法:
第一步将n放到位置k,k<n,有n-1种放法;
第二步若将k放到位置n,那么就有D(n-2)种放法,否则就有D(n-1)种放法;
Eg:
有n本书,n个位置,每一本书放一个位置;求恰好有m本书放对位置的方案数;
答案为:C(n,m)*D(n-m);
高斯消元
最大用途:解多元一次方程组;


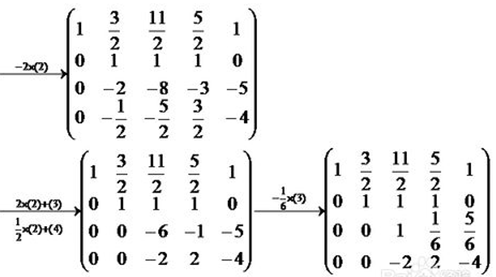
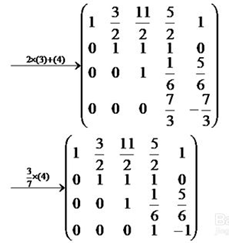
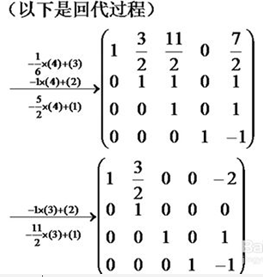

抑或高斯消元
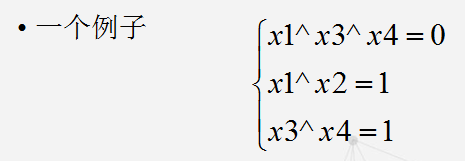
相当于把原来方程组中的+和-换成^操作;
概率与期望
定义?
举一个简单的例子:你有0.8的概率拿50分,0.2的概率拿100分,你的期望得分便为0.8*50+0.2*100=60分
0.8,0.2就是概率,60就是期望;
贝叶斯公式
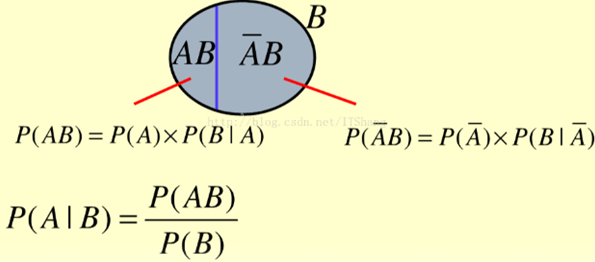
两个独立(没有关系的)事件的概率可相加;
E(A+B)=E(A)+E(B);
P(B|A):表示在A一定发生的情况下,B发生的概率;
①:如果AB独立,P(B|A)=P(B);
②:P(B|A)*P(A)=P(AB)(贝叶斯)
P(AB):若两个独立,P(AB)=P(A)*P(B);
Eg:

这个题目比较简单,我们只需要想:已经拿走一个白球,还剩9个,那么再拿到一个红球,概率就为3/9=1/3
但是这只是比较简单的问题,而对于较复杂的问题来说,还是要依靠贝叶斯公式,
此题方法为:A表示第一次拿到白球,B表示第二次拿到红球,
P(A)=1/10 P(AB)=1/30 P(B|A)=P(AB)/P(A)=1/3
DP类型的期望题
一般有两种设法
f(i)表示i到终点的期望,然后按照i递减来推。
f(i)表示起点到i的期望,然后按照i递增来推。
一般前者用得较多
例如我要从0号点到n号点,一次可以走一步或者两步,问到达终点的期望;
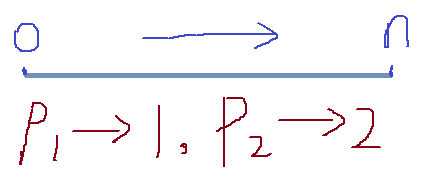
初始化f(n)=0,
f(i)=p1*(f(i+1)+1)+p2*(f(i+2)+1);
矩阵乘法
一个n行m列的矩阵A*一个m行p列的矩阵B=一个n行p列的矩阵C;
A*B A第一行*B第一列
公式:
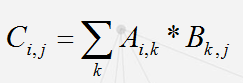
时间复杂度O(nmp),
性质:一般不满足交换律,满足结合律;A*B*C=A*(B*C)
那么结合律有什么好处呢?答曰:相同的东西合到一起用快速幂;
比如:求A*B*A*B*A*B ,就可以计算(A*B)*(A*B)*(A*B)
Eg:
求斐波那契第n项mod p,n<=10^15
我们把它看做一个1*2的矩阵,也就是:

求得?也就是矩阵B为

所以啊,

也就是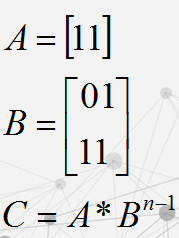
矩阵C的左上角就是答案,
矩阵乘法的功能之一:优化DP;
Eg:
现在要向前走n个单位的距离,每一步的步长为[1,k]个单位,问走完n个单位可以有多少种不同的方法;
n<=10^15,k<=7;
和上面类似,如果k=4,那么f[n]=f[n-1]+f[n-2]+f[n-3]+f[n-4]
转移矩阵就为:
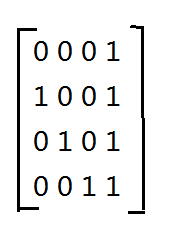
k=3时,
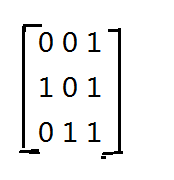
Eg※:
给你三个N*N的矩阵A B C,问A*B在mod p意义下是否等于C;n<=1000
直接判断的话是1000^3,过不了,我们尝试构造几个1*n的随机矩阵D,
判断D*A*B是否等于D*C,每次判断的时间复杂度为O(n^2);
矩阵D是为了减少复杂度的,可以降到O(n^2),间接判断A*B是否=C