简述
什么是树状数组呢,顾名思义就是树一样的数组,本质就是用数组模拟树形结构。
树状数组有什么用呢,树状数组可以实现单点更新,单点查询,区间查询和区间更新,维护的东西和线段树可以类比的,就是满足区间加法性质的属性,例如最值,和,gcd等。
树状数组可以干的东西线段树也能干,但线段树干的东西树状数组不一定能干。树状数组的复杂度和线段树同级,但常数更低且代码量更为简答,所以我们能用树状数组就用树状数组,这样就不容易TLE了hhh。
lowbit操作
首先我们来了解一个操作,lowbit(x),这个操作取出x二进制最低位的1,例:lowbit(10100)=100
代码实现为x&(-x)。
ll lowbit(ll x){ return x&(-x); }
为什么是x&(-x)呢?我们知道对一个数取负就是对这个数取反加一。我们设原数的二进制为xxx1000...,该数取反为yyy0111...,令其加一,我们可以发现,取反加一后的数只有一位是1,且该位置就是原数最低位的1,所以我们令x&(-x)就可以得到x的lowbit了。
树的样子
对于一般的二叉树,形状是这样的
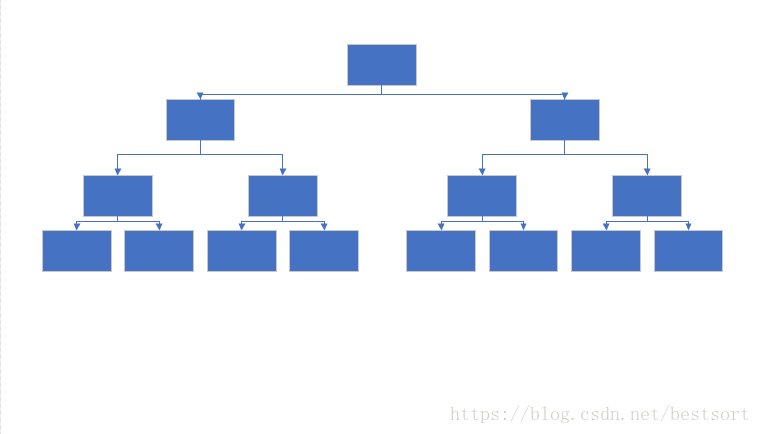
此时我们令其偏一下身子,使其右倾变为这样
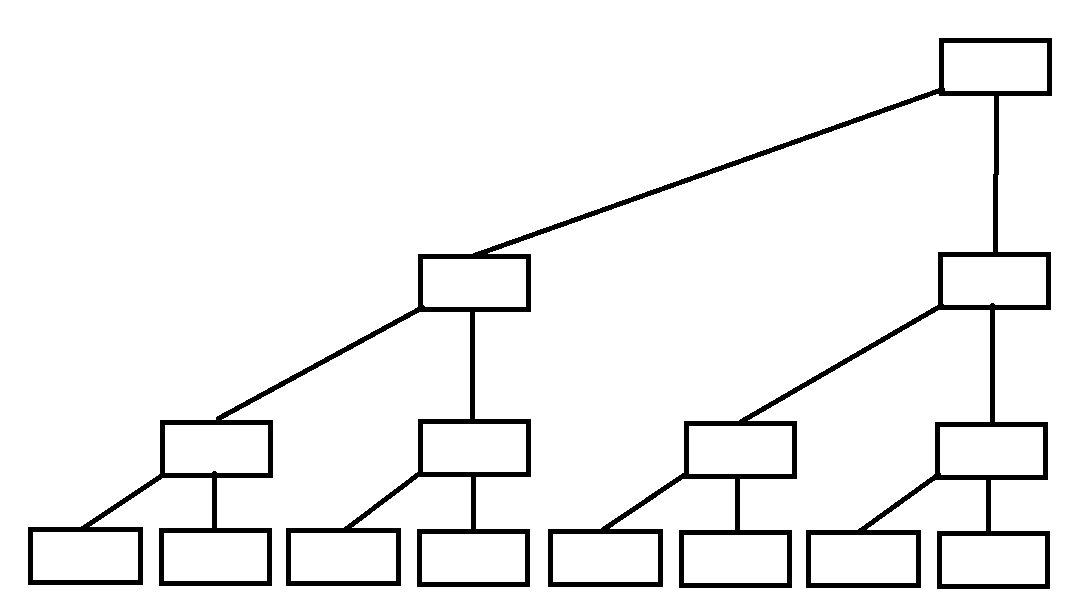
如果每个节点都存东西,那就不叫树状数组叫线段树了,那他们有什么不同呢?我们来看下图:

底下的代表我们输入的a数组,上面的代表我们的树状数组c数组。从空间上来说,树状数组只需要存二叉树的根和左子树就行,因为右子树可以由根减左子树获得,则有:
•C[1] = A[1];
•C[2] = A[1] + A[2];
•C[3] = A[3];
•C[4] = A[1] + A[2] + A[3] + A[4];
•C[5] = A[5];
•C[6] = A[5] + A[6];
•C[7] = A[7];
•C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
可以发现,这颗树是有规律的,我们可以发现,C[i]存了从i开始往前数共lowbit(i)个位置的和。
单点更新
例如我们需要令a[1]+=k,则需要维护c1,c2,c4,c8这些包含a1的节点,我们可以发现这些需要维护的节点是层次关系:c1<c2<c4<c8,也就是说我们只要更新本节点以及本节点的所有父亲就可以实现更新操作,而本结点兄弟维护的叶子数和本节点维护的相同,还记得之前我们观察的规律C[i]存了从i开始往前数共lowbit(i)个位置的和吗,我们只需要加上lowbit(本节点的下标),即可得到本节点的父亲,一直递归到根,就完成了更新。
void update(int x,int val,int n){ //x位置的值加上val,n为总叶子个数 for(int i=x;i<=n;i+=lowbit(i)){ c[i]+=val; } }
区间查询
例如我们需要查询区间3到5的和,其值等于a3+a4+a5,如果我们得到前缀和sum[i],其值就等于sum[5]-sum[2],而树状数组恰恰就是利用了前缀和求出区间和。
例如我们要求sum(7),那么sum(7)=c[7]+c[6]+c[4],我们可以很容易看出,6是由7-lowbit(7)得到的,4是由6-lowbit(6)得到的,而4减它的lowbit就等于0了。我们可以知道,sum(i)可由每个c位置的贡献求出,每个位置为上个位置减lowbit。为什么可以这样呢,我们来看i=2的幂时,这时c[i]就完全包含1到i这i个元素,无需做任何处理,当i不是2的幂时,需要一个一个处理,直到i消掉低位的1变为2的幂,例如i=7的时候,一开始lowbit(7)=1,也就是说c[7]只维护了一个节点那就是a[7],令其减loewbit,得i=6,此时c6维护了a5和a6两个节点,减去lowbit得i=4,包含1到i所有节点,故加上贡献后结束。
所以下一个有贡献的位置是当前位减lowbit(当前)。
ll sum(int x){ ll ans=0; for(int i=x;i>=1;i-=lowbit(i)){ ans+=c[i]; } return ans; }
模板

#include<iostream> using namespace std; const int maxn=1e5+5; typedef long long ll; ll lowbit(ll x){ return x&(-x); } void update(int x,int val,int n){ for(int i=x;i<=n;i+=lowbit(i)){ c[i]+=val; } } ll sum(int x){ ll ans=0; for(int i=x;i>=1;i-=lowbit(i)){ ans+=c[i]; } return ans; } int main() { return 0; }
