K均值聚类和代码实现

　　K均值聚类是一种无监督学习聚类算法。

介绍

　　对于$n$个$m$维特征的样本，K均值聚类是求解最优化问题：

$displaystyle C^*= ext{arg}minlimits_{C}sumlimits_{l = 1}^Ksumlimits_{C(i)=l}||x_i-overline{x}_l||^2$

　　其中$C$表示某个样本的划分，$C(i)=l$表示$x_i$被划分到$第l$类。所以上式表示最小化所有类别内样本到其对应的类别样本均值的距离之和。最优化这个问题是NP难问题，所以现实采用类似贪心的迭代算法来逼近最优解（不一定最优）。具体流程如下（每个样本只能属于一个类别）：

　　0、初始化$K$个类的均值为随机$m$维向量。

　　1、将每个样本划分到与之距离最小的类别均值对应的类别中。

　　2、根据划分进的样本，每个类别重新计算类别均值，并记录。

　　3、比较连续两次的类别均值，如果差别小于一定阈值就结束，否则回到1。

　　通过计算可以知道时间复杂度是$O(mnk)$。

代码实现

Numpy手动实现

　　首先使用由正态分布生成的两簇点集来实验，每个簇各200个点。可能由于这两个点集比较靠近，所以分类完全错误，如图：

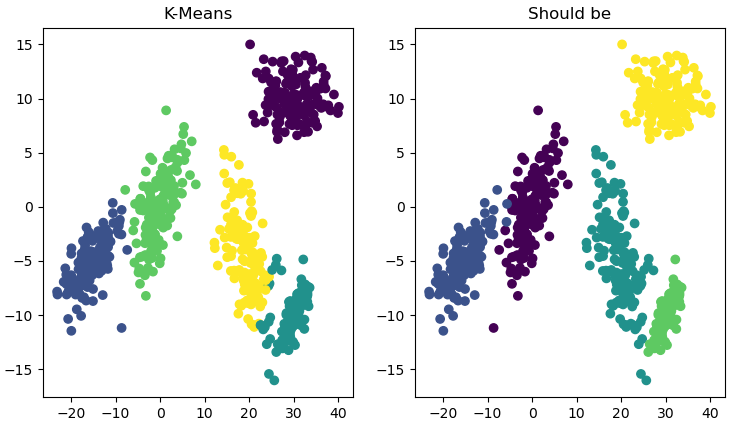
 　　重新生成5簇正态分布点集，这次每个集合之间相对较远，除了少数没有正确聚类外（两类交汇处），表现不错：

 　　代码如下：

#%%获取数据
import matplotlib.pyplot as plt
import numpy as np 
import xlrd 

table = xlrd.open_workbook('test.xlsx').sheets()[0]#读取Excel数据
data = []
for i in range(0,table.nrows):#假设第一行是表头不读入
    data.append(table.row_values(i))   
data = np.array(data)  
#%%聚类
def distance(a,b):
    d = a-b
    return np.dot(d,d) 
def clusterize(data,class_m):#关于类均值对样本分类
    for i in data:
        min_dis = np.inf
        for j in range(len(class_m)):
            t = distance(i[:-1],class_m[j])
            if t<min_dis:
                min_dis=t
                i[-1]=j
                
def calc_mean(data,class_m):#以类中样本计算均值
    class_m -= class_m
    num = np.zeros([len(class_m)])
    for i in data:
        num[int(i[-1])]+=1
        class_m[int(i[-1])]+=i[:-1]
    for i in range(len(class_m)):
        class_m[i]/=num[i]
def updated_mean(dif):#计算前后两次更新的均值距离，传入前后差值
    sum_ = 0
    for i in dif:
        sum_ += np.dot(i,i)
    return sum_ 
def k_means_cluster(data,K):
    class_mean = data[0:K,:-1]
    class_mean_old = -class_mean
    t = updated_mean(class_mean-class_mean_old) 
    ii = 0
    while t>0.0001:
        class_mean_old = class_mean.copy()
        clusterize(data,class_mean) 
        print(class_mean)
        print(class_mean_old)
        calc_mean(data,class_mean)
        print(class_mean)
        print(class_mean_old)
        t = updated_mean(class_mean-class_mean_old)
        print(t)
        ii+=1
        print(ii)
data1 = data.copy()
np.random.shuffle(data1)
k_means_cluster(data1,5) #要分几类直接这里设置##################################

#%%绘制结果
import matplotlib.pyplot as plt

fig = plt.figure()
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.scatter(data1[:,0],data1[:,1],c = data1[:,-1])
ax1.set_title("K-Means")
ax2.scatter(data[:,0],data[:,1],c = data[:,-1])
ax2.set_title("Should be")
plt.show() 

Sklearn

　　使用封装好的Sklearn，代码如下：

#%%获取数据
import matplotlib.pyplot as plt
import numpy as np 
import xlrd 

table = xlrd.open_workbook('test.xlsx').sheets()[0]#读取Excel数据
data = []
for i in range(0,table.nrows):#假设第一行是表头不读入
    data.append(table.row_values(i))   
data = np.array(data)   
#%%聚类
from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=5)
kmeans.fit(data[:,:-1])
y = kmeans.predict(data[:,:-1])  
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.scatter(data[:,0],data[:,1],c = y)
ax1.set_title("K-Means")
ax2 = fig.add_subplot(122)
ax2.scatter(data[:,0],data[:,1],c=data[:,-1])
ax2.set_title("Should be")
plt.show()

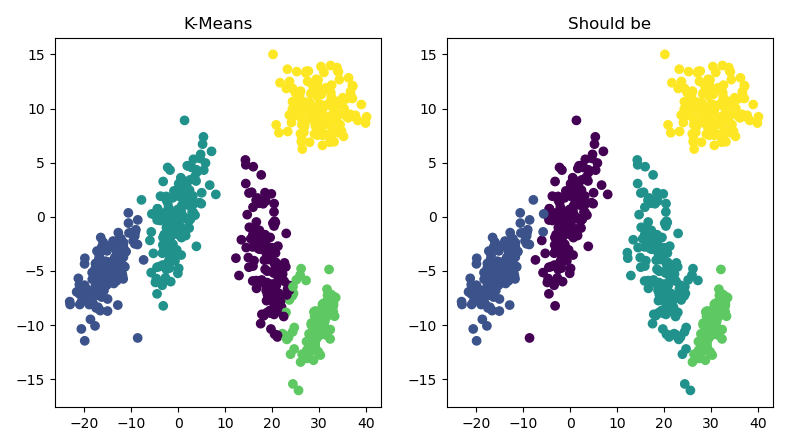
　　结果图：