一:树的基础
树由节点和边构成,两个节点之间有且仅有一条边连接。故此,一棵树是N个节点和N-1条边的集合。如图:
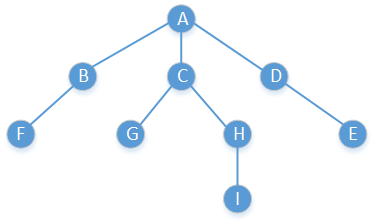
若树非空,则树由根节点A,及0个或多个非空子树构成;每颗子树的根都是根A的儿子child,而A是每颗子树的根的父亲,除根节点A以外,每一个节点都有一个父亲。每个节点都可以有任意多个儿子,我们将没有儿子的节点称为“树叶”,具有同一个父亲的节点称为“兄弟”,类似的有“祖父”、“孙子”,如下图:

深度:某一节点n,n到根节点A的路径长度即为深度。A深度为0
高度:某一节点n,n到某一树叶节点的最长路径即为高度。所有树叶高度为0.(说某一节点的高度,可以把该节点看成是“地面”,地面到根的长度即为“深度”,到树叶的最长路径为“高度”)
二:树的遍历
目录结构是典型的树的应用,
先序遍历(目录)、后序遍历(磁盘大小)、中序遍历(表达式树)
三、二叉树
二叉树是树在执行‘二胎政策’后的产物,即儿子个数不得大于2。在相同节点个数N的情况下,这个政策有效控制了树的深度,即二叉树的深度比节点个数N小得多。但是在最坏情形下,深度可以达到N-1;
3.1:二叉查找树ADT:对于树中的每个节点N,N的左子树中所有项小于N中的项,而N的右子树种的所有项都大于N中的项。平均深度O(logN)
ADT在不断进行交叉删除、插入后,会变得不平衡,从而深度得不到控制。故而加入一种平衡策略:任何节点深度不得过深。--》AVL树:加入平衡条件之后的二叉查找树。
平衡条件:每个节点的左右子树高度差不得大于1.(空树高度定为-1)
加入不同的平衡方案,构成不同的平衡树,例如B树、红黑树、赋权平衡树等。
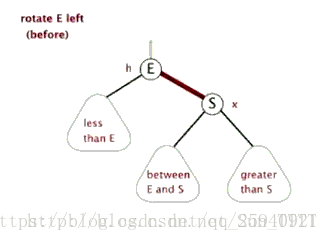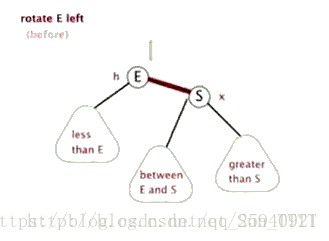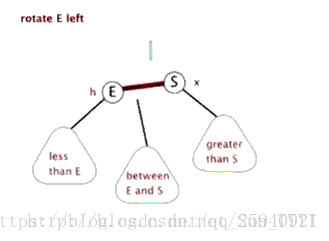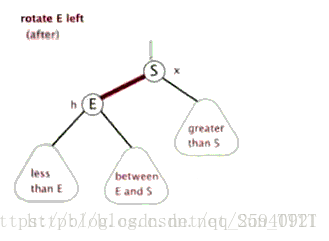
为了保证平衡条件:引入操作:单旋转、双旋转
左旋:
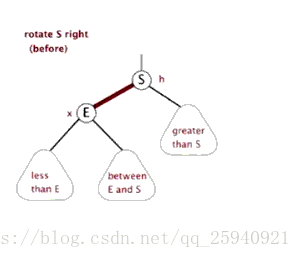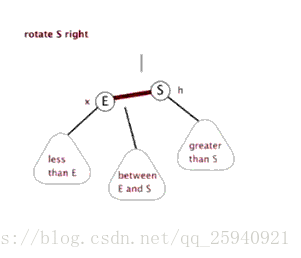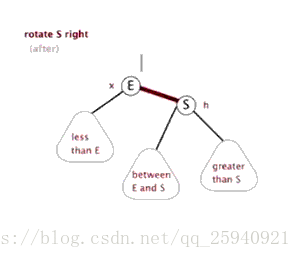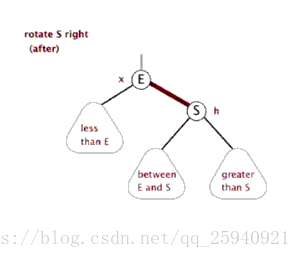
右旋:
双旋:先左后右、先右后左。