如果某一幅图像的直方图覆盖了灰度级很宽的范围,分布均匀,则该图像具有高对比度、多变的灰度色调且动态范围大,如下图所示[1]。

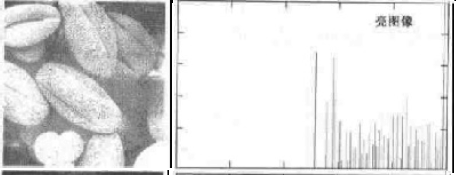
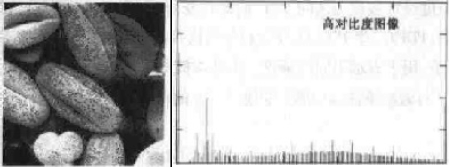
直方图均衡可以使得图像的直方图分布均匀化,拉大灰度间隔,有利于图像的分析和识别。为说明直方图均衡原理,我们假设某一图像有8个灰度级,其原始直方图如下:
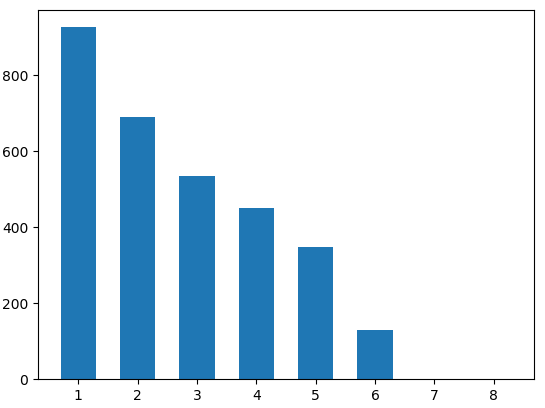
我们通过如下的表格来说明直方图均衡原理课,表格中ni表示图像中出现在该灰度级的次数,n表示图像中像素总数目。
| 灰度级 | 原始直方图ni | 原始直方图概率p=ni/n | 累积概率H |
新灰度级=H*8(四舍五入取整) |
新直方图 |
| 1 | 927 | 0.301 | 0.301 | 2 | 0 |
| 2 | 690 | 0.224 | 0.525 | 4 | 927 |
| 3 | 535 | 0.174 | 0.699 | 6 | 0 |
| 4 | 450 | 0.146 | 0.845 | 7 | 690 |
| 5 | 348 | 0.113 | 0.958 | 8 | 0 |
| 6 | 129 | 0.042 | 1.0 | 8 | 535 |
| 7 | 0 | 0 | 1.0 | 8 | 450 |
| 8 | 0 | 0 | 1.0 | 8 | 477 |
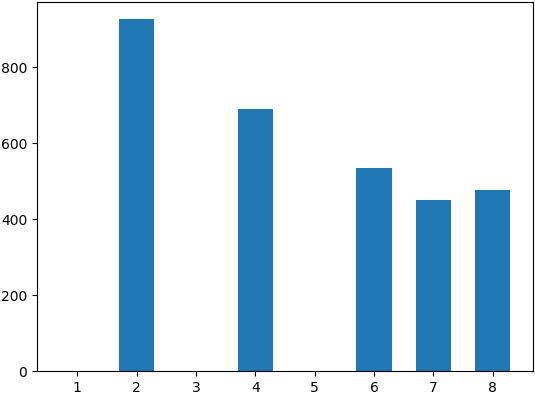
直方图均衡化之后,图像的直方图如下图所示:
【参考文献】
[1] 《数字图像处理》冈萨雷斯