本人没有打这场 CF,但是场外看到这套题觉得很多题都很有趣,于是写个题解分享一下。
本场比赛链接:https://codeforces.com/contest/1395 。
A - Boboniu Likes to Color Balls
这些字符可以构成回文串当且仅当至少三种字符的个数要是偶数。
然后我们又发现一次操作相当于奇偶互换,但是又没有这么简单,要特判 \(r,g,b=0\) 的情况。记当前个数是偶数的字符种数为 \(x\),分两类情况讨论:
- \(x>2\),则肯定可以满足。
- \(x<3\),这时再分成三类讨论:
1、\(r=0\) 或 \(g=0\) 或 \(b=0\),则没有办法执行操作,永远无法满足回文的条件。
2、\(r,g,b\ne 0,x=2\),则不论这么操作都是两奇两偶,无法满足回文的条件。
3、\(r,g,b\ne 0,x=1\),则只需要进行一次操作,就可以满足回文的条件。
Code
#include <stdio.h>
using namespace std;
int tt,r,g,b,w;
int main()
{
scanf("%d",&tt); int o;
while (tt--)
{
scanf("%d%d%d%d",&r,&g,&b,&w);
o=(r%2==0)+(g%2==0)+(b%2==0)+(w%2==0);
if (o>2) puts("Yes");
else if (!r||!g||!b) puts("No");
else
{
if (o==2) puts("No");
else puts("Yes");
}
}
return 0;
}
B - Boboniu Plays Chess
这道题我们需要先把当前所在行的所有格子全都走一遍,然后从第一行开始,按顺序走完所有未走过的行,但是每走完一行,接下来走的方向需倒过来(比如你某一行是从左往右的方向走的,那么你下一未走过的行就要从右往左方向走)就可以了。(简单来说就是 S 形走位就可以了)
但是还有更简单的做法,注意到 \(n,m\le 100\),所以直接 dfs 即可。
Code
#include <stdio.h>
#include <math.h>
#include <cstdlib>
#define il inline
using namespace std;
const int N=205;
int n,m,sx,sy;
int ok[N][N],p[N*N],q[N*N];
il void dfs(int x,int y,int c)
{
int i;
if (c>n*m){for (i=1; i<=n*m; i++) printf("%d %d\n",p[i],q[i]);exit(0);}
for (i=1; i<=n; i++) if (!ok[i][y])
ok[i][y]=1,p[c]=i,q[c]=y,dfs(i,y,c+1),ok[i][y]=0;
for (i=1; i<=m; i++) if (!ok[x][i])
ok[x][i]=1,p[c]=x,q[c]=i,dfs(x,i,c+1),ok[x][i]=0;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&sx,&sy);
ok[p[1]=sx][q[1]=sy]=1,dfs(sx,sy,2);
return 0;
}
C - Boboniu and Bit Operations
首先,我们求出每个 \(c_{i,j}=a_i\& b_j\)。
然后我们从高位到低位贪心,根据或运算的特点,只有全部是 \(0\) 才是 \(0\),设当前位为 \(k\)。
那么如果不存在 \(i,j\),使得 \(c_{i,j} >> k \& 1=0\),那么只能是 \(1\),这时候计算贡献;如果存在 \(i,j\),使得 \(c_{i,j}>>k\& 1=0\),那么这时候不需要计算贡献,而是把满足 \(c_{i,j}=1\) 的 \((i,j)\) 删掉即可。
时间复杂度为 \(O(nm\log)\),空间复杂度为 \(O(nm)\)。
Code
#include <stdio.h>
#include <algorithm>
using namespace std;
const int N=205;
int n,m,ans,t,a[N],b[N][N];
int main()
{
scanf("%d%d",&n,&m); int i,j,k,o1,o2;
for (i=1; i<=n; i++) scanf("%d",a+i),t=max(t,a[i]);
for (j=1; j<=m; j++)
{
scanf("%d",&k),t=max(t,k);
for (i=1; i<=n; i++) b[i][j]=a[i]&k;
}
for (k=9; ~k; k--) if ((1<<k)<=t)
{
for (i=o1=1; i<=n; i++)
{
for (j=o2=1; j<=m; j++) if (b[i][j]>=0&&!(b[i][j]>>k&1)){o2--;break;}
if (o2){o1--;break;}
}
if (!o1) ans+=1<<k;
else{for (i=1; i<=n; i++) for (j=1; j<=m; j++) if (b[i][j]>>k&1) b[i][j]=-1;}
}
printf("%d",ans);
return 0;
}
D - Boboniu Chats with Du
我们按照与 \(m\) 的大小关系分作两类,如果我们选了不超过 \(m\) 中的 \(s\) 个,那么我们就可以选超过 \(m\) 中的 \(\lceil \frac{n-s}{d+1} \rceil\) 个。
那么我们排个序,分别求出 \(p_i,q_i\),表示不超过/超过 \(m\) 中选 \(i\) 的最大价值,则答案就是 \(\max\limits_{0\le i\le P}\{p_i+q_{\lceil\frac{n-i}{d+1}\ \rceil}\}\),其中 \(P\) 是不超过 \(m\) 的个数。
时间复杂度为 \(O(n\log{n})\),瓶颈在排序上,空间复杂度为 \(O(n)\)。
Code
#include <stdio.h>
#include <algorithm>
#define int long long
using namespace std;
const int N=1e5+5;
int n,d,m,ans,a[N];
int b[N],s1,c[N],s2;
signed main()
{
scanf("%lld%lld%lld",&n,&d,&m),d++; int i;
for (i=1; i<=n; i++) scanf("%lld",a+i);
sort(a+1,a+n+1);
for (i=n; i; i--)
if (a[i]>m) s2++,c[s2]=c[s2-1]+a[i];
else s1++,b[s1]=b[s1-1]+a[i];
for (i=0; i<=s1; i++) ans=max(ans,b[i]+c[(n-i+d-1)/d]);
printf("%lld",ans);
return 0;
}
E - Boboniu Walks on Graph
这道题我觉得蛮有意思的。
首先肯定要将每条边的出边按照边权排序,这里的时间复杂度为 \(O(n\log{n})\)。
然后 dfs 的时间复杂度为 \(O(k!)\)。
我们还发现,\((c_1,c_2,\cdots,c_k)\) 合法等价于按照这个 \(k\) 元组连完边后,每个点有且只有一条出边。
朴素判断是 \(O(n)\) 的,如果这样复杂度将无法接受,考虑怎么优化这个判断过程。
最直接的想法就是 bitset,时间复杂度为 \(O(\frac{nk!}{\omega})\),空间复杂度为 \(O(\frac{n^2}{\omega})\),大力卡常是可以过的,但是这里不讲这个做法。
我们考虑预处理出 \(S_{i,j}\),表示 \(c_i=j\) 时会被占用的点的集合。那么我们 dfs 的时候只需要判断当前的集合与 \(S_{i,j}\) 的交集是否为空,最后所有的集合并完后是不是 \({1,2,\cdots,n}\)。
我们将集合哈希一下,转化为哈希值,这样就可以做到 \(O(1)\) 判断。
本人采用双哈希,防止被叉,时间复杂度为 \(O(n\log{n}+k!)\),空间复杂度为 \(O(n^2+m)\)。
Code
#include <stdio.h>
#include <algorithm>
#include <vector>
#define il inline
#define ll long long
using namespace std;
const int N=2e5+5; const ll P1=998244353,P2=1e9+7;
int n,m,k; vector<pair<int,int> > e[N]; vector<int> v[10];
ll ans,s1,s2,t1[N],t2[N],p1[10][10],p2[10][10];
il void dfs(int c,ll p,ll q)
{
if (c>k){ans+=(p==s1&&q==s2);return;} int i;
for (i=0; i<c; i++) dfs(c+1,(p+p1[c][i])%P1,(q+p2[c][i])%P2);
}
int main()
{
scanf("%d%d%d",&n,&m,&k); int i,j,w;t1[0]=t2[0]=1;
for (i=1; i<=n; i++) s1=(s1+(t1[i]=t1[i-1]*2347623ll%P1))%P1,s2=(s2+(t2[i]=t2[i-1]*19260817ll%P2))%P2;
while (m--) scanf("%d%d%d",&i,&j,&w),e[i].push_back(make_pair(w,j));
for (i=1; i<=n; i++) sort(e[i].begin(),e[i].end()),v[e[i].size()].push_back(i);
for (i=1; i<=k; i++) for (j=0; j<i; j++)
{
for (auto w:v[i]) p1[i][j]=(p1[i][j]+t1[e[w][j].second])%P1,p2[i][j]=(p2[i][j]+t2[e[w][j].second])%P2;
}
dfs(1,0,0),printf("%lld",ans);
return 0;
}
F - Boboniu and String
这道题我觉得也蛮有意思的。
首先显然,串 \(S\) 与 \(T\) 是相似的当且仅当两个串的字符 B 与字符 N 的个数都相同。
而操作等价于我们将串 \(S\) 的字符 B 或者 N 的数量减少或增加一,或者让字符 B 和 N 的数量同时增加或者减少一。
我们将字符 B 的数量当作横坐标,字符 N 的数量当作纵坐标,那么如果限制 \(k\) 步就要相似,则如下范围内的串都可以满足要求:
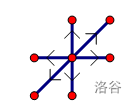
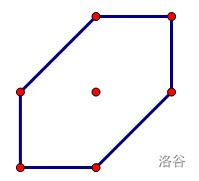
这个平面区域我们用线性规划的方法,用一个不等式组表示出来:
设第 \(i\) 个字符串的坐标为 \((x_i,y_i)\)。
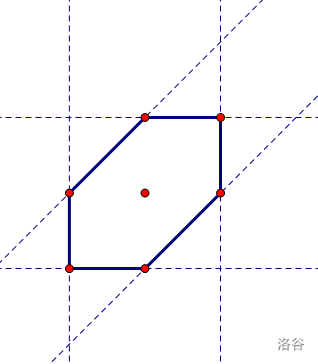
我们二分答案,建出这 \(n\) 个区域,判断这 \(n\) 个区域有没有交即可。
接下来考虑构造一个方案:
假设我们如上求出了 \(x,y,x-y\) 的范围,分别为 \(x\in [X_1,X_2],y\in [Y_1,Y_2],x-y\in [Z_1,Z_2]\)。
那么显然有 \(x \in[Y_1+Z_1,Y_2+Z_2]\),与 \([X_1,X_2]\) 取交集后求出 \(x\) 的一个值,然后便有 \(y\in[x-Z_2,x-Z_1]\),与 \([Y_1,Y_2]\) 取交集后求出 \(y\) 的一个值,即可。
时间复杂度为 \(O(n\log{n})\),空间复杂度为 \(O(n)\)。
Code
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define il inline
using namespace std;
const int N=5e5+5;
int n,ans,x[N],y[N],X1,X2,Y1,Y2,Z1,Z2; char s[N];
il void work(int l)
{
int i; X1=Y1=Z1=-1e9,X2=Y2=Z2=1e9;
for (i=1; i<=n; i++)
X1=max(X1,x[i]-l),X2=min(X2,x[i]+l),
Y1=max(Y1,y[i]-l),Y2=min(Y2,y[i]+l),
Z1=max(Z1,x[i]-y[i]-l),Z2=min(Z2,x[i]-y[i]+l);
}
il int check(int l)
{
work(l);
if (X1>X2||Y1>Y2||Z1>Z2||X1-Y2>Z2||X2-Y1<Z1) return 0;
return 1;
}
int main()
{
scanf("%d",&n); int i,j,l,r,mid;
for (i=1; i<=n; i++)
{
scanf("%s",s+1),l=strlen(s+1);
for (j=1; j<=l; j++)
if (s[j]=='B') x[i]++;
else y[i]++;
}
for (l=0,r=N+N; l<=r; )
{
mid=l+r>>1;
if (check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%d\n",ans),work(ans),X1=max(X1,0),Y1=max(Y1,0);
l=min(X2,Y2+Z2),r=min(l-Z1,Y2);
while (l--) putchar('B'); while (r--) putchar('N');
return 0;
}