(color{#0066ff}{ 题目描述 })
小强要在(N)个孤立的星球上建立起一套通信系统。这套通信系统就是连接(N)个点的一个树。 这个树的边是一条一条添加上去的。在某个时刻,一条边的负载就是它所在的当前能够 联通的树上路过它的简单路径的数量。
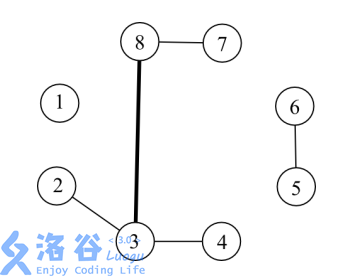
例如,在上图中,现在一共有了(5)条边。其中,((3,8))这条边的负载是(6),因 为有六条简单路径(2-3-8),(2-3-8-7),(3-8),(3-8-7),(4-3-8),(4-3-8-7)路过了((3,8))。
现在,你的任务就是随着边的添加,动态的回答小强对于某些边的负载的 询问。
(color{#0066ff}{输入格式})
第一行包含两个整数 (N, Q),表示星球的数量和操作的数量。星球从 (1) 开始编号。
接下来的 (Q) 行,每行是如下两种格式之一:
A x y表示在 (x)和 (y) 之间连一条边。保证之前 (x) 和 (y)是不联通的。Q x y表示询问 ((x,y)) 这条边上的负载。保证 (x) 和 (y) 之间有一条边。
(color{#0066ff}{输出格式})
对每个查询操作,输出被查询的边的负载。
(color{#0066ff}{输入样例})
8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8
(color{#0066ff}{输出样例})
6
(color{#0066ff}{数据范围与提示})
对于所有数据,(1≤N,Q≤10^5)
(color{#0066ff}{ 题解 })
众所周知,LCT是维护树链的强力数据结构
对于维护一个子树的信息,是不太好维护的
但是动态的连边删边又不得不用LCT
其实,LCT维护一个子树信息并没有那么难
显然本题要维护的是子树siz
我们记tot为子树大小,siz为虚子树大小之和(LCT虚实边)
我们考虑LCT的哪些函数会影响这些东西
首先,upd肯定是要改的,即
void upd() {
tot = siz + 1;
if(ch[0]) tot += ch[0]->tot;
if(ch[1]) tot += ch[1]->tot;
}
注意,左右孩子实际上是splay维护的一条链上的两个点
tot初始为自己的虚子树的和+自己大小1
如果有实儿子,统计总共的大小
接下来rot和splay,显然不会改变边的虚实,所以直接维护即可
然后是access,它会改变很多边的虚实,所以会产生影响
也好维护,让x的siz减掉即将变成实边的虚边的贡献,加上即将变为虚边的实边的贡献即可
makeroot, findroot都没有影响qwq
link,有影响, 因为连了一条虚边,只需加一下贡献即可,加完后upd一下
注意link的不光要makeroot(x),还要把y弄到根上去,这样y就没有祖先了,再加就不会影响了
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 1e5 + 100;
struct LCT {
protected:
struct node {
node *ch[2], *fa;
int siz, rev, tot;
node(int siz = 0, int rev = 0, int tot = 1): siz(siz), rev(rev), tot(tot) { ch[0] = ch[1] = fa = NULL; }
void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }
void dwn() {
if(!rev) return;
if(ch[0]) ch[0]->trn();
if(ch[1]) ch[1]->trn();
rev = 0;
}
void upd() {
tot = siz + 1;
if(ch[0]) tot += ch[0]->tot;
if(ch[1]) tot += ch[1]->tot;
}
bool isr() { return fa->ch[1] == this; }
bool ntr() { return fa && (fa->ch[0] == this || fa->ch[1] == this); }
}pool[maxn];
void rot(node *x) {
node *y = x->fa, *z = y->fa;
bool k = x->isr(); node *w = x->ch[!k];
if(y->ntr()) z->ch[y->isr()] = x;
(x->ch[!k] = y)->ch[k] = w;
(y->fa = x)->fa = z;
if(w) w->fa = y;
y->upd(), x->upd();
}
void splay(node *o) {
static node *st[maxn];
int top;
st[top = 1] = o;
while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;
while(top) st[top--]->dwn();
while(o->ntr()) {
if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
rot(o);
}
}
void access(node *x) {
for(node *y = NULL; x; x = (y = x)->fa) {
splay(x);
if(x->ch[1]) x->siz += x->ch[1]->tot;
x->ch[1] = y;
if(y) x->siz -= y->tot;
x->upd();
}
}
void makeroot(node *o) { access(o), splay(o), o->trn(); }
public:
void link(int l, int r) {
node *x = pool + l, *y = pool + r;
makeroot(x), access(y), splay(y);
(x->fa = y)->siz += x->tot;
y->upd();
}
int query(int l, int r) {
node *x = pool + l, *y = pool + r;
makeroot(x), access(y), splay(y);
return (x->siz + 1) * (y->siz + 1);
}
}s;
int n, m;
char getch() {
char ch;
while(!isalpha(ch = getchar()));
return ch;
}
int main() {
n = in(), m = in();
for(int i = 1; i <= m; i++) {
if(getch() == 'A') s.link(in(), in());
else printf("%d
", s.query(in(), in()));
}
return 0;
}