神经网络中误差反向传播(back propagation)算法的工作原理

神经网络，从大学时候就知道，后面上课的时候老师也讲过，但是感觉从来没有真正掌握，总是似是而非，比较模糊，好像懂，其实并不懂。

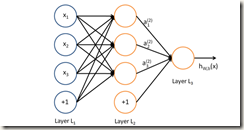
在开始推导之前，需要先做一些准备工作，推导中所使用的神经网络如上图所示。一个神经网络由多个层(layer)构成，每一层有若干个节点(node)，最左边是输入层，中间的层被称为隐含层，最右边是输出层；上一层节点与下一层节点之间，都有边相连，代表上一层某个节点为下一层某个节点贡献的权值。

接下来对推导中使用的符号做一个详细的说明，使推导的过程清晰易懂。我们用代表网络的层数，用代表第层的节点的个数；用/表示第层经过激活函数前/后的节点向量(/代表经过激活函数前/后某个节点的值),根据以上的表示，等于网络的输入,等于网络的输出,也就是上图中的；用表示第层与第层之间的权值形成的矩阵，代表层的节点与层的节点之间的权重(注意这种表示方式),用代表层到层之间的偏置向量。另外，对于激活函数，可以选择不同的形式，这里使用sigmoid函数推导，表达式如下：

之所以使用sigmoid函数，一个很重要的原因就是“mathematical convenience”：sigmoid函数的导数很好计算， 。

对于神经网络各层之间的关系，用简洁的向量矩阵形式来表达如下：

(1)

(2)

根据以上的式子，我们就可以求取网络中每一层各个节点的值了，上述的过程称为前向传播(forward propagation)过程。

通常，网络刚创建好时，我们随机初始化每两层之间的权值矩阵以及偏置向量，但是这样得到的网络，输出与实际的值差距太大，使用神经网络的目的当然是想要网络的输出与实际的值差距尽可能小。随机初始化网络，显然不能满足这个目的，但是如何调整各层之间的权值矩阵以及偏置呢，这并不是一个很简单的问题，下面要推导的反向传播(backward propagation)算法就是解决这个问题的利器。

正式开始推导

通常来说，如果想要得到一个较好的网络，需要有一批已知的训练数据，假设我们现在有一批总共个数据,即。对于每一个样本来说，我们优化的目标为 ：

(3)

对于所有样本来说我们的优化目标为：

(4)

上述优化目标函数，第一项为误差项，第二项称为正则项(也称为weight decay term），用来控制各层权值矩阵的元素大小，防止权值矩阵过大，网络出现过拟合，这和曲线拟合中对参数使用正则道理是一样的，只不过曲线拟合中，参数是向量，这里的参数是一个一个的矩阵，我们使用F范数的平方来约束权重矩阵元素的大小，正则项前面的系数(称为weight decay parameter)用来控制正则项与误差项之间的一个权重。另外，一般来说，不对偏置进行正则。

关于F范数的一点小知识

假设矩阵A是实数矩阵，大小为,其F范数是所有元素的平方和开根号，用公式表示为：

另外关于F范数如何求导，有如下公式：

抽丝剥茧，不断深入

我们目标是求出各层的权值矩阵以及偏置向量，使得优化目标函数取得最小值。根据梯度下降算法，可以求取目标函数对各个参数的偏导，迭代更新参数的值，最终得到最优的参数值(事实上，上述函数是非凸函数，梯度下降并不一定能够得到global optimum，有可能只能得到local optimum，但是实际中得到的结果一般都是比较接近最优结果，在可以接受的范围之内；另外还有更加复杂的方法，譬如加入momentum项，使得目标函数能够跳出local optimum点，从而得到global optimum，这里仅讨论最基本情况，对增加momentum项的情况不予讨论)。

参数的更新公式如下：

(5)

(6)

以上的式子中，称为学习率(learning rate)，用来控制权重和偏置变化的幅度，如果太大，网络的参数收敛速度快，但是可能出现来回震荡的情况，如果太小，网络收敛速度太慢，训练时间长。需要说明，权重矩阵以及偏置向量的学习率可以不一样，根据需要分别设置，实际上，caffe就是这么做的，可以在prototxt里面指定每层的权重以及偏置的学习率。

从上面的公式可以看出，现在的关键变成计算目标函数对权重矩阵以及偏置项各个元素的偏导，结合公式(4)，把公式(5)和(6)中的偏导项展开，得到如下形式：

(7)

(8)

上述公式中，公式(7)后半部分可以参考前面对于矩阵范数求导的公式得到。那么接下的问题就是对于每一个具体的样本，如何求取他们对于权重矩阵以及偏置向量的偏导，也就是如何求以及？这个就要用到我们前面所说的back-propagation的思想了，当我们把一个样本输入到网络，通过前向传播，得到最终的输出，最终输出与实际的值之间有误差，然后我们通过某种有组织有规律的方式把误差一层一层向前传播，这是求解该问题的核心思想。

为了便于推导，再引入变量, 即最终的误差对每一层节点经过激活函数前的变量的偏导数，用它来衡量某一层某个节点对最终误差的一个贡献量。

计算辅助变量的值

对于最后一层(第层)，我们可以很方便的计算该量，详细推导如下：

(9)

上述公式中，，对于其他层也是如此计算，不再赘述。

其他层()的辅助变量，计算就不那么容易了，因为输出误差并不直接和这些层的节点相关，所以我们需要构造关系，利用微积分里面的链式法则(chain rule),具体计算过程如下：

(10)

为了便于书写，公式(10)中,。关于如何由第一行得到第二行，我起初并没有正确得到，后来结合网上给的参考结果，逐渐想通如何计算。求误差对层某个节点的偏导，无法直接求解，因为误差只和最后一层的节点有直接关系，但是如果我们已经知道了误差相对于下一层节点的偏导，而下一层节点和本层直接相关，那么整个链条就可以打通了。通过分配率(譬如我们的目标函数是三个中间函数P,Q,R的函数，而这三个中间函数是自变量x的函数，那么很容易证明下面的式子：，上述公式中第二行的求和符号就是这么来的，起初推导时少了求和符号，只求了误差相对于下一层节点的偏导，没有意识到下一层的每个节点其实与上一层的每个节点都有关系)再加上链式法则，我们就可以很容易求得误差相对于本层的偏导，这就是误差反传的思想。

根据我们前面的定义，公式(10)第二行求和符号里面的第一项，就是。第二项如何显式表达出来呢？这需要利用我们前面说过的关系，具体如下：

(11)

公式(11)中第一个等号与第二个等号后面的式子的推导，参考公式(2)。

有了公式(11)，求解公式(10)第二行第二项偏导就很容易了：

(12)

计算误差相对于矩阵元素和偏置向量元素的偏导

有了以上的铺垫，我们现在可以计算误差相对于矩阵元素以及偏置向量元素的偏导了。

(13)

(14)

向量化表示

对于输出层：

(15)

对于其他层()：

(16)

权重以及偏置更新公式：

(17)

(18)

把所有公式整合在一起

现在我们可以把所有的公式结合在一起，得出最终的参数更新公式了。

step 1. 初始化，对于所有层()，令,,前一项是一个矩阵，后一项是一个向量，分别代表对权重矩阵以及偏置向量的更新量

step 2. 对于一个batch的所有训练样本(for i=1 to m)

a. 使用误差反传计算和

b. 

c. 

step 3. 更新参数

至此，误差反传以及参数更新的全部内容完成！

参考链接

1，斯坦福Andrew Ng的教程，非常清楚易懂，但是省略了具体推导过程

http://ufldl.stanford.edu/wiki/index.php/Backpropagation_Algorithm

2，维基百科，https://en.wikipedia.org/wiki/Backpropagation

3，另外一个很详细清楚的推导，

http://neuralnetworksanddeeplearning.com/chap2.html