洛谷 P2181 对角线
题目
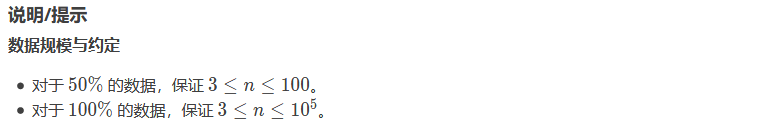
思路分析
- 任何三条对角线都不会交于一点,也就是说,每一个交点仅由两条线相交而得,一个交点对应两条对角线
- 每条对角线对应两个顶点,顶点的个数与多边形的边数相等
- 所以能得出交点与边数的关系,一个交点-->两条对角线-->四个顶点=四条边
- 所以”求交点的个数“可以转化成“求有多少种四个顶点的组合”
- 以六边形为例,从六个顶点中任选四个顶点,使用组合数公式可以得出,一共有(6*5*4*3)/(4*3*2*1)=15种。三边形由于凑不出四个顶点,所以没有交点,符合输出样例的结果
用代码写出来
C/C++
#include<bits/stdc++.h>
int main(){
unsigned long long n;
scanf("%lld",&n);
printf("%lld",n*(n-1)/2*(n-2)/3*(n-3)/4);
return 0;
}
#include<iostream>
using namespace std;
int main(){
unsigned long long n;
cin>>n;
cout<<n*(n-1)/2*(n-2)/3*(n-3)/4;
return 0;
}
-
解析:代码很短,定义一个变量,输入,输出就结束了,但有两个细节
-
用unsigned long long定义变量,因为题目要求3<=n<=100000;在极端情况下,n*(n-1)*(n-2)*(n-3)足足有10^19位数,很容易超出范围,所以必须要用范围尽可能大的数据类型
-
原本是n*(n-1)*(n-2)*(n-3)/24,但由于数据过大,直接算也很容易出错,所以这里把24拆分成2*3*4,变成n*(n-1)/2*(n-2)/3*(n-3)/4,每乘一次就除一下,保证数据尽可能不那么大
还有一点就是必须按照2,3,4的顺序除,以免不能整除。n*(n-1)必定有一个数能被2整除,n*(n-1)*(n-2)必定有一个数能被3整除,n*(n-1)*(n-2)*(n-3)必定有一个数能被4整除。如果调换顺序,先除3或4,那么很有可能不能整除,导致最后结果出错
-
Java
import java.math.BigInteger;
import java.util.Scanner;
public class P2181_对角线 {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
BigInteger n = cin.nextBigInteger();
BigInteger m;
BigInteger o = n;
for (int i = 1; i < 4; i++) {
m = n.subtract(BigInteger.valueOf(i));
o = m.multiply(o);
}
o = o.divide(BigInteger.valueOf(24));
System.out.println(o);
cin.close();
}
}
-
解析:相比C/C++,Java看起来要复杂一点,但其实不难,只有一个重点:用BigInteger定义变量
-
在Java中可以使用BigInteger类来操作大整数,BigInteger是一个类,不能用+,-,*,/来运算,但可以用方法来计算
BigInteger add(BigInteger val)表示+ BigInteger subtract(BigInteger val)表示- BigInteger multiply(BigInteger val)表示* BigInteger divide(BigInteger val)表示- -
还有其他很多操作方法,网上搜一下BigInteger就有
-
最后做除操作的时候没有像C/C++那样分成2,3,4来除,这是因为BigInteger是不可变的任意精度整数,能存储的数据上限很高,网上说是取决于电脑的内存,用在这里是绰绰有余了,而且每次运算的时候都要调用一次方法,分成3次写起来太麻烦了,所以这里就直接除24
-