前言
一星期前用差分约束写了奖学金这道题,在判断impossible的时候,使用了spfa()常用的边数判断法,即更新一个点使用的边数最多应当是n条,在其他点跑的飞快的情况下T了一个点,是一个有环的点,看别人的代码,有的是用dfs判环(这个也有坑下面说),还有的用了双端队列优化。看的我一愣一愣的。由于对spfa及其它判环的原理并不熟悉,我不知道我错在哪里,只有改成上述两种方式才能过。于是我去洛谷寻找spfa判环的模板题,借此了解spfa,在这道题中使用dfs竟然会TLE,难道dfs不是O(m)的吗?什么样的构造会让它Tle?这次的随笔探讨的就是这几个问题:
1. spfa原理是什么?复杂度上界怎么来的?
2. spfa怎么处理环?bfs的两种实现,dfs的一种实现,有向图和无向图的区别?
关于spfa
spfa的原理
-
实现原理
spfa是队列优化的bellman-ford,其实我感觉它就是个普通的bfs(别人的说法SPFA 在形式上和BFS非常类似,不同的是BFS中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本身被改进,于是再次用来改进其它的点,这样反复迭代下去)
具体来说就是:从源点出发,遍历所有出边并入队,再然后再遍历队列中的点,每次进行"松弛操作"(其实我觉得叫"更新操作"或者叫"纠正操作"更容易理解)
记每次队头的点为x,从对列中弹出队头x。
记dis[]为一个点到源点的最短/长路,y为出度点,即edge[i].to,求最短路的时候松弛的条件dis[y]>dis[x]+edge[i].cost,最长路的时候就是dis[y]<dis[x]+edge[i].cost;
当一个点满足这个条件就该更新dis,或者叫纠正dis,如果这个点不在队列中,就把它放入队列。
重复以上步骤直到队列为空。 -
正确性(逻辑原理):
只要联通,bfs必定会遍历全图,每个点第一次被扫到必定更新,必定入队。
队列中每次都会保留待扩展的节点,如果存在dis还能更新,它就会一直更新下去,队列就不会为空,只有所有点都完成更新,队列才会空,保证了正确性。 -
复杂度:
运气好的话,一次遍历就把图更新完了,所有点都不会再扩展,不需要再更新,比如链,或者说更新的比较少。
运气一般的话,因为每次队列中都存在待扩展节点,所以说队头出来之后如果扫到了队列中的点,只可能更新dis而不会再把这个点多展开一次(dfs就可能搜完这次,回溯回来再搜一次),复杂度比dfs优。
(图)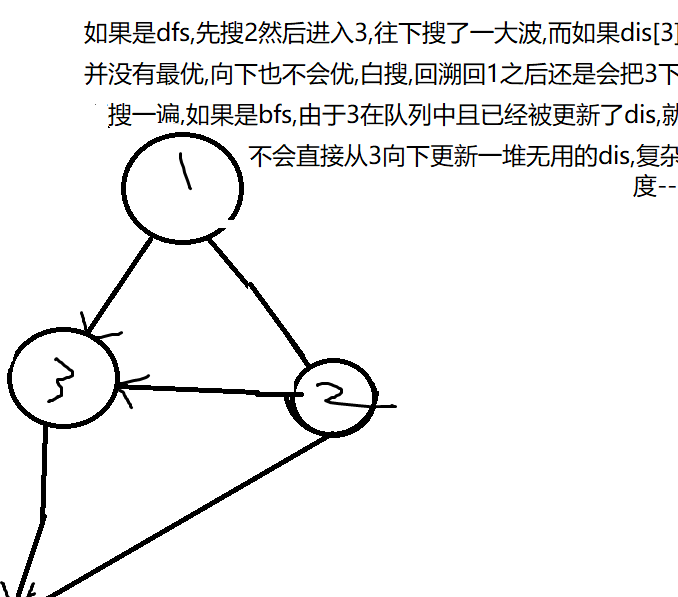
运气很不好,就会达到上界,跨入(O(nm))的级别,怎么达到?
比如说用网格图 来自洛谷某讨论:网格图,10行10000列,纵向边权为1,横向边权随机,亲测普通spfa要跑1分钟
非常可怕的复杂度。
所以对于正权图,跑Dijkstra+heap,稳定log
spfa的环判定
- BFS
- 记录入队次数
用cnt记录每个点入队的次数,如果一个点入队次数大于等于n次,就认为存在负环
为什么?对于bfs,一次bfs中,没有负环的情况下一个点最多入队n次(从源点出连向所有其它点,而所有其他点又指向一个点,每个点正好将这个点更新一次,入队一次),如果说还能再更新一次这个点,那一定是这个点出发跑了一个负环再到达自己,cnt在进入是否
入队的判断中执行。代码如下
- 记录入队次数
bool spfa(){
q.push(1);
vis[1]=1;
while(!q.empty()){
int x=q.front();q.pop();
vis[x]=0;
for(reg int i=head[x];i;i=edge[i].next){
int y=edge[i].to;
if(dis[y]>dis[x]+edge[i].cost){
dis[y]=dis[x]+edge[i].cost;
cnt[y]=cnt[x]+1;
if(cnt[y]>=n) return 1;//包含的边数
if(!vis[y]){
cnt[y]++;
/*if(cnt[y]>=n) return 1; */
q.push(y);
vis[y]=1;
}
}
}
}
return 0;
}
- 记录到达某个点使用的经过的边数
我们可以判断1号点到i号点的最短路径长度是否<n(即经过的点数<=n,没有任何一个点被重复经过)用cnt[y]=cnt[x]+1,cnt[y]>=n来判断,只要进入松弛的判断中就可以执行
代码如下
bool spfa(){
q.push(1);
vis[1]=1;
while(!q.empty()){
int x=q.front();q.pop();
vis[x]=0;
for(reg int i=head[x];i;i=edge[i].next){
int y=edge[i].to;
if(dis[y]>dis[x]+edge[i].cost){
dis[y]=dis[x]+edge[i].cost;
/*cnt[y]=cnt[x]+1;
if(cnt[y]>=n) return 1;//包含的边数 */
if(!vis[y]){
cnt[y]++;
if(cnt[y]>=n) return 1;
q.push(y);
vis[y]=1;
}
}
}
}
return 0;
}
- DFS
dfs版本的思路是在一次搜索中,一旦一个点更新了两次,就说明有负环,为什么?首先搜到一个点两次肯定是有环的,然后第一次更新完了第二次又更新了,除非环的权值是负的,否则不可能更新,于是这样就简单的找到了负环。
对于dfs,有有向图和无向图的区别。如果是一个无向图,vis直接标记,每个非标记点都可以进入,也不用回溯清零,一旦第二次扫描到某个点,就存在环。
如果是一个有向图,扫完一个点的所有出边需要把这个点的标记给去除,不然一个点出发两条路从而到达一个点且无回路,也会被认为是一个环。
dfs一般来说效率是很高的,不过特殊构造下还是会T。并且一次只能处理一个源点出发是否存在环,要求整个图,需要扫描n个点。
代码如下
bool check(int k)
{
vis[k]=1;
for(int i=head[k];i;i=edge[i].next)
{
int y=edge[i].to;
if(dis[k]+edge[i].cost<dis[y]){
dis[y]=edge[i].cost+dis[k];
if(!vis[y])
{
if(check(y))//前面搜到了负环
return 1;
}
else return 1;//一次深搜中搜了一个点两次,则存在负环。
}
}
vis[k]=0;
return 0;
}
二者的取舍
用差分约束并且用bfs判负环导致奖学金这道题T了之后:这判负环必用dfs啊!
用dfs做了洛谷P3385 判负环 之后:这dfs有问题啊。
怎么说呢,如果题目说数据随机,但是可能有环,用dfs判一下环显然会更快,很多时候都是(O(m))的。
如果说没有说数据随机,有几率卡dfs。
如果说题目一看就是得用spfa的,说是有数据存在负环的,那一般不会卡spfa了,但是奖学金这道题就是卡了,不过用了双端队列也就是SLF优化之后就会快很多,直接过了。
总结来说,实际上dfs用的时候需要谨慎,确定有负环的情况下SLF优化还是蛮必要的,这样才更有保障。
另外肯定不能用dfs求最短路,那跟暴力没区别。
如果图没有负权边,那妥妥的Dijkstra+heap。