这里我们提出一个神经网络解决异或问题。
X = np.array([[1,0,0],[1,0,1],[1,1,0],[1,1,1]])
Y = np.array([-1,1,1,-1])
x1 = [0,1] y1 = [1,0] x2 = [0,1] y2 = [0,1]
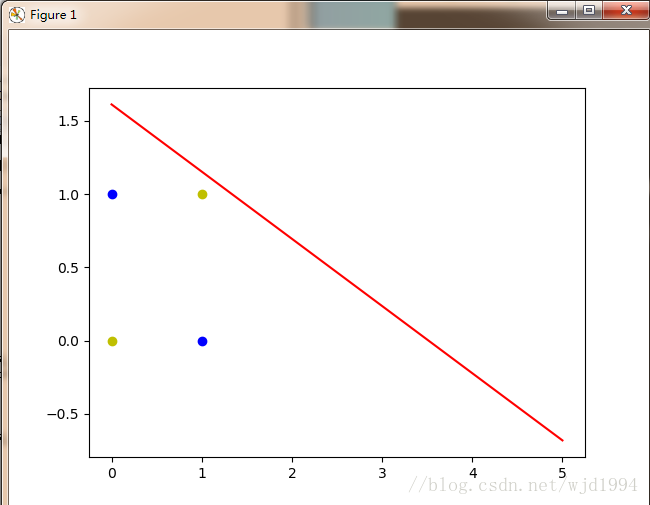
异或问题出现四个点,此时一条直线无法正确地区分出正负样本,于是我们引入线性神经网络
线性神经网络:
线性神经网络于感知器的主要区别在于,感知器的激活函数只能输出两种可能的值,而线性神经网络的输出可以取任意值,其激活函数是线性函数。线性神经网络采用Widrow-Hoff学习规则,即LMS(Least Mean Square)算法来调整网络的权值和偏置。
线性神经网络在结构上与感知器非常相似,只是神经元激活函数不同。在模型训练时把原来的sign函数改为了purelin函数(y=x)。
LMS学习规则:

线性神经网络结构:
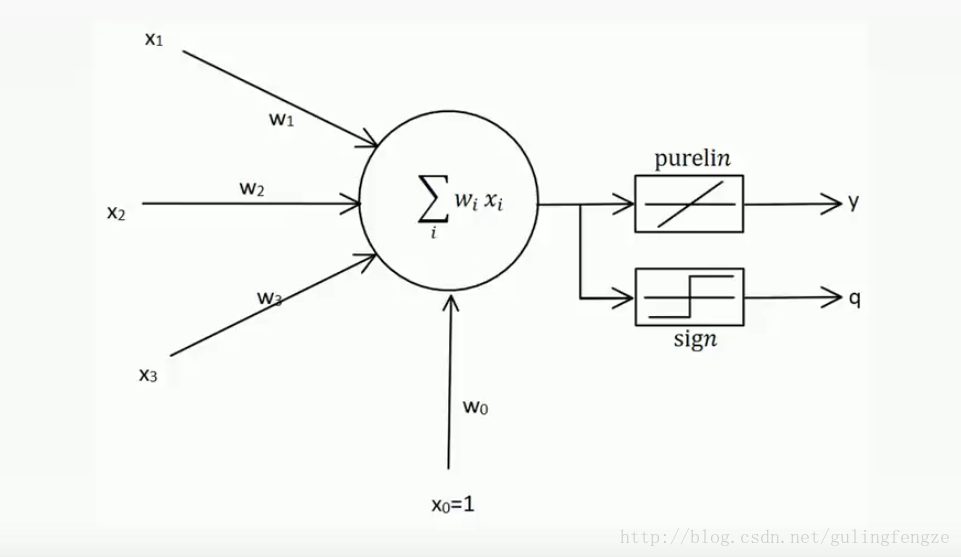
这里我们可以看到线性神经网络结构中有两个激活函数,一个是purelin线性激活函数,一个是感知器里面的sign激活函数。为什么有两个呢?是因为我们训练模型的时候我们可以用purelin线性激活函数,这样我们可以得到一个更好的效果。但是我们输出结果的时候还是要用到sign激活函数,因为要分为-1和1。
Delta学习规则:
1986年,认知心理学家McClelland和Rumelhart在神经网络训练中引入了Delta学习规则,该规则也可以称为连续感知器学习规则。
Delta学习规则是一种利用梯度下降法的一般性的学习规则。
代价函数(损失函数)(Cost Function,Lost Function):

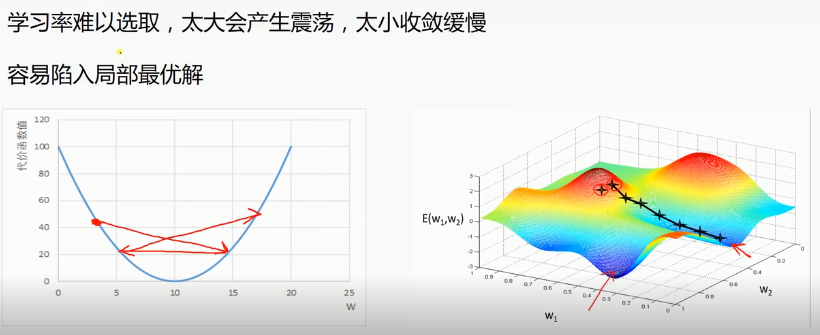
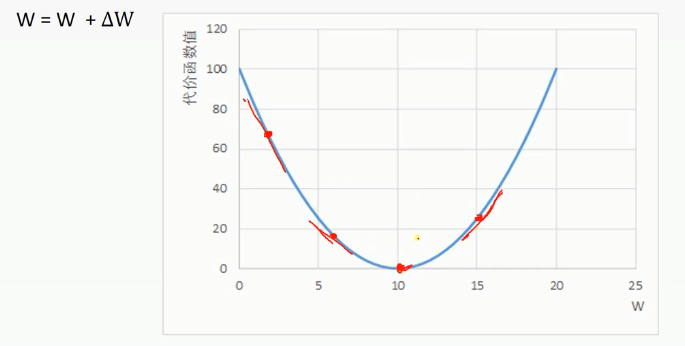
梯度下降法(一维情况):代价函数的值随着权值的改变而改变,改变权值的目的是为了得到最小的代价函数值。假如一个点在左边,△W与负梯度成正比,左边梯度为负数,负梯度即为正,△W与其成正比,所以为正。W=W加上一个正数,所以W就变大,向右移。
梯度下降法(二维情况):红色代表高的地方,蓝色代表低的地方。
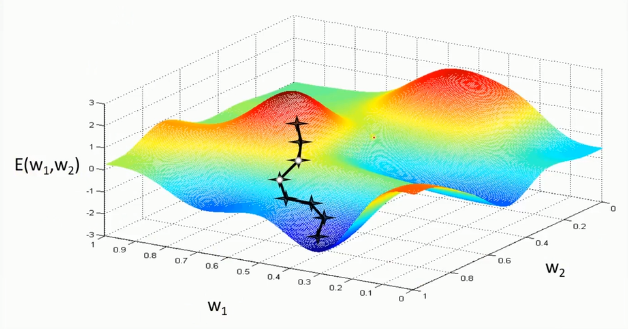
梯度下降法的问题: