统计学习方法：KNN

作者：桂。

时间：2017-04-19  21:20:09

链接：http://www.cnblogs.com/xingshansi/p/6736385.html 

声明：欢迎被转载，不过记得注明出处哦~

---

前言

本文为《统计学习方法》第三章：KNN（k-Nearest Neighbor），主要包括：

　　1）KNN原理及代码实现；

　　2）K-d tree原理；

内容为自己的学习记录，其中多有借鉴他人的地方，最后一并给出链接。

一、KNN原理及代码实现

KNN对应算法流程：

 其实就是在指定准则下，最近的K个决定了自身的类别。

• LP距离

p=2时为欧式距离（Euclidean distance），p=1为曼哈顿距离（Manhattan distance），p=∞对应最大值。

• K值选择

K通常选较小的数值，且通过交叉验证来寻优。

试着写了三种距离下的KNN，给出主要代码：

function resultLabel = knn(test,data,labels,k,flag)
%%
%   test：test database
%   data：train database
%   labels：train data labels
%   flag: distance criteria selection.
%     'E':Euclid Distance.
%     'M':Manhanttan distance.
%     'C':Cosine similarity.
%%
resultLabel=zeros(1,size(test,1));
dats.f=flag;
switch flag
    case 'C'
        Ifg='descend';
    otherwise
        Ifg='ascend';
end
for i=1:size(test,1)
    dats.tes=test(i,:);
    dats.tra=data;
    distanceMat =distmode(dats);
    [B , IX] = sort(distanceMat,Ifg);
    len = min(k,length(B));
    resultLabel(1,i) = mode(labels(IX(1:len)));
end
end

　dismode.m:　

function distanceMat =distmode(dats)
%distance calculation.
%%
% dats.tra:train database;
% dats.tes:test database;
% dats.f: distance flag;
%%
switch dats.f
    case 'E'%Euclidean distance
        p=2;
        datarow = size(dats.tra,1);
        diffMat = abs(repmat(dats.tes,[datarow,1]) - dats.tra) ;
        distanceMat=(sum(diffMat.^p,2)).^1/p;
    case 'M'%Manhanttan distance
        p=1;
        datarow = size(dats.tra,1);
        diffMat = abs(repmat(dats.tes,[datarow,1]) - dats.tra) ;
        distanceMat=(sum(diffMat.^p,2)).^1/p;
    case 'C'%Cosine similarity
        datarow = size(dats.tra,1);
        tesMat = repmat(dats.tes,[datarow,1]) ;
        diffup=sum(tesMat.*dats.tra,2);
        diffdown=sqrt(sum(tesMat.*tesMat,2)).*sqrt(sum(dats.tra.*dats.tra,2));
        distanceMat=diffup./diffdown;
end

　　

二、K-d tree原理

KNN方法对于一个测试数据，需要与所有训练样本比对，再排序寻K个最优，现在换一个思路：如果在比对之前，就按某种规则排序（即构成一个二叉搜索树），这样一来，对于一个新的数据点，只要在前后寻K个最优即可，这样就提高了搜索的效率。

给出构造平衡kd树的算法：

以一个例子分析该思路，给定一个数据集：

对应思路：

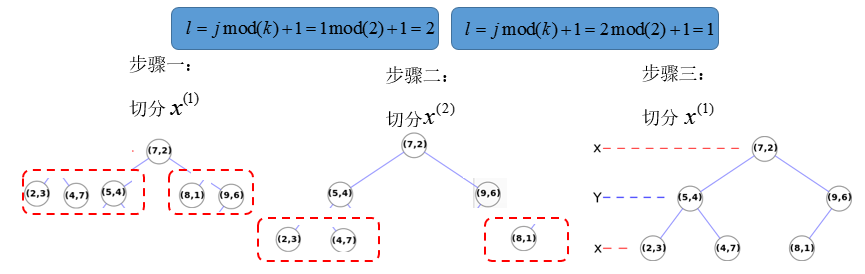
步骤一：x^（1）的中位数：7，对应数据{7，2};按小于/大于分左右；

步骤二：1mod2+1=2，对x⁽²⁾的中位数，对第二层进行划分，左边中位数为5，右边中位数为9，依次划分；

步骤三：2mod2+1=1，对x^（1）的第三层进行划分，结束，对应效果图：

为什么KD树可以这么构造？这也容易理解，对于一个数据点（x,y），距离公式为，单单比较x是不够的，如果对x按大小已经切分，下一步怎么做？再按y进行切分，这样距离大小就被细化，查找范围进一步缩小，x切完y切，如果是三维，y切完z再切，对应数学表达就是。 

构造出了Kd tree之后，如何借助它解决kNN问题呢？

给出搜索kd tree的算法：

 给出下图，现有（2，5）这个点，希望找出最近的K=3 个点：

分析步骤：

步骤一：包含（2,5）的叶节点,发现落在（4，7）节点区域内，（4，7）为当前最近点；

步骤二：检查（4，7）对应父节点（5，4）的另一个子节点（2，3）,发现距离（2，5）更近，（2，5）记为当前最近点；

步骤三：向上回退到（5，4）,此时（5，4）时子节点，其父节点为（7，2）,依次类推。

具体如下图所示：

为什么KD树可以这么搜索？对应节点（右图）可以看出搜索按层回溯，对应左图就是先上下搜索，再往右推进。这样理解就比较直观，因为距离是越来越大的。

完成寻最优以后，最简单的办法是删除节点，重复寻最优，当然也可以存储不同结果，在少量样本中挑出K个最优

 同理，对于三维数据，可以依次类推：

给出Kd tree的测试代码的效果图，code对应链接点击这里：

参考：

• http://blog.csdn.net/silangquan/article/details/41483689
• 李航《统计学习方法》
• https://en.wikipedia.org/wiki/K-d_tree