作者：桂。
时间：2017-04-16 11:53:22
链接：http://www.cnblogs.com/xingshansi/p/6718503.html
前言
今天开始学习李航的《统计学习方法》，考虑到之前看《自适应滤波》，写的过于琐碎，拓展也略显啰嗦，这次的学习笔记只记录书籍有关的内容。前段时间朋友送了一本《机器学习实战》，想着借此增加点文中算法的代码实现，以加深对内容的理解。本文梳理书本第二章：感知机(Perceptron)。
1）原理介绍
2）代码实现
内容为自己学习记录，如果不对的地方，麻烦各位提醒一下。
一、原理介绍
A-感知机模型
感知机的结构为：
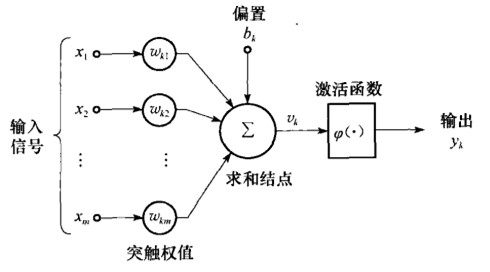
可以看出它是神经网络的理论基础。感知机的前提是假设数据线性可分，输入空间为：
，输出空间：
，根据上面的结构图，可以写出映射关系：
其中
是模型参数，w叫做权值/权重（weight）。b叫做偏置（bias）.感知器的理论解释如下图：
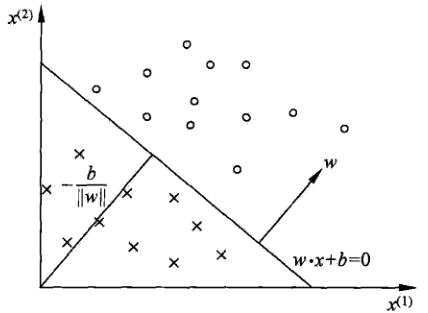
求解的超平面将数据分为正/负两部分。
B-准则函数
对于线性可分的数据集
，其中
如果存在超平面
能够将数据分为正负两侧，则数据集是线性可分数据集，否则是线性不可分数据集。感知器的前提认为数据集线性可分。
感知器的学习角度是：考虑所有点到分离面的总距离。
空间一点$x_0$到分离面的距离可以写为：
，从而所有点到超平面的距离为：
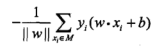
因为是考虑分离面，而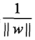
不影响最终求解，从而对其忽略，得到感知器准则函数：
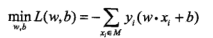
C-算法求解
对于任意一个样本点，求梯度：
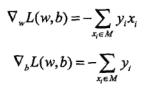
这是批量梯度下降法.文中没有利用这种优化方法，而是每次随机取一个点，即采用随机梯度下降法。最简单的是利用固定步长，迭代优化：
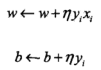
给出完整的算法流程：
收敛性证明用了Novikoff定理，这里不再列出了，对应原文证明点击这里。
D-对偶形式
再次给出原始问题的迭代：
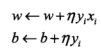
且
其中$n_i$为误分的样本数，假设正确分类，可以认为$alpha_i=0$，上式可以重新写成：
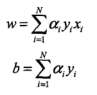
可以看出，当遇见误分的样本时，$n_i$数量增加1，即
b的更新迭代形式不变。从而得到对偶形式的算法流程：
由于对偶问题中，数据仅仅以内积形式出现，因此可以提前计算出来，迭代优化时直接调用，内积构成的矩阵，就是Gram矩阵：
E-对偶形式的核函数转化
对偶形式中
，$x_ix_j$成对出现，可以利用核函数（${phi left( {{x_i}}
ight)}$为核函数）的变换：
这就是核感知器（Kernel percettron）。
二、代码实现
A-算法2.1（原始形式）
上面分析提到，其实优化的时候，理论上利用批量梯度下降法，随机梯度下降法都应该是可行的。给出随机梯度下降法代码：
%%随机梯度下降
clc;clear all;close all;
%percertron
N = 100;
X = [randn(N,2)+2*ones(N,2);...
randn(N,2)-2*ones(N,2)];
figure;
subplot 121
label = [ones(N,1);-ones(N,1)];
plot(X(label==1,1),X(label==1,2),'b.');hold on;
plot(X(label==-1,1),X(label==-1,2),'r.');hold on;
%初始化
W=rand(1,size(X,2));
b=rand(1);
T=100;%迭代次数
eta = 1;
for epochs=1:T
epochs
tag = 0;
for j=1:size(X,1)
if (label(j)*(W*X(j,:)'+b))<=0
W=W+eta*label(j)*X(j,:);
b=b+eta*label(j);
if min (label'.*(W*X'+b))>0
tag = 1;
break;
end
end
end
if tag ==1
break;
end
end
subplot 122
plot(X(label==1,1),X(label==1,2),'b.');hold on;
plot(X(label==-1,1),X(label==-1,2),'r.');hold on;
x = -5:.1:5;
y = -W(1)/W(2)*x-b/W(2);
plot(x,y,'k','linewidth',2);
结果图：
如果想采用批量梯度下降法，将迭代部分的代码修改为：
for j=1:size(X,1)
if min(label(j)*(W*X'+b))<=0
W=W+eta*label'*X;
b=b+eta*ones(1,2*N)*label;
if min (label'.*(W*X'+b))>0
tag = 1;
break;
end
end
end
这样就完成了批量梯度下降算法的求解。
B-算法2.2（对偶形式）
给出代码：
%%对偶方法求解
clc;clear all;close all;
%percertron
N = 100;
X = [randn(N,2)+2*ones(N,2);...
randn(N,2)-2*ones(N,2)];
Gram = X*X';
figure;
subplot 121
label = [ones(N,1);-ones(N,1)];
plot(X(label==1,1),X(label==1,2),'b.');hold on;
plot(X(label==-1,1),X(label==-1,2),'r.');hold on;
title('原数据')
%初始化
alpha=rand(1,size(X,1));
b=rand(1);
T=1000;%迭代次数
eta = 0.5;
for epochs=1:T
epochs
tag = 0;
for j=1:size(X,1)
if (label(j)*((alpha'.*label)'*Gram(:,j)+b))<=0
alpha=alpha+eta;
b=b+eta*label(j);
end
end
end
predict = sign((alpha.*label')*Gram'+b)';
subplot 122
plot(X(predict==1,1),X(predict==1,2),'b.');hold on;
plot(X(predict==-1,1),X(predict==-1,2),'r.');hold on;
title('分类数据')
对应结果图：
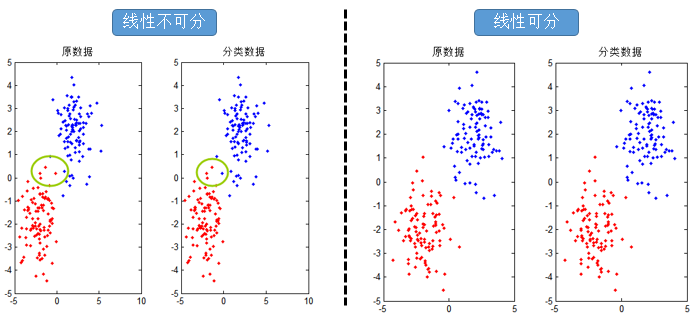
可以看出线性可分时，分里面决定的数据与原始数据一致，而当线性不可分的时候，就出现了错误，线性不可分怎么处理呢？这就是核函数的作用了。
C-对偶形式的核函数
为了直观，给出四个点的数据：
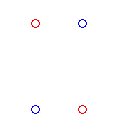
可以看出这样的四个数据点是线性不可分的，常用核函数有：
1）高斯核函数K(x,xi) =exp(-||x-xi||2/2σ2；
2）多项式核函数K(x,xi)=(x·xi+1)^d, d=1,2,…,N；
3）感知器核函数K(x,xi) =tanh(βxi+b)；
4）样条核函数K(x,xi) = B2n+1(x-xi)。
这里以高斯核为例，给出代码：
%%kernel
clc;clear all;close all;
%percertron
gamma = 1;
X = [0 1 1 0;0 1 0 1]';
Gram = exp(-dist(X,X').^2*gamma);
% Gram = X*X';
figure;
subplot 121
label = [ones(2,1);-ones(2,1)];
plot(X(label==1,1),X(label==1,2),'bo');hold on;
plot(X(label==-1,1),X(label==-1,2),'ro');hold on;
title('原数据');
axis([-2 2 -2 2]);
%初始化
alpha=rand(1,size(X,1));
b=rand(1);
T=1000;%迭代次数
eta = 1;
for epochs=1:T
epochs
for j=1:size(X,1)
if (label(j)*((alpha'.*label)'*Gram(:,j)+b))<=0
alpha=alpha+eta;
b=b+eta*label(j);
end
end
end
predict = sign((alpha.*label')*Gram'+b)';
subplot 122
plot(X(predict==1,1),X(predict==1,2),'bo');hold on;
plot(X(predict==-1,1),X(predict==-1,2),'ro');hold on;
axis([-2 2 -2 2]);
title('分类数据')
从结果可以看出，核函数可以解决非线性的困难。
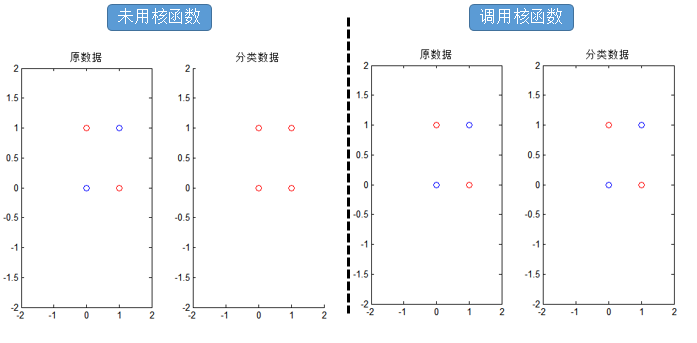
参考：
李航《统计学习方法》.