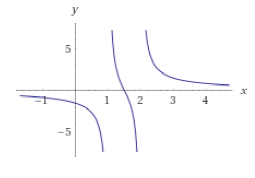
探讨函数$f(x)=dfrac{1}{x-a}+dfrac{1}{x-b}$其中$a<b$的几个性质
分析:
对称性:关于$(dfrac{a+b}{2},0)$证明提示:$f(x)+f(a+b-x)=0$且定义域关于$(dfrac{a+b}{2},0)$对称
单调性:单调递减区间$(-infty,a),(a,b),(b,+infty)$,证明提示:用单调性的定义
渐进性:$limlimits_{x
ightarrow-infty}f(x)=0$;$limlimits_{x
ightarrow+infty}f(x)=0$;
$limlimits_{x
ightarrow a^+}f(x)=+infty$;$limlimits_{x
ightarrow a^-}f(x)=-infty$
$limlimits_{x
ightarrow b^+}f(x)=+infty$;$limlimits_{x
ightarrow b^-}f(x)=-infty$
最后提供一张$a=1,b=2$时的图.