Orz。。。
不吐槽这次比赛了。
。。
还是太弱了。
。
There are n children in Jzzhu's school. Jzzhu is going to give some candies to them. Let's number all the children from 1 to n. The i-th child wants to get at least ai candies.
Jzzhu asks children to line up. Initially, the i-th child stands at the i-th place of the line. Then Jzzhu start distribution of the candies. He follows the algorithm:
- Give m candies to the first child of the line.
- If this child still haven't got enough candies, then the child goes to the end of the line, else the child go home.
- Repeat the first two steps while the line is not empty.
Consider all the children in the order they go home. Jzzhu wants to know, which child will be the last in this order?
The first line contains two integers n, m (1 ≤ n ≤ 100; 1 ≤ m ≤ 100). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 100).
Output a single integer, representing the number of the last child.
5 2 1 3 1 4 2
4
6 4 1 1 2 2 3 3
6
Let's consider the first sample.
Firstly child 1 gets 2 candies and go home. Then child 2 gets 2 candies and go to the end of the line. Currently the line looks like [3, 4, 5, 2] (indices of the children in order of the line). Then child 3 gets 2 candies and go home, and then child 4 gets 2 candies and goes to the end of the line. Currently the line looks like [5, 2, 4]. Then child 5 gets 2 candies and goes home. Then child 2 gets two candies and goes home, and finally child 4 gets 2 candies and goes home.
Child 4 is the last one who goes home.
这道题也就这样。
。
。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
#define INF 0x3f3f3f3f
using namespace std;
int main()
{
int n, m;
int ans = 0, t = 0, a;
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> a;
if (i == 0 || (a+m-1)/m >= t)
{
ans = i+1;
t = (a+m-1)/m;
}
}
cout << ans << endl;
return 0;
}
还实用队列写的。。
这个非常方便。。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 10;
int n, m;
struct node
{
int id, cd;
};
int main()
{
int i, j;
scanf("%d%d", &n, &m);
queue<node> q;
for(i=1; i<=n; ++i)
{
scanf("%d", &j);
node t;
t.id = i; t.cd = j;
q.push(t);
}
node cur;
while(!q.empty())
{
cur = q.front(); q.pop();
if(cur.cd >m)
{
cur.cd -= m;
q.push(cur);
}
}
printf("%d
", cur.id);
return 0;
}
Jzzhu has invented a kind of sequences, they meet the following property:
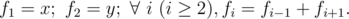
You are given x and y, please calculate fn modulo 1000000007 (109 + 7).
The first line contains two integers x and y (|x|, |y| ≤ 109). The second line contains a single integer n (1 ≤ n ≤ 2·109).
Output a single integer representing fn modulo 1000000007 (109 + 7).
2 3 3
1
0 -1 2
1000000006
In the first sample, f2 = f1 + f3, 3 = 2 + f3, f3 = 1.
In the second sample, f2 = - 1; - 1 modulo (109 + 7) equals (109 + 6).
B题被人HACK了。。。
原来没考虑好为-1的情况。。淡淡的忧桑。。。。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
#define INF 1000000007
using namespace std;
int main()
{
int x, y;
cin>>x>>y;
int n;
cin>>n;
n %= 6; //6次一循环
int a[10];
a[1]=(x+INF) % INF;
a[2]=(y+INF) % INF;
a[3]=(a[2]-a[1]+INF) % INF;
a[4]=(-x+INF) % INF;
a[5]=(-y+INF) % INF;
a[0]=(a[1]-a[2]+INF) % INF;
n = n%6;
cout<<a[n]<<endl;
return 0;
}
Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactlyk cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
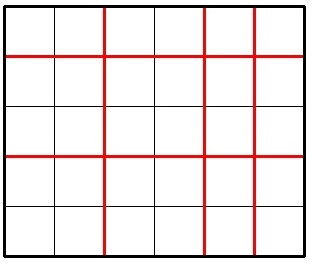
3 4 1
6
6 4 2
8
2 3 4
-1
In the first sample, Jzzhu can cut the chocolate following the picture below:
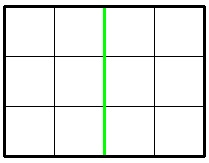
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
#define INF 0x3f3f3f3f
using namespace std;
long long int n, m, k;
long long int i;
int main()
{
cin >> n >> m >>k;
if( k>n+m-2 )
{
cout << "-1"<<endl;
return 0;
}
long long int a=0, b=0;
for(i=0; i<2; swap(n,m))
{
if( k<n-1 )
a = (n/(k+1))*m;
else
a = m/(k-n+2);
if( a>=b )
b = a;
i++;
}
cout << b << endl;
return 0;
}