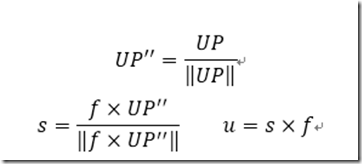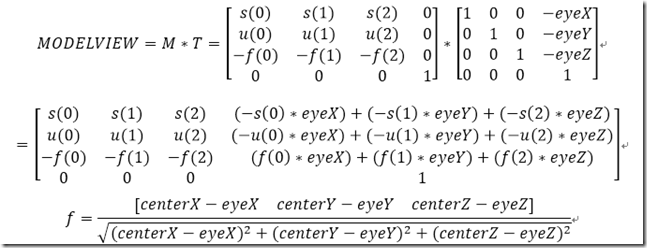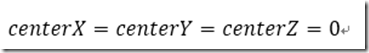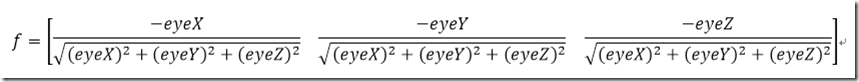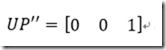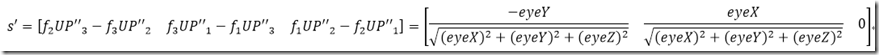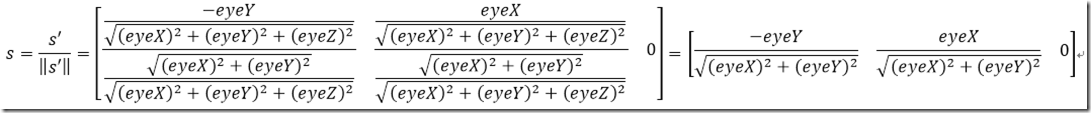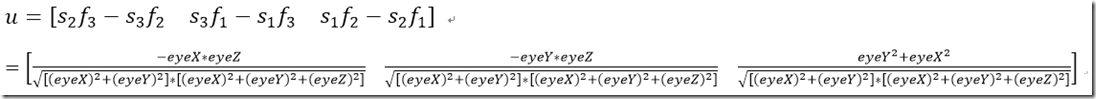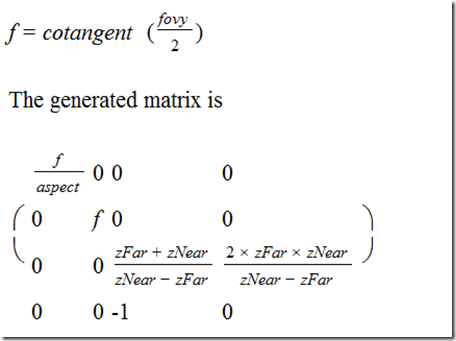有时候我们需要手动计算三维点对应的二维坐标,下面的矩阵公式就是模拟了一遍三维图形的流程。这里已假设读者具备了图形学的基础知识,比如矩阵乘法代表的三维变换,放射变换;还有齐次坐标等。
这里不考虑模型自身的旋转平移缩放等,即假设模型三维坐标已知。有坐标:
模型视图变换矩阵:
void APIENTRY gluLookAt (
GLdouble eyex,
GLdouble eyey,
GLdouble eyez,
GLdouble centerx,
GLdouble centery,
GLdouble centerz,
GLdouble upx,
GLdouble upy,
GLdouble upz);
这个矩阵可以参考OpenGL的官网:http://www.opengl.org/sdk/docs/man2/
最好用IE或者firefox打开,chrome无法打开公式插件。
这里列出几点需要注意的,官网上没有注意。
这是官网上的截图,其中![]() 表示2-范数。另外向量s和u均需要像f和UP一样用2-范数作为商归一化。最终计算一个矩阵,这里热身一下,给出所有推导过程:
表示2-范数。另外向量s和u均需要像f和UP一样用2-范数作为商归一化。最终计算一个矩阵,这里热身一下,给出所有推导过程:
一点理解:f表示视线向量,UP’’表示摄影机朝向的向量,但是可以知道,如果视线向量定了,其实摄影机的角度也就定了,但是摄影机可以绕着以视线方向作为轴进行旋转,所以UP’’向量就是为了固定摄像机用的。其中叉积有这样的一个性质:
所以如果f与UP’’如果是垂直的,那么就不需要进行归一化了,因为f和UP’’的长度均为1,他们如果垂直,叉积的长度也为1。但是我们编程中经常使用沿着笛卡尔坐标轴的向量表示摄影机的朝向,所以这里还是需要进行归一化的。s归一化后,s与f是垂直的,所以u并不需要再归一化。
在实际情况中,我们总是往简单的方向设定:
则
并且有
那么
再归一化s’
因此
最终矩阵:
投影矩阵:
void APIENTRY gluPerspective (
GLdouble fovy,
GLdouble aspect,
GLdouble zNear,
GLdouble zFar);
同样,可以参考官网上API:http://www.opengl.org/sdk/docs/man2/
视口变换矩阵:
WINGDIAPI void APIENTRY glViewport (GLint x, GLint y, GLsizei width, GLsizei height);
可以把上式写成矩阵的形式。
三维坐标经过上诉三个变换,即可变换成为最终二位坐标点。最后仍需注意的是,变换后的坐标原点为窗口左下角,一般图像处理时均是左上角为原点,对Y坐标进行一次变换即可。
Y’=Height-Y