时间复杂度

算法分析

　　一个算法的效率一般以执行时间来衡量。度量一段程序的执行时间有以下两种方式：

　　事后统计：对一段程序多次执行，统计执行时间。

　　事前分析估算：对算法程序的分析，估算算法大概执行时间。当然，估算的时间并不是一个具体的值，而是一个与n（n表示问题规模）有关的函数。

　　事后统计方式的缺陷很明显：一是需要等待程序执行，若程序过大，执行时间会较长。二是执行时间除了和算法有关之外，还与计算机的硬件、软件等环境因素相关，统计出来的数据不一定准确。所以一般使用事前分析估算算法的执行时间长短。

时间复杂度

　　一个语句的频度是指该语句重复执行的次数。一个算法的时间频度指的是算法中最大的语句频度，用T(n)表示。

　　例如，计算从1加到n的和：

public static int sum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) sum += i;
    return sum;
}

　　对于这段程序而言，其时间频度T(n) = n + 1（语句“i <= n”的频度最大，重复执行了n + 1次）。

public static int sum(int n) {
    return (1 + n) * n / 2;
}

　　对于这段程序而言，其时间频度T(n) = 1。

　　所以，两段程序的执行结果相同，但明显地第二个程序的时间频度比第一个小，其执行效率就比第一个高。

　　程序规模较小还可以用时间频度衡量，而程序规模大时，一般不再以时间频度衡量，而是以时间复杂度衡量。

　　时间复杂度O(f(n))与时间频度T(n)的关系为：

　　

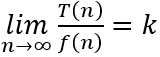
　　其中，k为常数。

　　此时可以记为：T(n)=O(f(n))。

　　例如，算法a的时间频度T(n) = 4n³ + 3n² + 2n，算法b的时间频度T(n) = n³ + n²，如果按时间频度衡量的话，算法b的效率更高；但是a、b的时间复杂度都是O(n³)，所以算法a和b的效率相差不大。

　　常见的时间复杂度类型从低到高依次是：常数阶、对数阶、线性阶、线性对数阶、k次方阶、指数阶和阶乘阶。

常数阶

　　常数阶的算法指的是时间复杂度为O(1)的算法。例如，算法程序不包含循环结构：

public static int sum(int n) {
    return (1 + n) * n / 2;
}

对数阶

　　对数阶的算法指的是时间复杂度为O(log n)的算法。例如，算法程序只有一层循环，循环变量翻倍迭代：

public static int sum(int n) {
    int sum = 0;
    for (int i = 1; i < 10; i *= 2) sum += i;
    return sum;
}

线性阶

　　线性阶的算法指的是时间复杂度为O(n)的算法。例如，算法程序只有一层循环，循环变量自增迭代：

public static int sum(int n) {
    int sum = 0;
    for (int i = 1; i < 10; i ++) sum += i;
    return sum;
}

线性对数阶

　　线性对数阶的算法指的是时间复杂度为O(n log n)的算法。例如，算法程序有两层循环，外循环的循环变量自增迭代，内循环的循环变量翻倍迭代：

public static int sum(int n) {
    int sum = 0;
    for (int i = 1; i < 10; i ++) 
        for (int j = 1; j < 10; j *= 2) 
            sum += i * j;
    return sum;
}

k次方阶

　　k次方阶的算法指的是时间复杂度为O(n^k)（k > 1）的算法。例如，立方阶的算法程序有三层循环，且三层循环的循环变量都是自增迭代：

public static int sum(int n) {
    int sum = 0;
    for (int i = 1; i < 10; i++) 
        for (int j = 1; j < 10; j++) 
            for (int k = 1; k < 10; k++) 
                sum += i * j * k;
    return sum;
}

指数阶

　　指数阶的算法指的是时间复杂度为O(aⁿ)（a > 1）的算法。

阶乘阶

　　阶乘阶的算法指的是时间复杂度为O(n!)的算法。