【转】
——————————————————————————
——————————————————————————
《算法导论》练习18.3-2: 请写出B-TREE-DELETE的伪代码。
与插入情况相对称,除了根结点外(根结点个数不能少于1),B树的关键字数不能少于t-1个。对于简单删除情况,如果我们定位到关键字处在某个结点中,如果这个结点中关键字个数恰好是t-1个,如果直接删除这个关键字,就会违反B树规则。
此时,需要考虑两种处理方案:
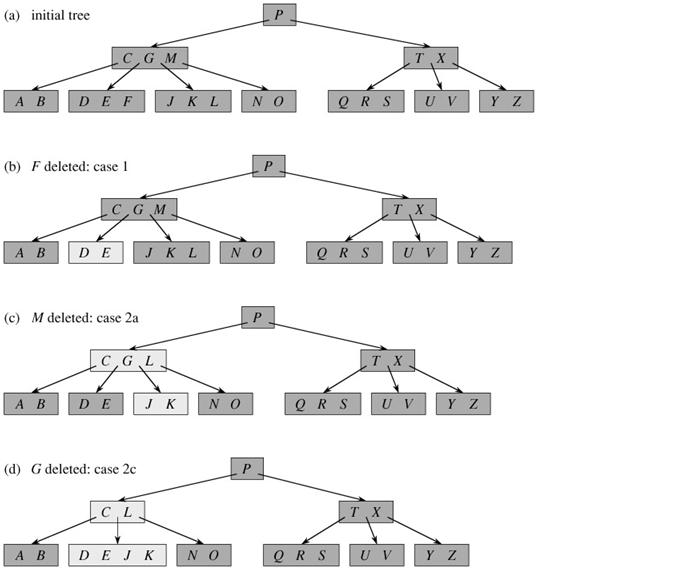
1)把这个结点与其相邻结点合并,合并时需要把父结点的一个关键字加进来,除非相邻的那个结点的关键字数也是t-1个,否则,合并后会超出2t-1的限制,同样违反B树规则。而且,因为从父结点拉下一个关键字,导致父结点的关键字数少1,如果原来父结点关键字数是t-1,那么父结点违反B树规则,这种情况下,必须进行回溯处理。(对于下图(a)初始树,删除结点Z就会出现这种情况)
2)从相邻结点借一个关键字过来,这种情况要求,相邻结点必须有多于t-1个关键字,借的过程中,需要转经父结点,否则违反B树规则。
为了避免回溯,要求我们在从树根向下搜索关键字的过程中,凡是遇到途经的结点,如果该结点的关键字数是t-1,则我们需要想办法从其他地方搞个关键字过来,使得该结点的关键字数至少为t。
搞,也是从相邻结点搞,如果相邻结点有的话,当然,也要经过父结点进行周转。如果没有,就说明相邻结点的关键字个数也是t-1,这种情况,直接对该结点与其相邻结点进行合并,以满足要求。
B树的结点的合并基于如下情况调用:内结点x的第i个子结点y和第i+1个子结点z的关键字数都是t-1,此时需要把内结点x的第i个关键字下移与y和z的合并,形成一个结点y。
B树中结点的合并:
B-TREE-MERGE-CHILD(x, i, y,z)
1 n[y] ← 2t -1
2 for j ← t +1 to 2t -1
3 do keyj[y] ← keyj-t[z]
4 keyt[y] ← keyi[x]
5 if not leaf[y]
6 then for j ← t +1 to 2t -1
7 do cj[y] ← cj-t[z]
8 for j ← i +1 to n[x]
9 do cj[x] ← cj+1[x]
10 n[x] ← n[x] -1
11 FREE-NODE(z)
12 DISK-WRITE(y)
13 DISK-WRITE(z)
14 DISK-WRITE(x)
B树的删除:
B-TREE-DELETE(T,k)
1 r ← root[T]
2 if n[r] = 1
3 then DISK_READ(c1[r])
4 DISK_READ(c2[r])
5 y ←c1[r]
6 z ←c2[r]
7 if n[y] = n[z] = t-1 ▹ Cases 2c or 3b
8 then B-TREE-MERGE-CHILD(r, 1, y, z)
9 root[T] ← y
10 FREE-NODE(r)
11 B-TREE-DELETE-NONONE(y, k)
12 else B-TREE-DELETE-NONONE (r, k)
13 else B-TREE-DELETE-NONONE (r, k)
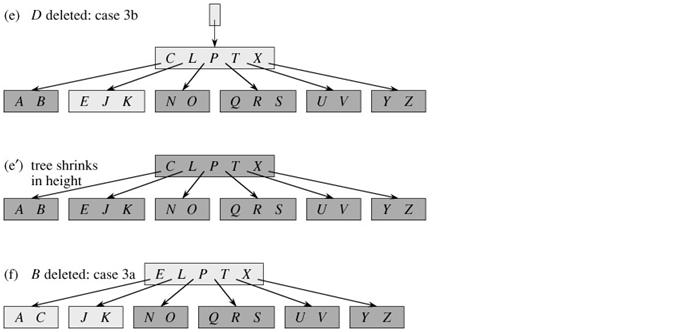
考虑到根结点的特殊性,对根结点为1,并且两个子结点都是t-1的情况进行了特殊的处理:
先对两个子结点进行合并,然后把原来的根删除,把树根指向合并后的子结点y。
这样B树的高度就减少了1。这也是B树高度唯一会减少的情况。
除了这种情况以外,就直接调用子过程B-TREE-DELETE-NONONE (x, k)。
B-TREE-DELETE-NONONE (x, k)
1 i ← 1
2 if leaf[x] ▹ Cases 1
3 then while i <= n[x] and k > keyi[x]
4 do i ← i + 1
5 if k = keyi[x]
6 then for j ← i+1 to n[x]
7 do keyj-1[x] ←keyj[x]
8 n[x] ← n[x] - 1
9 DISK-WRITE(x)
10 else error:”the key does not exist”
11 else while i <= n[x] and k > keyi[x]
12 do i ← i + 1
13 DISK-READ(ci[x])
14 y ←ci[x]
15 if i <= n[x]
16 then DISK-READ(ci+1[x])
17 z ←ci+1[x]
18 if k = keyi[x] ▹ Cases 2
19 then if n[y] > t-1 ▹ Cases 2a
20 then k′←B-TREE-SEARCH-PREDECESSOR(y)
21 B-TREE-DELETE-NONONE (y, k′)
22 keyi[x] ←k′
23 else if n[z] > t-1 ▹ Cases 2b
24 then k′←B-TREE-SEARCH-SUCCESSOR (z)
25 B-TREE-DELETE-NONONE (z, k′)
26 keyi[x] ←k′
27 else B-TREE-MERGE-CHILD(x, i, y, z)▹ Cases 2c
28 B-TREE-DELETE-NONONE (y, k)
29 else ▹ Cases 3
30 if i >1
31 then DISK-READ(ci-1[x])
32 p ←ci-1[x]
33 if n[y] = t-1
34 then if i>1 and n[p] >t-1 ▹ Cases 3a
35 then B-TREE-SHIFT-TO-RIGHT-CHILD(x,i,p,y)
36 else if i <= n[x] and n[z] > t-1 ▹ Cases 3a
37 then B-TREE-SHIFT-TO-LEFT-CHILD(x,i,y,z)
38 else if i>1 ▹ Cases 3b
39 then B-TREE-MERGE-CHILD(x, i, p, y)
40 y ← p
41 else B-TREE-MERGE-CHILD(x, i, y, z)▹ Cases 3b
42 B-TREE-DELETE-NONONE (y, k)
查找前驱
B-TREE-SEARCH-PREDECESSOR(y)
1 x ← y
2 i ← n[x]
3 while not leaf[x]
4 do DISK_READ(ci+1[x])
5 x ←ci+1[x]
6 i ← n[x]
7 return keyi[x]
查找后继
B-TREE-SEARCH-SUCCESSOR (z)
1 x ← z
2 while not leaf[x]
3 do DISK_READ(c1[x])
4 x ←c1[x]
5 return key1[x]
转移到右边的子结点
B-TREE-SHIFT-TO-RIGHT-CHILD(x,i,y,z)
1 n[z] ← n[z] +1
2 j ← n[z]
3 while j > 1
4 do keyj[z] ←keyj-1[z]
5 j ← j -1
6 key1[z] ←keyi[x]
7 keyi[x] ←keyn[y][y]
8 if not leaf[z]
9 then j ← n[z]
10 while j > 0
11 do cj+1[z] ←cj[z]
12 j ← j -1
13 c1[z] ←cn[y]+1[y]
14 n[y] ← n[y] -1
15 DISK-WRITE(y)
16 DISK-WRITE(z)
17 DISK-WRITE(x)
转移到左边的子结点
B-TREE-SHIFT-TO-LEFT-CHILD(x,i,y,z)
1 n[y] ← n[y] +1
2 keyn[y][y] ← keyi[x]
3 keyi[x] ←key1[z]
4 n[z] ← n[z] -1
5 j ← 1
6 while j <= n[z]
7 do keyj[z] ←keyj+1[z]
8 j ← j +1
9 if not leaf[z]
10 then cn[y]+1[y] ←c1[z]
11 j ← 1
12 while j <= n[z]+1
13 do cj[z] ←cj+1[z]
14 j ← j + 1
15 DISK-WRITE(y)
16 DISK-WRITE(z)
17 DISK-WRITE(x)
注意:每次递归调用前,程序都能保证包括关键字的子树根的关键字数至少为t(除了根结点外),
这是B-TREE-DELETE-NONONE子过程能够正确运行的关键,类似的,
可以用循环不变式证明B-TREE-DELETE-NONONE子过程的正确性。
————————————————————————————————————
【转自】http://blog.csdn.net/swordmanwk/article/details/6549480