第10章 kNN:推荐系统
k近邻算法(k-Nearest Neighbors, kNN):思路是,要预测某个点是哪一类,就看离它最近的k个点是哪一类,根据少数服从多数的原则预测目标点的类别。
代码实现:
#生成距离矩阵
distance.matrix <- function(df) {
#计算距离矩阵大小
distance <- matrix(rep(NA, nrow(df) ^ 2), nrow = nrow(df))
#计算欧氏距离并放入距离矩阵内
for (i in 1:nrow(df)) {
for (j in 1:nrow(df)) {
distance[i, j] <- sqrt((df[i, 'X'] - df[j, 'X']) ^ 2 + (df[i, 'Y'] - df[j, 'Y']) ^ 2)
}
}
return(distance)
}
#查找与目标距离最近的k个点
#注意最近的点是目标本身,因此从第2个点开始
k.nearest.neighbors <- function(i, distance, k = 5) {
return(order(distance[i, ])[2:(k + 1)])
}
#计算预测值
knn <- function(df, k = 5) {
distance <- distance.matrix(df)
predictions <- rep(NA, nrow(df))
for (i in 1:nrow(df)) {
indices <- k.nearest.neighbors(i, distance, k = k)
#prediction:最近k个点的Label均值,大于0.5设为1,否则为0
predictions[i] <- ifelse(mean(df[indices, 'Label']) > 0.5, 1, 0)
}
return(predictions)
}
应用算法:
#导入数据
df <- read.csv('ML_for_Hackers/10-Recommendations/data/example_data.csv')
#添加预测列
df <- transform(df, kNNPredictions = knn(df))
计算预测与实际不符的观测数与总观测数:

也就是说,准确率为93%
接下来用R语言中自带的knn算法和逻辑回归模型检验
rm('knn') # In case you still have our implementation in memory.
library('class')
df <- read.csv('ML_for_Hackers/10-Recommendations/data/example_data.csv')
n <- nrow(df)
set.seed(1)
indices <- sort(sample(1:n, n * (1 / 2)))
training.x <- df[indices, 1:2]
test.x <- df[-indices, 1:2]
training.y <- df[indices, 3]
test.y <- df[-indices, 3]
predicted.y <- knn(training.x, test.x, training.y, k = 5)
#sum(predicted.y != test.y)
#length(test.y)
logit.model <- glm(Label ~ X + Y, data = df[indices, ])
predictions <- as.numeric(predict(logit.model, newdata = df[-indices, ]) > 0)
#sum(predictions != test.y)


由此可以看出,当问题不能用线性模型来拟合的时候,k近邻算法的表现比较好。
R程序包推荐:根据一个程序员已经安装的程序包信息,来预测这个程序员是否会安装另一个程序包
installations <- read.csv('ML_for_Hackers/10-Recommendations/data/installations.csv')
library(reshape)
user.package.matrix <- cast(installations, User ~ Package, value = 'Installed')
#矩阵的第一列是用户ID,因此将其设置为row.name后删除
row.names(user.package.matrix) <- user.package.matrix[, 1]
user.package.matrix <- user.package.matrix[, -1]
similarities <- cor(user.package.matrix)
#nrow(similarities)
#ncol(similarities)
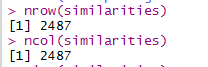
similarities表示相似度,最相似为1,最不相似为-1;而kNN算法需要将相似度转换为距离,最近为0,最远为无穷大
distances <- -log((similarities / 2) + 0.5)
使用最近邻信息,根据它的邻居有多少个已经被安装,来预测它会被安装的概率
installation.probability <- function(user, package, user.package.matrix, distances, k = 25) {
neighbors <- k.nearest.neighbors(package, distances, k = k)
return(mean(sapply(neighbors, function (neighbor) {user.package.matrix[user, neighbor]})))
}
installation.probability(1, 1, user.package.matrix, distances)
代码运行得到的值为0.76,即用户1有0.76的概率安装了程序包1
接下来,找到用户最可能安装的程序包,把它推荐给用户:
遍历所有程序包,分别计算它们被安装的概率,给出概率最大的那个。
most.probable.packages <- function(user, user.package.matrix, distances, k = 25) {
return(order(sapply(1:ncol(user.package.matrix),
function (package) {installation.probability(user, package, user.package.matrix, distances, k = k)}),
decreasing = TRUE))
}
user <- 1
listing <- most.probable.packages(user, user.package.matrix, distances)
colnames(user.package.matrix)[listing[1:10]]

这种推荐方式的解释是,因为用户已经安装了程序包X,Y,Z,所以他也有可能需要下一个安装包。这个推荐系统仅仅使用了相似性度量。