[读书笔记]机器学习：实用案例解析（12）

第12章 模型比较

SVM（支持向量机）简介

非线性决策边界问题：

df <- read.csv('ML_for_Hackers/12-Model_Comparison/data/df.csv')

ggplot(df) + geom_point(aes(x = X, y = Y, colour = factor(Label)))

#逻辑回归及评价预测准确率
logit.fit <- glm(Label ~ X + Y, family = binomial(link = 'logit'), data = df)
logit.predictions <- ifelse(predict(logit.fit) > 0, 1, 0)
mean(with(df, logit.predictions == Label))
#全部预测Label=0是的准确率
mean(with(df, Label == 0))

　　

支持向量机（SVM, Support Vector Machine）是由Vapnik等人根据统计学习理论中的结构风险最小化的原则提出的。^[2]支持向量机最初用于分类问题，是基于最大间隔准则得到的，通过求解一个二次凸规划问题得到一个极大间隔分类超平面，由此解决分类问题。用于回归问题时，就是将每个样本对应的标记记为连续实数，而非离散的标记。^[1] 

#SVM预测准确率
library(e1071)
svm.fit <- svm(Label ~ X + Y, data = df)
svm.prediction <- ifelse(predict(svm.fit) > 0, 1, 0)
mean(with(df, svm.prediction == Label))

#可视化对比两者预测结果
library(reshape)
df <- cbind(df, data.frame(Logit = ifelse(predict(logit.fit) > 0, 1, 0), 
                           SVM = ifelse(predict(svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, colour = factor(value))) + geom_point() + facet_grid(variable ~ .)

　　

支持向量机中需要选择核函数，通过将数据映射到高维空间，来解决大部分情况下，数据非线性可分的问题。核函数的选择是支持向量机中最重要的问题之一，目前并没有理论依据去直接选择，因此需要在实验中去尝试并调节各个核函数的核参数，直到找到表现最好的模型。不同的核函数对应的核参数的数目、取值和意义也有所差异。

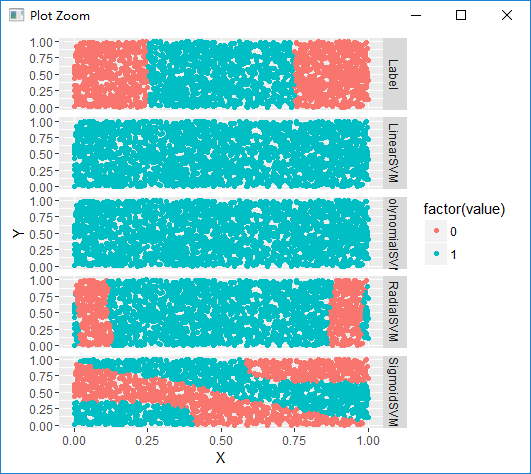
#SVM不同核函数之间的对比
df <- df[, c('X', 'Y', 'Label')]
linear.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'linear')
with(df, mean(Label == ifelse(predict(linear.svm.fit) > 0, 1, 0)))

polynomial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial')
with(df, mean(Label == ifelse(predict(polynomial.svm.fit) > 0, 1, 0)))

radial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial')
with(df, mean(Label == ifelse(predict(radial.svm.fit) > 0, 1, 0)))

sigmoid.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid')
with(df, mean(Label == ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))

df <- cbind(df, data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, 0), 
                           PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, 0), 
                           RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, 0), 
                           SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, colour = factor(value))) + geom_point() + facet_grid(variable ~ .)

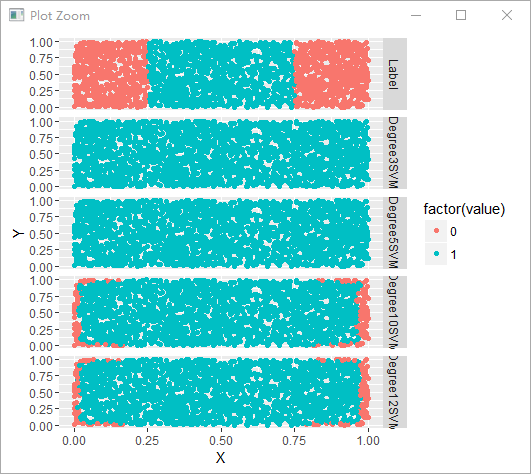
#不同degree下的多项式核函数分类结果比较
polynomial.degree3.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial', degree = 3)
with(df, mean(Label != ifelse(predict(polynomial.degree3.svm.fit) > 0, 1, 0)))

polynomial.degree5.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial', degree = 5)
with(df, mean(Label != ifelse(predict(polynomial.degree5.svm.fit) > 0, 1, 0)))

polynomial.degree10.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial', degree = 10)
with(df, mean(Label != ifelse(predict(polynomial.degree10.svm.fit) > 0, 1, 0)))

polynomial.degree12.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial', degree = 12)
with(df, mean(Label != ifelse(predict(polynomial.degree12.svm.fit) > 0, 1, 0)))

df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df, data.frame(Degree3SVM = ifelse(predict(polynomial.degree3.svm.fit) > 0, 1, 0),
                           Degree5SVM = ifelse(predict(polynomial.degree5.svm.fit) > 0, 1, 0),
                           Degree10SVM = ifelse(predict(polynomial.degree10.svm.fit) > 0, 1, 0),
                           Degree12SVM = ifelse(predict(polynomial.degree12.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) + geom_point() + facet_grid(variable ~ .)

#不同cost下的径向核函数分类结果比较
radial.cost1.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial', cost = 1)
with(df, mean(Label == ifelse(predict(radial.cost1.svm.fit) > 0, 1, 0)))

radial.cost2.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial', cost = 2)
with(df, mean(Label == ifelse(predict(radial.cost2.svm.fit) > 0, 1, 0)))

radial.cost3.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial', cost = 3)
with(df, mean(Label == ifelse(predict(radial.cost3.svm.fit) > 0, 1, 0)))

radial.cost4.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial', cost = 4)
with(df, mean(Label == ifelse(predict(radial.cost4.svm.fit) > 0, 1, 0)))

df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df, data.frame(Cost1SVM = ifelse(predict(radial.cost1.svm.fit) > 0, 1, 0),
                           Cost2SVM = ifelse(predict(radial.cost2.svm.fit) > 0, 1, 0),
                           Cost3SVM = ifelse(predict(radial.cost3.svm.fit) > 0, 1, 0),
                           Cost4SVM = ifelse(predict(radial.cost4.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) + geom_point() + facet_grid(variable ~ .)

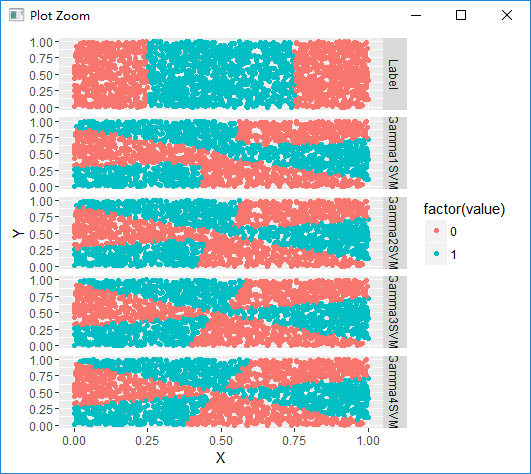
#不同gamma下的sigmoid核函数分类结果比较
sigmoid.gamma1.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid', gamma = 1)
with(df, mean(Label == ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0)))

sigmoid.gamma2.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid', gamma = 2)
with(df, mean(Label == ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0)))

sigmoid.gamma3.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid', gamma = 3)
with(df, mean(Label == ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0)))

sigmoid.gamma4.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid', gamma = 4)
with(df, mean(Label == ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))

df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df, data.frame(Gamma1SVM = ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0),
                           Gamma2SVM = ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0),
                           Gamma3SVM = ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0),
                           Gamma4SVM = ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) + geom_point() + facet_grid(variable ~ .)

　　

算法比较

在机器学习领域，一个菜鸟和一个专家之间的一个重要差别，就在于后者知道某些特定的问题不适合某些算法。为了培养一个机器学习领域专家那样的直觉，最好的办法就是，对你遇到的每一个机器学习问题，把所有的算法试个遍，知道有一天，你凭直觉就知道某些算法行不通。

以垃圾邮件的数据为例，对逻辑回归、SVM和kNN三种算法进行比较：

加载数据并分割训练集和测试集：

#载入数据
load('ML_for_Hackers/12-Model_Comparison/data/dtm.RData')
set.seed(1)
training.indices <- sort(sample(1:nrow(dtm), round(0.5 * nrow(dtm))))
test.indices <- which(! 1:nrow(dtm) %in% training.indices)
train.x <- dtm[training.indices, 3:ncol(dtm)]
train.y <- dtm[training.indices, 1]
test.x <- dtm[test.indices, 3:ncol(dtm)]
test.y <- dtm[test.indices, 1]
rm(dtm)

　　

逻辑回归：

#正则化的逻辑回归拟合
library(glmnet)
regularized.logit.fit <- glmnet(train.x, train.y, family = c('binomial'))
#模型优化：调节超参数lambda
#注意此处不是标准的交叉验证法，应该对每一次lambda都做一次训练集和测试集的分割
lambdas <- regularized.logit.fit$lambda
performance <- data.frame()
for (lambda in lambdas) {
  predictions <- predict(regularized.logit.fit, test.x, s = lambda)
  predictions <- as.numeric(predictions > 0)
  mse <- mean(predictions != test.y)
  performance <- rbind(performance, data.frame(Lambda = lambda, MSE = mse))
}
ggplot(performance, aes(x = Lambda, y = MSE)) + geom_point() + scale_x_log10()
best.lambda <- with(performance, max(Lambda[which(MSE == min(MSE))]))
mse <- with(subset(performance, Lambda == best.lambda), MSE)

　　

SVM：

#线性核函数
library('e1071')
linear.svm.fit <- svm(train.x, train.y, kernel = 'linear')
predictions <- predict(linear.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse
#径向核函数
radial.svm.fit <- svm(train.x, train.y, kernel = 'radial')
predictions <- predict(radial.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse

需要注意的一点是，比较模型之间的效果时，看到的模型的一部分效果，取决于在这个模型上花费的心血与时间。如果你在一个模型调优上花费的时间比另一个模型多，那么它们之间效果的部分差异，很可能正是因为你为那个模型所花费了更多的调优时间，而不是模型本身的优劣差异。

kNN模型：

#k = 50
library('class')
knn.fit <- knn(train.x, test.x, train.y, k = 50)
predictions <- as.numeric(as.character(knn.fit))
mse <- mean(predictions != test.y)
mse
#k = 5 ~ 50中使mse最低时
performance <- data.frame()
for (k in seq(5, 50, by = 5)) {
  knn.fit <- knn(train.x, test.x, train.y, k = k)
  predictions <- as.numeric(as.character(knn.fit))
  mse <- mean(predictions != test.y)
  performance <- rbind(performance, data.frame(K = k, MSE = mse))
}
best.k <- with(performance, K[which(MSE == min(MSE))])
best.mse <- with(subset(performance, K == best.k), MSE)
best.mse

经过以上对比，发现在垃圾邮件分类的问题上，经过超参数调优的正则化的逻辑回归模型表现最好。事实上，对于垃圾邮件分类这类问题，逻辑回归的效果的确更好。

处理机器学习问题的几点经验：

（1）面对实际数据集，应该尝试多个不同的算法；

（2）没有所谓通用的“最优”算法，“最优”取决于具体的问题；

（3）你的模型效果一方面取决于真实的数据结构，另一方面也取决于你为模型的超参数调优所付出的努力

 参考文献：

[1].常甜甜. 支持向量机学习算法若干问题的研究[D].西安电子科技大学,2010.

[2].BURGES C J C. A Tutorial on Support Vector Machines for Pattern Recognition [J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-67.